Większość uczniów szkół średnich, nawet tych startujących w konkursach i olimpiadach, rachunek prawdopodobieństwa kojarzy głównie z niezbyt porywającymi zadaniami typu: "Rzucamy 3 razy kostką. Oblicz prawdopodobieństwo zdarzenia, w którym...". Sytuacja zmienia się na studiach wyłącznie odrobinę, gdy dochodzą pojęcia zmiennej losowej i jej rozkładu czy wartości oczekiwanej. Repertuar poszerza się więc o zadania, w których trzeba znaleźć rozkład czy wartość oczekiwaną pewnej zmiennej losowej, ale dalej nie powoduje to u większości okrzyków zachwytu. Mówiąc krótko - rachunek prawdopodobieństwa przeciętnemu uczniowi czy studentowi nie kojarzy się z niczym fascynującym.

Jeżeli tak jest i w Twoim przypadku, Drogi Czytelniku, to ten artykuł jest właśnie dla Ciebie. Jego celem jest bowiem ukazanie zupełnie zaskakujących możliwości zastosowania rachunku prawdopodobieństwa w zagadnieniach, które nie tylko nie mają związku z żadnymi kostkami i monetami, a nawet nie ma w nich słowa o jakimkolwiek prawdopodobieństwie. Jedno z najbardziej typowych zastosowań metody probabilistycznej dotyczy sytuacji, w której chcemy udowodnić istnienie obiektu o pewnej żądanej własności. Często taki obiekt skonstruować jest bardzo trudno. Zamiast tego możemy udowodnić, że prawdopodobieństwo jego istnienia jest dodatnie! Brzmi to być może na tyle nieprawdopodobnie (!), że lepiej będzie zobaczyć to na przykładzie.

W tym przykładzie wyraźnie rzuca się w oczy bardzo istotna cecha metody probabilistycznej: za jej pomocą z reguły dowodzimy, że coś istnieje, ale nie wskazujemy tego. Ten schemat rozumowania w żadnym wypadku nie wyczerpuje jednak wszystkich jej możliwych zastosowań. Aby to zademonstrować, przyjrzyjmy się, jak korzystając z rachunku prawdopodobieństwa, można udowodnić równość dotyczącą wielokątów wypukłych, których wierzchołki znajdują się w ustalonym zbiorze punktów na płaszczyźnie.

W dalszych przykładach wykorzystamy pojęcia zmiennej losowej oraz jej wartości oczekiwanej. Precyzyjne definicje Czytelnik znajdzie bez problemu w Internecie lub w dowolnym podręczniku rachunku prawdopodobieństwa, a więc jedynie poglądowo przypomnimy znaczenie tych pojęć. Na zmienną losową możemy patrzeć jako na funkcję liczbową związaną z losowaniem. Na przykład rzucamy trzy razy kostką. Zmienną losową jest wówczas, powiedzmy, suma wyrzuconych oczek, iloczyn wyrzuconych oczek, liczba kostek, na których wypadła szóstka i tak dalej. Wartością oczekiwaną zmiennej losowej 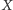jest jej wartość "średnia" - czyli jeżeli zmienna losowa 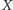przyjmuje wartość 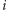z prawdopodobieństwem 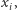to Nietrudno udowodnić, że wartość oczekiwana jest liniowa, tzn. dla dowolnych zmiennych losowych 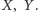Dla nas jest jeszcze istotna jej inna oczywista własność: zmienna losowa zawsze przyjmuje pewną wartość nie mniejszą (i pewną nie większą) niż jej wartość oczekiwana.

Na zakończenie rozważymy przykład o bardziej teorioliczbowym charakterze.

Chociaż metoda probabilistyczna słynie przede wszystkim ze swoich zastosowań w kombinatoryce, jej możliwości są dużo większe. Na stronie angielskiej Wikipedii zebrane zostały przykłady poważnych twierdzeń, które można udowodnić z użyciem rachunku prawdopodobieństwa. Lista jest doprawdy imponująca i zawiera przykłady z dziedziny analizy, algebry, teorii liczb czy nawet topologii. Do najbardziej fascynujących ilustracji tej metody na pewno można zaliczyć twierdzenie Weierstrassa o aproksymacji funkcji ciągłych wielomianami, które można udowodnić z użyciem tzw. prawa wielkich liczb. Bardzo intrygujący może być również dowód zasadniczego twierdzenia algebry z użyciem dwuwymiarowych ruchów Browna.

Metoda probabilistyczna nie jest jedynie kolejną techniką rozwiązywania zadań olimpijskich, a potężnym narzędziem stosowanym współcześnie w wielu działach matematyki. Bardzo duża część obecnie intensywnie badanej wielowymiarowej geometrii wypukłej opiera się na metodach losowych.

Czytelnik zainteresowany bardziej zaawansowanymi zastosowaniami tej metody może zajrzeć do doskonałej książki Nogi Alona i Joela H. Spencera: The Probabilistic Method oraz spróbować swoich sił w dwóch interesujących zadaniach pozostawionych do samodzielnego rozwiązania.