Przy grze dwuosobowej, w której gramy na pieniądze, można często określić oczekiwaną wartość rozgrywki. Jest to suma możliwych wyników ważona prawdopodobieństwami ich uzyskania. Załóżmy, że obliczenia wykonamy z punktu widzenia jednego z zawodników. Jeśli po odjęciu stawki, którą zapłacił, otrzymamy wartość dodatnią, to gracz ten będzie mniej więcej tyle średnio wygrywał, jeśli ujemną, to tyle będzie średnio przegrywał. Jeśli dodatkowo tak obliczona wartość oczekiwana okaże się skończona, to wyznaczając wartość oczekiwaną wypłaty otrzymamy stawkę graniczną: powyżej tej stawki nie opłaca się płacić za udział w grze, poniżej warto w taką grę wchodzić. Gdyby zaś wartość oczekiwana takiej gry okazała się nieskończona, to właśnie mielibyśmy do czynienia z paradoksem petersburskim.

W oryginalnym zadaniu, rozważanym jeszcze w XVIII w. przez Daniela Bernoulliego, z prawdopodobieństwem 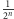wygrywaliśmy 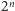zł. Łatwo sprawdzić, że wartość oczekiwana takiego rozkładu zmiennej losowej wynosi

Na pierwszy rzut oka wygląda to niewiarygodnie: w każdej grze wygrywamy przecież skończoną ilość pieniędzy. Jak więc można wygrać średnio nieskończenie wiele? Otóż nie można! Wyobrażanie sobie wartości oczekiwanej jako średniego wyniku było błędem. Jedyne, co nam pozostaje, to odwołać się do obliczonej wartości granicznej i przyjąć, że gdy jest ona nieskończona, to opłaca się w takiej grze postawić każdą sumę, aby tylko uzyskać możliwość zagrania. Gdy przyjrzano się temu fenomenowi bliżej, okazało się, że ludzie w to nie wierzą i nie są skłonni do aż takiego hazardu. W badaniu ankietowym, opisanym na początku lat 80. XX wieku, deklarowana średnia wartość, którą ankietowani byli skłonni postawić w grze Bernoulliego wynosiła 25 zł. To zastanawiające: czyżbyśmy aż tak nie wierzyli w matematykę? Czyżby nasze intuicje były zbyt dalekie od rzeczywistości? Może po prostu kłania się zwykła, a jakże powszechna ignorancja matematyczna? Niewykluczone też, że w końcu istnieje jeszcze jakiś inny powód.

Przyjrzyjmy się bliżej możliwym przyczynom takiej nieufności. Pamiętajmy, że warunkiem uzyskania nieskończonej wartości oczekiwanej jest pełna wypłacalność naszego przeciwnika. Jeśli jego zasoby pieniężne są ograniczone, to deklaruje on, że gra nie może trwać dłużej niż jakaś z góry ustalona liczba rzutów. Oznacza to, że jeśli na przykład ustalimy, że rzutów nie może być więcej niż 10, to partner wypłaci nam co najwyżej 1024 zł. W tym przypadku najdalej po 9 rzutach już będziemy znali wynik gry. Jeśli wypadnie kolejno 9 reszek, to już możemy nie wykonywać ostatniego rzutu monetą, gdyż wtedy i tak dostaniemy tę maksymalną stawkę wynikającą z przyjętego ograniczenia. Cały paradoks jednak wtedy znika. Niezależnie od wysokości deklarowanego limitu rzutów, wartość oczekiwana wypłaty staje się skończona. Bez trudu więc możemy wyznaczyć graniczną wartość, do wysokości której opłaca się wejść do gry. Załóżmy więc ogólnie, że gramy w grę Bernoulliego za pomocą monety: rzucamy tak długo, aż wypadnie orzeł. Liczymy liczbę 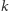reszek, które wcześniej wypadły, a nasz przeciwnik wypłaca nam tyle złotych, ile wynosi dwa podniesione do liczby wykonanych rzutów, czyli 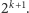Gdy maksymalna liczba reszek zostanie ustalona na 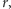wówczas wartość oczekiwana naszej wygranej wynosi

Pierwsze składników tej sumy odpowiada wypadnięciom kolejno zera reszek, jednej reszki, dwóch reszek, 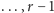reszek. Ostatni składnik zbiera resztę przypadków. Załóżmy też, dla uproszczenia rachunków, że nasz przeciwnik dysponuje kwotą 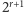i tyle właśnie oferuje nam jako maksymalną wypłatę. Wtedy, zgodnie z przeprowadzonymi rachunkami, graniczną wartością, która ustala stan równowagi gry jest 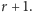Każdą kwotę mniejszą opłaca się postawić, większej się nie opłaca, a postawienie dokładnie tej kwoty jest neutralne: średnio nic nie zyskamy ani nie stracimy.

No cóż - widać, że grając z partnerem dysponującym kwotą będącą potęgą dwójki, warto wnieść do gry co najwyżej tyle pieniędzy, ile wynosi wykładnik tej potęgi, czyli logarytm dwójkowy z deklarowanej przez niego wartości. Widać też, że dla wartości niebędących potęgami dwójki to też będzie zależność logarytmiczna - w końcu mała różnica w obliczeniach dotyczy tylko ostatniego wyrazu. Wynik ten oznacza jednak, że wcale tak dużo nie powinniśmy być skłonni wydawać. Funkcja logarytmiczna, choć dąży do nieskończoności, to rośnie przecież bardzo wolno. Widzimy na przykład, że przeciwko partnerowi oferującemu co najwyżej 1024 zł nie powinniśmy stawiać więcej niż 10 zł. To jest jeszcze dość intuicyjne. Ale nawet jeśli stanie naprzeciw nas Bill Gates ze swoim majątkiem szacowanym na około 70 miliardów dolarów i powie, że gra z nami, gwarantując naszą wygraną wszystkim, co posiada (no może niech to będzie czyli 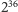dolarów dla łatwego rachunku - niech już Bill tak bardzo nie ryzykuje i coś sobie jednak zostawi w razie konieczności wypłaty wszystkiego, co zadeklarował), to nam opłacałoby się postawić w takiej grze zaledwie 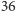dolarów! Idźmy dalej. Gdyby postawić wszystkie pieniądze znajdujące się w obiegu na świecie, a ich ilość szacuje się na mniej więcej 3 biliardy dolarów 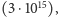wówczas nadal kwota równowagi nie byłaby imponująca - plasowałaby się w okolicy 50 dolarów. Swoją drogą śmiesznie byłoby wygrać całą pulę w takiej grze i stać się właścicielem wszystkich pieniędzy w obiegu światowym! Cóż - prawdopodobieństwo, że cały świat byłby zainteresowany zagraniem w taką grę jest chyba jeszcze mniejsze niż szansa wygranej, nawet jak dorzucimy jeszcze z 5 dolarów na zachętę.

Widać więc, że ludzie ankietowani we wspomnianym badaniu wcale nie byli tacy głupi. Nawet byliby skłonni nieco przepłacić: kwota 25 dolarów odpowiada limitowi ponad 33 milionów. Szansa tak dużej wygranej to jeden do ponad 16 milionów. Mniej niż trafienie szóstki w totolotka, więc naprawdę trzeba by długo grać, żeby trafić taką sumę. Po prostu badani mieli zdrowe wyczucie nieskończoności, która, choć duża, to w realnym świecie przecież nie istnieje. Ciekawe, że matematyka, którą Hermann Weyl nazwał (a wielu matematyków podziela ten pogląd) nauką o nieskończoności, jest badaniem rzeczy tak bardzo niewystępujących w przyrodzie, a nasze intuicje są często dalekie od tego, co myślą o tym matematycy.