Tak bardzo oczekiwana wartość
Nazywano ją kiedyś nadzieją. Czasami dodawano przymiotnik „matematyczna”, żeby nie było nieporozumień. Chodziło bowiem o wartość oczekiwaną, czyli o pojęcie znane z rachunku prawdopodobieństwa. Słowo nadzieja faktycznie budziło wątpliwości, szczególnie gdy mierzono jakieś negatywnie nacechowane wielkości, jak liczba zgonów, wypadków samochodowych czy strat. Powiedzenie „nadzieja, jeśli chodzi o wysokość straty, wynosi 100 zł” brzmi zupełnie inaczej niż „wartość oczekiwana straty to 100 zł”.
Ze szkoły znamy zapewne ciekawy przypadek rzutu kostką: średnio wypada
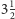 oczka. Każdy wynik ważymy bowiem prawdopodobieństwem,
z jakim się go spodziewamy – tu wszystkie prawdopodobieństwa
wynoszą
oczka. Każdy wynik ważymy bowiem prawdopodobieństwem,
z jakim się go spodziewamy – tu wszystkie prawdopodobieństwa
wynoszą
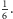 Łącznie mamy więc
Łącznie mamy więc

Ale widział kto kiedy kostkę, która tyle właśnie pokazuje? Okazuje się, że ta
„typowa” wartość jest w ogóle niemożliwa. Choć jeśli wykonamy
odpowiednio dużo doświadczeń i obliczymy średnią z wyników rzutów,
to wyjdzie nam coś w okolicy
Właściwie można powiedzieć, że pojęcie wartości oczekiwanej było obecne u zarania, kiedy powstawał rachunek prawdopodobieństwa. Do Błażeja Pascala zgłosił się jego znajomy, Antoni Gombaud, lepiej znany jako kawaler de Méré, z prośbą, aby rozstrzygnąć sposób podziału puli pieniędzy przy grze w kości, gdy przerwie się grę w momencie, kiedy jedna ze stron wygrywa. W skrócie rzecz biorąc, możemy założyć, że mamy prostą grę, w której z zadanym prawdopodobieństwem, przyjmijmy roboczo że 50%, jeden z graczy wygrywa. Na przykład, gracze rzucają na przemian kośćmi i rundę wygrywa ten, kto pierwszy wyrzuci parę szóstek. Pięć wygranych rund oznacza wygraną całego meczu i, niezależnie od tego, ile punktów zdobył przeciwnik, zgarnia się całą pulę.
Kawaler de Méré zadał Pascalowi pytanie, jak należało pulę podzielić, gdy jego przeciwnik miał 3, a on sam 4 punkty i grę musiano przerwać. Przeciwnik uważał, że w stosunku 3 do 4, czyli zgodnie z liczbą zdobytych punktów. Kawaler de Méré, że w stosunku 1 do 2, gdyż do wygranej jemu brakowało tylko jednego punktu, podczas gdy przeciwnikowi aż dwóch. Pascal przeprowadził rozumowanie, które dla nas dziś jest oczywiste: w połowie przypadków kolejną rundę, a zatem cały mecz wygra kawaler de Méré, a z pozostałej połowy znów połowę stanowi szansa wygrania przez niego całego meczu. Zatem łącznie kawaler de Méré miał aż trzy szanse na cztery, że wygra, podczas gdy jego przeciwnik tylko jedną. Pulę więc należałoby podzielić w stosunku 1 do 3. Zatem ani de Méré, ani jego partner nie mieli racji.
W rzeczywistości kawaler de Méré był zainteresowany innymi, bardziej złożonymi zagadnieniami. Chodziło mu o wyznaczenie takiej liczby rzutów, aby szanse na wygraną przekraczały połowę – wtedy mógł się zakładać na równych zasadach. Empirycznie doszedł, na przykład, do tego, że opłaca mu się przyjąć zakład o to, iż przy 4 rzutach kostką wypadnie co najmniej jedna szóstka. W rzeczywistości prawdopodobieństwo tego zdarzenia to prawie 52%. Nieco trudniej poszło mu z wyznaczeniem najmniejszej opłacalnej liczby rzutów dwiema kostkami tak, aby można się było założyć na równe stawki o to, że wypadną w końcu jednocześnie 2 szóstki. Wyszło mu 24, choć – jak się łatwo możemy dziś przekonać – musiał popełnić błąd (albo też miał nieco zwichnięte kości), gdyż prawdopodobieństwo sukcesu wynosi tu około 0,4914 i dopiero 25 rzutów daje przewagę. Pascal skontaktował się z innym francuskim matematykiem, Piotrem Fermatem. W rezultacie ich wspólnych dociekań powstała wymiana listów o zawartości, która uzasadnia stwierdzenie, że właśnie wtedy powstała teoria prawdopodobieństwa.
Zmienna losowa – wynalazek nieco późniejszy – to po prostu kodowanie
niektórych wyników za pomocą liczb. Na przykład możemy kodować
sukces przez wartość 1, a porażkę przez wartość 0. Jeżeli znamy
prawdopodobieństwo sukcesu
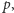 to możemy się spodziewać, że
średnio w
to możemy się spodziewać, że
średnio w
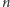 doświadczeniach losowych uzyskamy
doświadczeniach losowych uzyskamy
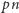 jedynek
i
jedynek
i
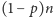 zer. Wartość oczekiwana takiej dyskretnej zmiennej losowej
to po prostu ważona odpowiednimi prawdopodobieństwami suma jej
możliwych wyników.
zer. Wartość oczekiwana takiej dyskretnej zmiennej losowej
to po prostu ważona odpowiednimi prawdopodobieństwami suma jej
możliwych wyników.
Problem kawalera de Méré możemy ściśle ująć następująco.
Przyjmijmy, że
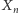 jest taką rodziną zmiennych losowych, że dla
ustalonego
jest taką rodziną zmiennych losowych, że dla
ustalonego
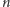 wartość zmiennej
wartość zmiennej
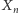 jest równa 1, jeśli
w
jest równa 1, jeśli
w
 kolejnych rzutach dwiema kośćmi wypadną co najmniej
dwie szóstki, a 0 – jeśli nie. Pytamy się teraz o to, dla jakiego
najmniejszego
kolejnych rzutach dwiema kośćmi wypadną co najmniej
dwie szóstki, a 0 – jeśli nie. Pytamy się teraz o to, dla jakiego
najmniejszego
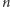 wartość oczekiwana
wartość oczekiwana
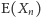 przekracza
połowę. Jeśli zatem będziemy w stanie wyznaczać wartości oczekiwane
przekracza
połowę. Jeśli zatem będziemy w stanie wyznaczać wartości oczekiwane
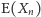 dla każdego
dla każdego
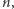 to zadanie to zostanie rozwiązane
i wynikiem jego będzie wartość
to zadanie to zostanie rozwiązane
i wynikiem jego będzie wartość
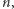 począwszy od której warto
się zakładać o to, że dwie szóstki wypadną jednocześnie w ciągu
począwszy od której warto
się zakładać o to, że dwie szóstki wypadną jednocześnie w ciągu
 rzutów.
rzutów.
Ogólnie, jeśli prawdopodobieństwo jakiegoś zdarzenia wynosi
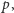 a sami
mamy nutkę hazardzisty oraz chętnego przeciwnika do zabawy, to mamy prostą
strategię zakładania się o to, że to właśnie zdarzenie nastąpi. Załóżmy, że
nasz przeciwnik jest skłonny wyłożyć pewną kwotę na zakład, iż nie uda
się nam nasze doświadczenie. Postarajmy się ustalić tak nasz udział
w zakładzie, aby się nam opłaciło. Dla uproszczenia przyjmijmy, że cała pula
po wpłaceniu przez nas stawek ma wartość 1. Ile zatem bylibyśmy
skłonni postawić w takim zakładzie? Oznaczmy tę niewiadomą stawkę
przez
a sami
mamy nutkę hazardzisty oraz chętnego przeciwnika do zabawy, to mamy prostą
strategię zakładania się o to, że to właśnie zdarzenie nastąpi. Załóżmy, że
nasz przeciwnik jest skłonny wyłożyć pewną kwotę na zakład, iż nie uda
się nam nasze doświadczenie. Postarajmy się ustalić tak nasz udział
w zakładzie, aby się nam opłaciło. Dla uproszczenia przyjmijmy, że cała pula
po wpłaceniu przez nas stawek ma wartość 1. Ile zatem bylibyśmy
skłonni postawić w takim zakładzie? Oznaczmy tę niewiadomą stawkę
przez
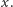 Wtedy z prawdopodobieństwem
Wtedy z prawdopodobieństwem
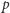 wygramy
wygramy
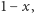 a z prawdopodobieństwem
a z prawdopodobieństwem
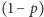 stracimy
stracimy
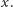 Chodzi
o to, żeby bilans wyszedł dodatni, zatem mamy nierówność
Chodzi
o to, żeby bilans wyszedł dodatni, zatem mamy nierówność
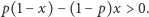 Rozwiązując ją, otrzymujemy po prostu
Rozwiązując ją, otrzymujemy po prostu
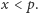 Zatem jeśli postawimy mniej niż
Zatem jeśli postawimy mniej niż
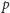 -tą część puli
przeciw
-tą część puli
przeciw
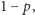 wyjdziemy na tym dobrze, jeśli więcej, to wyjdziemy
na tym źle, a jeśli postawimy dokładnie
wyjdziemy na tym dobrze, jeśli więcej, to wyjdziemy
na tym źle, a jeśli postawimy dokładnie
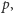 to zakład nie będzie
faworyzował nikogo z nas. Przy długich seriach wygrana będzie oscylowała
wokół zera.
to zakład nie będzie
faworyzował nikogo z nas. Przy długich seriach wygrana będzie oscylowała
wokół zera.
Sytuacja się komplikuje, jeżeli wygrane są duże w porównaniu do
prawdopodobieństw. Wyobraźmy sobie takie doświadczenie. Nasz kolega
bierze dwie identyczne puszki, monetę i trochę gotówki i wychodzi
do sąsiedniego pokoju. Tam rzuca monetą tak długo, aż wypadnie reszka.
Notuje liczbę wykonanych rzutów
 i do jednej puszki wkłada
i do jednej puszki wkłada
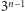 zł, a do drugiej
zł, a do drugiej
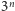 zł. Zamyka puszki, przynosi je nam
i proponuje, żebyśmy wybrali, z której puszki chcemy dostać pieniądze.
Możemy jedną z nich otworzyć i przeliczyć gotówkę, a następnie albo ją
wziąć, lub też „w ciemno” zdecydować się na drugą puszkę i zadowolić
tym, co tam zastaniemy. Jaką strategię powinniśmy przyjąć?
zł. Zamyka puszki, przynosi je nam
i proponuje, żebyśmy wybrali, z której puszki chcemy dostać pieniądze.
Możemy jedną z nich otworzyć i przeliczyć gotówkę, a następnie albo ją
wziąć, lub też „w ciemno” zdecydować się na drugą puszkę i zadowolić
tym, co tam zastaniemy. Jaką strategię powinniśmy przyjąć?
Zauważmy, że uzyskanie
 rzutów monetą do pierwszej reszki ma
prawdopodobieństwo
rzutów monetą do pierwszej reszki ma
prawdopodobieństwo
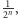 bo musi wypaść dokładnie
bo musi wypaść dokładnie
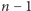 orłów,
a potem reszka. Jeśli widzimy, że w pierwszej puszce jest
orłów,
a potem reszka. Jeśli widzimy, że w pierwszej puszce jest
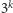 zł, to
albo
zł, to
albo
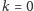 (czyli widzimy jedną złotówkę) i wtedy na pewno
opłaca się zdecydować na pewne
(czyli widzimy jedną złotówkę) i wtedy na pewno
opłaca się zdecydować na pewne
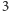 zł w drugiej puszce, albo
zł w drugiej puszce, albo
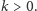 W tym drugim przypadku jeśli zdecydujemy się na pozostanie
przy pieniądzach z pierwszej puszki, to wygramy po prostu
W tym drugim przypadku jeśli zdecydujemy się na pozostanie
przy pieniądzach z pierwszej puszki, to wygramy po prostu
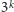 zł. Jeśli
natomiast zdecydujemy się na zmianę puszki, to możemy tam zastać
albo
zł. Jeśli
natomiast zdecydujemy się na zmianę puszki, to możemy tam zastać
albo
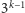 zł, albo
zł, albo
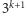 zł, przy czym to drugie zdarzenie
będzie dwa razy mniej prawdopodobne. Para
zł, przy czym to drugie zdarzenie
będzie dwa razy mniej prawdopodobne. Para
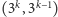 ma
bowiem prawdopodobieństwo
ma
bowiem prawdopodobieństwo
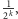 zaś para
zaś para
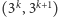 ma
prawdopodobieństwo
ma
prawdopodobieństwo
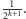 Zatem oczekiwana ilość pieniędzy
w drugiej puszce to
Zatem oczekiwana ilość pieniędzy
w drugiej puszce to
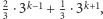 co jest większe niż
co jest większe niż
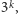 bo
przecież już sam drugi składnik to dokładnie
bo
przecież już sam drugi składnik to dokładnie
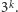

Dochodzimy do zaskakującego wniosku: zawsze się opłaca wybrać tę drugą puszkę! Ale po co w takim razie w ogóle było otwierać tę pierwszą? I która miałaby niby być ta pierwsza – przecież puszki są nierozróżnialne. Gdybyśmy chwycili najpierw tę drugą i przeliczyli pieniądze, które się tam znajdują, to też opłacałoby się zmienić decyzję? I uzyskać ostro większą wartość oczekiwaną przy zmianie decyzji z powrotem na tę pierwszą? Coś tu nie gra!
Dochodzimy tu do fenomenu znanego w probabilistyce pod nazwą paradoksu petersburskiego. Odkryty on został przez Daniela Bernoulliego. Odkrył on, że jeśli prawdopodobieństwa nieskończenie wielu zdarzeń będą odpowiednio duże, to wartość oczekiwana może wyjść nieskończona, mimo że w każdym doświadczeniu zyskujemy jedynie skończoną wartość. Tak jest i u nas. Nawet jeśli będziemy wybierali za każdym razem pierwszą puszkę, to wartość oczekiwana wyniesie co najmniej

A jak będziemy kaprysili i zdecydujemy się na branie tej drugiej puszki, to nawet więcej. Zaraz, zaraz. Więcej niż nieskończoność? O ile?
No właśnie! Nieskończoności nie da się przeskoczyć. Tu mamy do czynienia z nieintuicyjnym pojęciem nieskończonej wartości oczekiwanej. W ujęciu bliskim kawalerowi de Méré po prostu mamy do czynienia z sytuacją, w której zapytani, jaką sumę bylibyśmy w stanie zapłacić, aby w taką grę sobie zagrać, powinniśmy odpowiedzieć: każdą.
Ciekawe, że gdy psychologowie badali ten aspekt, okazało się, że ludzie nie byli tacy przekonani o opłacalności takiej gry i średnio deklarowali kilkadziesiąt zł.
Warto dodać, że Pascal pojęcie nieskończonej wartości oczekiwanej rozumiał na wiele lat przed Bernoullim. Oparł na nim swój słynny zakład. W obliczu nieskończonej szczęśliwości w przyszłym życiu oferowanej przez Boga nie należy kombinować, tylko po prostu żyć zgodnie z przykazaniami. Żadna wartość w doczesnym, skończonym życiu nie zrekompensuje nam braku wiecznego szczęścia. Nie mówiąc już o nieskończonej ujemnej wartości oczekiwanej, jeśli przydarzyłoby się nam przegrać na Sądzie Ostatecznym. Zostawmy może te rozważania teologom, a na własny użytek raczej omijajmy kolektury Lotto, bo tam oczekiwana wartość wygranej oscyluje wokół -50% opłaconej stawki. Więc jeśli nachodzi nas chęć wykupienia losu za 3 zł, to znacznie bardziej opłacalne jest wyrzucenie do kosza przy kolekturze, na przykład, złotówki. W długiej perspektywie wyjdziemy na tej strategii lepiej.
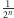 wygrywało się
wygrywało się
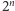 zł.
Łatwo sprawdzić, że wartość oczekiwana jest tu też nieskończona.
W opisywanym doświadczeniu średnia wartość deklarowanej stawki
do zaakceptowania przez pytanych wyniosła 25. [Ian Hacking, Strange
expectations, Philosophy of Science 47 (1980), nr 4, 562–567.]
zł.
Łatwo sprawdzić, że wartość oczekiwana jest tu też nieskończona.
W opisywanym doświadczeniu średnia wartość deklarowanej stawki
do zaakceptowania przez pytanych wyniosła 25. [Ian Hacking, Strange
expectations, Philosophy of Science 47 (1980), nr 4, 562–567.]