Szczęście w zbiorach mierzalnych
Wyobraźmy sobie następującą grę. Mamy planszę o polach ponumerowanych od 0 do 100 i dwa pionki, stojące na początku na polu o numerze 0. Gracze wykonują ruchy na przemian. Gracz rzuca monetą i jeśli wypadnie reszka, to przesuwa swój pionek o 1 pole, a jeśli orzeł – o 5 pól. Wygrywa ten, kto pierwszy dojdzie do pola o numerze 100.
Mało ciekawa gra, prawda? Zależy tylko od szczęścia, a nie od podejmowania słusznych decyzji. Dodajmy więc do niej jakiś element decyzyjny. Powiedzmy, że przed wykonaniem ruchu gracz może wybrać spośród dwóch wariantów: A i B. Jeśli wybierze wariant A, to rzuca monetą i wykonuje ruch tak, jak napisano wyżej.
Jeśli wybierze bardziej ryzykowny wariant B, to w przypadku wyrzucenia orła rusza się do przodu o 20 pól, ale w przypadku wyrzucenia reszki wraca na pole zerowe. Żeby nasza gra zawsze się kończyła, przyjmijmy, że jeśli 10 razy danemu graczowi wypadnie reszka podczas stosowania wariantu B, to ten gracz przegrywa.
Ta gra jest trochę ciekawsza (są sytuacje, w których bardziej opłaca się zastosować wariant A, i sytuacje, w których lepszy jest wariant B), ale wciąż zależy od szczęścia. No ale co to jest szczęście? Może dałoby się jakoś włączyć szczęście do samej gry, tak, żeby było deterministycznym elementem gry, a nie losowym?
Przyjmijmy, że nasze szczęście jest liczbą z przedziału
 (Szczęście
zawsze rozpatrujemy z punktu widzenia konkretnego gracza – jeśli
nasze szczęście jest równe
(Szczęście
zawsze rozpatrujemy z punktu widzenia konkretnego gracza – jeśli
nasze szczęście jest równe
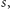 to szczęście przeciwnika wynosi
to szczęście przeciwnika wynosi
 ) Szczęście równe 1 oznaczałoby, że na monecie zawsze
będzie wypadało to, co chcemy. Szczęście równe 0 oznacza, że zawsze
wypada to, czego chce przeciwnik. Pośrednie wartości oznaczają, że obaj
gracze mają coś do powiedzenia. Przykładowo, jeśli szczęście jest
większe niż
) Szczęście równe 1 oznaczałoby, że na monecie zawsze
będzie wypadało to, co chcemy. Szczęście równe 0 oznacza, że zawsze
wypada to, czego chce przeciwnik. Pośrednie wartości oznaczają, że obaj
gracze mają coś do powiedzenia. Przykładowo, jeśli szczęście jest
większe niż
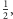 to powinniśmy mieć możliwość wybrania
wyniku rzutu monetą, ale będzie się to działo kosztem naszego szczęścia
w dalszej części gry.
to powinniśmy mieć możliwość wybrania
wyniku rzutu monetą, ale będzie się to działo kosztem naszego szczęścia
w dalszej części gry.
Dokładniej, szczęście działa w następujący sposób. Powiedzmy, że nasze
szczęście w pewnym momencie jest równe
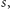 a reguły gry z elementem
losowym mówią, że powinniśmy w tym momencie rzucić monetą. Zamiast
to robić, decydujemy, jak podzielić
a reguły gry z elementem
losowym mówią, że powinniśmy w tym momencie rzucić monetą. Zamiast
to robić, decydujemy, jak podzielić
 między oba możliwe
wyniki. Wybieramy dwie liczby,
między oba możliwe
wyniki. Wybieramy dwie liczby,
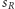 i
i
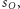 obie z przedziału
obie z przedziału
 i takie, że ich średnia jest równa
i takie, że ich średnia jest równa
 Przeciwnik
wybiera wynik rzutu – jeśli wybierze reszkę, to nasze szczęście zmienia
się na
Przeciwnik
wybiera wynik rzutu – jeśli wybierze reszkę, to nasze szczęście zmienia
się na
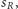 w przeciwnym przypadku nasze szczęście zmienia
się na
w przeciwnym przypadku nasze szczęście zmienia
się na
 Nie wolno mu wybrać takiego wyniku, któremu
przypisaliśmy wartość naszego szczęścia 1. Zauważmy, że dla
każdego rzutu monetą to my wybieramy podział
Nie wolno mu wybrać takiego wyniku, któremu
przypisaliśmy wartość naszego szczęścia 1. Zauważmy, że dla
każdego rzutu monetą to my wybieramy podział
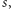 a przeciwnik
wybiera wynik rzutu, niezależnie od tego, do którego z graczy należał
rzut monetą.
a przeciwnik
wybiera wynik rzutu, niezależnie od tego, do którego z graczy należał
rzut monetą.
Przykładowo, wyobraźmy sobie taką prostą grę: gracze rzucają monetą
na przemian, zaczyna przeciwnik, a wygrywa ten, kto wyrzuci orła.
Zacznijmy ze szczęściem
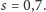 Gramy w następujący sposób:
w pierwszym ruchu przyporządkowujemy
Gramy w następujący sposób:
w pierwszym ruchu przyporządkowujemy
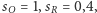 dzięki czemu
blokujemy przeciwnikowi orła i „wypada reszka”, ale nasze szczęście spada
do
dzięki czemu
blokujemy przeciwnikowi orła i „wypada reszka”, ale nasze szczęście spada
do
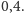 Teraz, oczywiście, przeciwnik nie wybierze orła (bo jest
nasz ruch), także możemy mu przypisać dowolnie małą wartość
szczęścia i przyporządkowujemy
Teraz, oczywiście, przeciwnik nie wybierze orła (bo jest
nasz ruch), także możemy mu przypisać dowolnie małą wartość
szczęścia i przyporządkowujemy
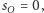
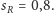 Wypada
reszka, nasze szczęście wzrosło do
Wypada
reszka, nasze szczęście wzrosło do
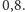 Po wymuszeniu reszki
w ten sam sposób, co ostatnio, szczęście spada do
Po wymuszeniu reszki
w ten sam sposób, co ostatnio, szczęście spada do
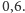 Teraz
możemy przyporządkować
Teraz
możemy przyporządkować
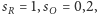 zatem wypada orzeł
i wygrywamy. Można pokazać, że wygrywamy dla wartości szczęścia
powyżej
zatem wypada orzeł
i wygrywamy. Można pokazać, że wygrywamy dla wartości szczęścia
powyżej
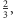 dla wartości poniżej
dla wartości poniżej
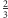 wygrywa przeciwnik (dla
wygrywa przeciwnik (dla
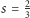 gra się nie skończy, a właściwie skończy się wtedy, gdy któryś
z graczy się znudzi i wykona ruch prowadzący do zakończenia gry
jego przegraną).
gra się nie skończy, a właściwie skończy się wtedy, gdy któryś
z graczy się znudzi i wykona ruch prowadzący do zakończenia gry
jego przegraną).
Co właściwie oznacza szczęście? Jeśli gra jest skończona (na przykład w powyższej grze uznajemy, że jeśli po 100 rzutach nie doszło do konkluzji, to następny rzut decyduje), to można udowodnić, że jeśli w danym momencie szczęście jest większe od prawdopodobieństwa wygrania gry losowej przez przeciwnika (przy założeniu, że obaj gracze stosują optymalne strategie), to my mamy strategię wygrywającą. Jeśli jest mniejsze, to strategię wygrywającą ma przeciwnik. Strategia polega na tym, by wszystkie sytuacje, w których nie mamy szans wygrać, blokować (korzystając z wysokiej wartości szczęścia), a w pozostałych grać tak, by powyższy warunek był zachowany (szczęście ma być zawsze większe niż prawdopodobieństwo). Szczegóły dowodu zostawiamy Czytelnikowi. Polecamy też się zastanowić, jak dostosować ten system do popularnych gier z użyciem kostki, od (dwuosobowego) chińczyka do backgammona. Albo do gier, w których ważny jest wynik (a nie tylko, kto wygrał, a kto przegrał), lub też do gier, w których losowość wynika stąd, że obaj gracze podejmują decyzje jednocześnie (jak kamień-nożyce-papier). Zauważmy również, że gra ma niesymetryczny charakter, bo mamy dwóch graczy: gracz wybierający podział („dzielący”) i gracz wybierający wynik rzutu („rządzący”). Te dwie role mogą być na stałe przypisane do graczy, można też się zastanowić nad systemem, w którym role się zmieniają.
W powyższej grze zarządziliśmy, żeby rozgrywka zawsze była skończona.
Jednak można wymyślić gry, w których rozgrywka czasami albo zawsze jest
nieskończona. W przypadku rozgrywek nieskończonych również w jakiś
sposób określamy zwycięzcę. Przykład takiej gry nieskończonej? Mamy
pewien podzbiór
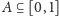 i dwa pionki, z których jeden stawiamy
w punkcie 0, a drugi w punkcie 1. Gracze na przemian wybierają jeden
z pionków i stawiają go w punkcie dokładnie pośrodku pomiędzy
poprzednimi pozycjami pionków. Tak więc w pierwszym ruchu my
przestawiamy jeden z pionków do punktu
i dwa pionki, z których jeden stawiamy
w punkcie 0, a drugi w punkcie 1. Gracze na przemian wybierają jeden
z pionków i stawiają go w punkcie dokładnie pośrodku pomiędzy
poprzednimi pozycjami pionków. Tak więc w pierwszym ruchu my
przestawiamy jeden z pionków do punktu
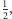 powiedzmy ten,
który wcześniej stał w 1, a w drugim ruchu przeciwnik wybiera, który
z pionków ma przenieść do punktu
powiedzmy ten,
który wcześniej stał w 1, a w drugim ruchu przeciwnik wybiera, który
z pionków ma przenieść do punktu
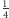 (średnia 0 i
(średnia 0 i
 ). Jeśli
wybrał przestawienie pionka z 0, to my przestawiamy jeden z pionków
do
). Jeśli
wybrał przestawienie pionka z 0, to my przestawiamy jeden z pionków
do
 i tak dalej. „Po nieskończonym czasie” oba pionki będą
stały w tym samym punkcie granicznym. Jeśli ten punkt graniczny należy
do zbioru
i tak dalej. „Po nieskończonym czasie” oba pionki będą
stały w tym samym punkcie granicznym. Jeśli ten punkt graniczny należy
do zbioru
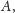 to my wygrywamy, jeśli nie, to wygrywa przeciwnik.
Można pokazać np. że jeśli zbiór
to my wygrywamy, jeśli nie, to wygrywa przeciwnik.
Można pokazać np. że jeśli zbiór
 jest zbiorem liczb wymiernych,
to w takiej grze nieskończonej przeciwnik ma strategię wygrywającą (chociaż
w skończonej grze pionki zawsze będą stały na liczbach wymiernych) –
strategia ta polega na tym, że przeciwnik ustawia wszystkie liczby wymierne
w ciąg, i w kolejnych swoich ruchach dba o to, żeby wykluczać kolejne liczby
z tego ciągu jako możliwe punkty graniczne.
jest zbiorem liczb wymiernych,
to w takiej grze nieskończonej przeciwnik ma strategię wygrywającą (chociaż
w skończonej grze pionki zawsze będą stały na liczbach wymiernych) –
strategia ta polega na tym, że przeciwnik ustawia wszystkie liczby wymierne
w ciąg, i w kolejnych swoich ruchach dba o to, żeby wykluczać kolejne liczby
z tego ciągu jako możliwe punkty graniczne.
W powyższej grze wybory „świadome” można zastąpić wyborami
losowymi (pionek przenoszony do środka wybieramy losowo). Wtedy punkt
graniczny jest wybierany całkowicie losowo, zatem prawdopodobieństwo, że
my wygramy, jest równe prawdopodobieństwu, że losowo wybrany punkt
należy do zbioru
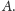
Czy podany wyżej sposób na zamianę gry losowej na grę deterministyczną
„ze szczęściem” można również zastosować do powyższej gry
nieskończonej (i innych)? Zastanówmy się, co by to oznaczało. Jeśli
szczęście jest większe niż prawdopodobieństwo zwycięstwa, to my mamy
strategię wygrywającą, a jeśli mniejsze, to wygrywa przeciwnik. Zatem udałoby
nam się zdefiniować prawdopodobieństwo tego, że losowo wybrany punkt
nie należy do zbioru
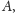 przy użyciu gier. Dla za małych wartości
szczęścia strategię wygrywającą ma przeciwnik, a dla za dużych my. Zatem
możemy zdefiniować prawdopodobieństwo jako najmniejszą wartość
szczęścia, przy której my mamy strategię wygrywającą w danej grze
(a dokładniej kres dolny zbiorów tych wartości).
przy użyciu gier. Dla za małych wartości
szczęścia strategię wygrywającą ma przeciwnik, a dla za dużych my. Zatem
możemy zdefiniować prawdopodobieństwo jako najmniejszą wartość
szczęścia, przy której my mamy strategię wygrywającą w danej grze
(a dokładniej kres dolny zbiorów tych wartości).
Skądinąd wiadomo, że w standardowej matematyce (używającej aksjomatu wyboru) istnieją zbiory niemierzalne, tzn. takie, dla których wartości prawdopodobieństwa nie da się określić. (Jednym z przykładów tego zjawiska może być paradoks Banacha–Tarskiego: można udowodnić, że kulę w przestrzeni trójwymiarowej można podzielić na części, z których można następnie złożyć dwie różne kule, każda takiej samej wielkości jak oryginalna. Gdyby wszystkie zbiory były mierzalne, takiego czegoś nie dałoby się zrobić.)
Czy to oznacza, że konstrukcja gry „ze szczęściem” nie działa dla gier
nieskończonych? Okazuje się, że działa – można udowodnić, że jeśli
strategię wygrywającą mamy my, to miara zewnętrzna (ograniczenie górne
prawdopodobieństwa) dopełnienia
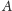 jest mniejsza niż
jest mniejsza niż
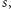 a jeśli
przeciwnik, to miara wewnętrzna (ograniczenie dolne) jest większa. Zauważmy,
że gdyby dla każdej wartości szczęścia któryś z graczy miał strategię
wygrywającą, to zbiór
a jeśli
przeciwnik, to miara wewnętrzna (ograniczenie dolne) jest większa. Zauważmy,
że gdyby dla każdej wartości szczęścia któryś z graczy miał strategię
wygrywającą, to zbiór
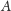 byłby mierzalny (bo miara wewnętrzna jest
większa lub równa wartości granicznej, a zewnętrzna jest mniejsza lub
równa, więc gdy miara zewnętrzna jest mniejsza lub równa od miary
wewnętrznej, to obie muszą być równe). Problem w tym, że istnieją
gry, dla których żaden z graczy nie ma strategii wygrywającej – takie
właśnie gry pojawiają się dla niemierzalnych zbiorów
byłby mierzalny (bo miara wewnętrzna jest
większa lub równa wartości granicznej, a zewnętrzna jest mniejsza lub
równa, więc gdy miara zewnętrzna jest mniejsza lub równa od miary
wewnętrznej, to obie muszą być równe). Problem w tym, że istnieją
gry, dla których żaden z graczy nie ma strategii wygrywającej – takie
właśnie gry pojawiają się dla niemierzalnych zbiorów
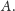 Można
rozważać teorię, w której zamiast aksjomatu wyboru przyjmujemy aksjomat,
że w każdej grze jeden z graczy ma strategię wygrywającą. Wtedy
wszystkie zbiory są mierzalne i rzeczy takie jak paradoks Banacha–Tarskiego
nie mogą mieć miejsca.
Można
rozważać teorię, w której zamiast aksjomatu wyboru przyjmujemy aksjomat,
że w każdej grze jeden z graczy ma strategię wygrywającą. Wtedy
wszystkie zbiory są mierzalne i rzeczy takie jak paradoks Banacha–Tarskiego
nie mogą mieć miejsca.