Rekordy długowieczności i procesy Poissona
Część I: Jak często umiera najstarszy człowiek na Ziemi?
Oczywiście, na tak postawione pytanie matematyka nie udzieli odpowiedzi.
Zbyt wiele czynników ma na to wpływ. Są wśród nich czynniki trudne do
zmierzenia: w jakich jednostkach wyrazilibyśmy, powiedzmy, swój stan
zdrowia lub łaskę bogów (przecież wybrańcy bogów umierają młodo)?
Można jednak rozważyć bardzo uproszczony model, w którym postawione
na wstępie pytanie nabierze matematycznego sensu. Wyobraźmy sobie świat
sprawiedliwy, w którym każdy człowiek w momencie urodzenia ma
jednakowe prawdopodobieństwo
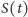 przeżycia ponad
przeżycia ponad
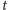 lat.
Nazwiemy
lat.
Nazwiemy
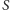 funkcją przeżycia. Z tego, co powiedzieliśmy, wynika, że
funkcją przeżycia. Z tego, co powiedzieliśmy, wynika, że
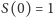 i
i
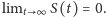 Nie przesądzajmy, czy maksymalny
możliwy czas życia jest skończony, czyli czy istnieje takie
Nie przesądzajmy, czy maksymalny
możliwy czas życia jest skończony, czyli czy istnieje takie
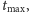 że
że
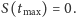 To się okaże nieistotne w naszych rozważaniach.
Nasze wyjściowe założenia możemy sformułować w następujący
sposób:
To się okaże nieistotne w naszych rozważaniach.
Nasze wyjściowe założenia możemy sformułować w następujący
sposób:
- T1
- Każdy noworodek ma jednakową funkcję przeżycia
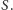
- T2
- Długości życia różnych noworodków są statystycznie niezależne.
Co znaczy założenie T2? Jeśli rozważymy dwóch osobników, to
prawdopodobieństwo tego, że pierwszy przeżyje ponad
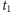 lat i drugi
lat i drugi
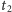 lat, jest równe
lat, jest równe
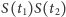 dla dowolnej pary liczb nieujemnych
dla dowolnej pary liczb nieujemnych
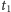 i
i
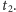 Podobnie prawdopodobieństwa się „przemnażają” dla
trzech i więcej osobników.
Podobnie prawdopodobieństwa się „przemnażają” dla
trzech i więcej osobników.
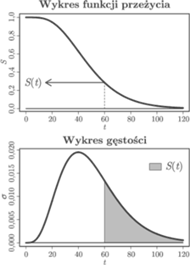
Rys. 1 Całka oznacza pole obszaru pod wykresem funkcji
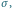 zaznaczonego na dolnej
części rysunku. Górna część rysunku jest wykresem funkcji
zaznaczonego na dolnej
części rysunku. Górna część rysunku jest wykresem funkcji
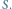
Potrzebny nam będzie jeszcze opis funkcji przeżycia
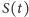 za pomocą tak
zwanej gęstości prawdopodobieństwa. Zdarzenie polegające na tym, że
długość życia pojedynczego osobnika należy do „krótkiego odcinka czasu”
za pomocą tak
zwanej gęstości prawdopodobieństwa. Zdarzenie polegające na tym, że
długość życia pojedynczego osobnika należy do „krótkiego odcinka czasu”
 ma prawdopodobieństwo
ma prawdopodobieństwo
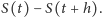 Niech
Niech

Nieformalnie znaczy to, że
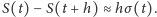 Żeby wyrazić
funkcję
Żeby wyrazić
funkcję
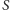 poprzez funkcję
poprzez funkcję
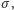 podzielmy przedział
podzielmy przedział
 na
krótkie odcinki długości
na
krótkie odcinki długości
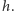 Mamy
Mamy

Przechodząc do granicy z
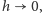 otrzymamy dokładną równość
(patrz rysunek 1).
otrzymamy dokładną równość
(patrz rysunek 1).
Druga grupa założeń mówi z grubsza tyle, że dzieci przychodzą na świat całkowicie losowo i z jednakową intensywnością. W języku rachunku prawdopodobieństwa „strumień narodzin” stanowi jednorodny proces Poissona. Ten niezwykle ciekawy obiekt matematyczny opiszemy poprzez następujące założenia:
- N1
- Dla
dowolnego momentu
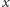 prawdopodobieństwo urodzenia
się dziecka w „krótkim” odcinku czasu
prawdopodobieństwo urodzenia
się dziecka w „krótkim” odcinku czasu
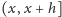 jest
w przybliżeniu równe
jest
w przybliżeniu równe
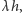 prawdopodobieństwo
zaś urodzenia się więcej niż jednego dziecka jest tak małe,
że możemy je zaniedbać.
prawdopodobieństwo
zaś urodzenia się więcej niż jednego dziecka jest tak małe,
że możemy je zaniedbać.
- N2
- Liczby noworodków pojawiających się w rozłącznych odcinkach czasu są statystycznie niezależne.
Zwróćmy uwagę, że mówimy teraz o „czasie kalendarzowym”, liczonym od
pewnego umownego momentu
 Wyjaśnimy te założenia nieco
dokładniej. Niech
Wyjaśnimy te założenia nieco
dokładniej. Niech
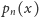 oznacza prawdopodobieństwo tego, że
w przedziale czasowym długości
oznacza prawdopodobieństwo tego, że
w przedziale czasowym długości
 urodzi się dokładnie
urodzi się dokładnie
 dzieci.
Założenie N1 mówi, że
dzieci.
Założenie N1 mówi, że

Oczywiście, z tego wynika, że
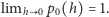 Ukryte w warunku
N1 jest założenie, że liczba narodzin w określonym odcinku czasu zależy
tylko od długości tego odcinka. W naszym szybko zmieniającym się
rzeczywistym świecie oczywiście tak nie jest, ale rozważamy uproszczony
model stacjonarny.
Ukryte w warunku
N1 jest założenie, że liczba narodzin w określonym odcinku czasu zależy
tylko od długości tego odcinka. W naszym szybko zmieniającym się
rzeczywistym świecie oczywiście tak nie jest, ale rozważamy uproszczony
model stacjonarny.
Zacznijmy od wyprowadzenia wzoru wyrażającego
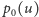 dla dowolnego
dla dowolnego
 Podzielmy odcinek
Podzielmy odcinek
 na sumę
na sumę
 krótkich
odcinków
krótkich
odcinków
 o długości
o długości
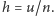 Dla
każdego z tych odcinków prawdopodobieństwo nienarodzenia się dziecka
jest w przybliżeniu równe
Dla
każdego z tych odcinków prawdopodobieństwo nienarodzenia się dziecka
jest w przybliżeniu równe
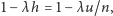 z założenia N1.
Z założenia N2 wynika, że
z założenia N1.
Z założenia N2 wynika, że

Funkcja „exp” w tym wzorze jest to funkcja wykładnicza,
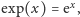 gdzie
podstawa potęgi
gdzie
podstawa potęgi
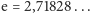 jest tak wybrana, żeby
jest tak wybrana, żeby
 Nieformalnie mówiąc,
Nieformalnie mówiąc,
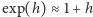 dla
dla
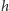 „bliskiego zeru”. Tę własność wykorzystaliśmy w wyprowadzeniu
wzoru na
„bliskiego zeru”. Tę własność wykorzystaliśmy w wyprowadzeniu
wzoru na
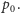 Wykorzystaliśmy także dobrze znaną własność
przysługującą każdej funkcji wykładniczej, mianowicie
Wykorzystaliśmy także dobrze znaną własność
przysługującą każdej funkcji wykładniczej, mianowicie

Stwierdzenie 1.
Prawdopodobieństwo tego, że w odcinku czasu
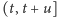 nie urodzi
się ani jedno dziecko, jest dane wzorem:
nie urodzi
się ani jedno dziecko, jest dane wzorem:

Sam ten wynik nie będzie bezpośrednio używany, ale dalsze rozumowania (w nieco bardziej skomplikowanej sytuacji) będą podobne.
Przyjmijmy jeszcze jedno założenie.
- TN
- Długości życia wszystkich osobników są statystycznie niezależne od procesu narodzin.
Spostrzeżenie, które pozwoli nam na rozwiązanie postawionego zadania, jest niezwykle proste.
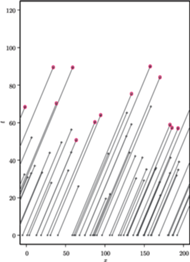
Rys. 2 Symulowany przebieg procesu; kolorowe kółka oznaczają rekordy długowieczności.
Stwierdzenie 2. Zdarzenie polegające na tym, że w „krótkim”
odcinku czasu
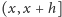 narodzi się osobnik, który przeżyje ponad
narodzi się osobnik, który przeżyje ponad
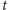 lat, jest w przybliżeniu równe
lat, jest w przybliżeniu równe
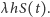
Nasz główny rezultat możemy sformułować w następującej postaci.
Twierdzenie. Prawdopodobieństwo zdarzenia polegającego na tym, że pojedynczy osobnik w momencie śmierci będzie starszy od wszystkich aktualnie żyjących, jest równe

Zanim podamy dowód, zaproponujemy pewną geometryczną interpretację
badanego procesu. Rozważmy układ współrzędnych na płaszczyźnie. Oś
poziomą oznaczymy literką
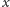 i będziemy na niej zaznaczali czas
„kalendarzowy”. Oś pionowa, oznaczona
i będziemy na niej zaznaczali czas
„kalendarzowy”. Oś pionowa, oznaczona
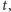 „mierzy” czas życia. Życie
osobnika, który urodził się w momencie
„mierzy” czas życia. Życie
osobnika, który urodził się w momencie
 i przeżył
i przeżył
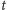 lat,
przedstawimy w postaci odcinka o końcach
lat,
przedstawimy w postaci odcinka o końcach
 i
i
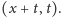
Na rysunku 2 widzimy przykładową realizację opisywanego przez nas procesu.
Punkty na osi
 (czyli momenty narodzin) stanowią, jako się rzekło,
jednorodny proces Poissona. Proces na naszym rysunku ma intensywność
(czyli momenty narodzin) stanowią, jako się rzekło,
jednorodny proces Poissona. Proces na naszym rysunku ma intensywność
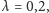 co oznacza, że średnio na jednostkę czasu (powiedzmy, rok)
przypada
co oznacza, że średnio na jednostkę czasu (powiedzmy, rok)
przypada
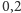 narodzin. Współrzędne pionowe punktów stanowią,
w języku statystyki matematycznej, próbkę z rozkładu prawdopodobieństwa
długości życia, opisanego funkcją
narodzin. Współrzędne pionowe punktów stanowią,
w języku statystyki matematycznej, próbkę z rozkładu prawdopodobieństwa
długości życia, opisanego funkcją
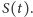 W naszym przykładzie jest to
funkcja przedstawiona na rysunku 1.
W naszym przykładzie jest to
funkcja przedstawiona na rysunku 1.
Sformułujemy następujący wynik pomocniczy.
Lemat 1. Jeśli pewien osobnik umrze w wieku
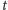 lat, to prawdopodobieństwo tego, że w momencie śmierci będzie
starszy od wszystkich aktualnie żyjących, jest równe
lat, to prawdopodobieństwo tego, że w momencie śmierci będzie
starszy od wszystkich aktualnie żyjących, jest równe

Dowód. Najpierw opiszmy interesujące nas zdarzenie losowe geometrycznie.
Śmierć osobnika, o którym mowa, jest reprezentowana przez punkt
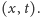 W chwili
W chwili
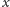 ten osobnik jest najstarszy ze wszystkich
wtedy i tylko wtedy, gdy nie zdarzy się śmierć opisana takim punktem
ten osobnik jest najstarszy ze wszystkich
wtedy i tylko wtedy, gdy nie zdarzy się śmierć opisana takim punktem
 że
że
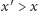 i
i
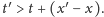 Innymi słowy, mamy
obliczyć prawdopodobieństwo tego, że w obszarze
Innymi słowy, mamy
obliczyć prawdopodobieństwo tego, że w obszarze
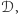 zaznaczonym
na rysunku 3, nie ma „punktów śmierci”.
zaznaczonym
na rysunku 3, nie ma „punktów śmierci”.
Podzielmy obszar
 na „wąskie paski” wysokości
na „wąskie paski” wysokości
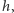 tak jak pokazano
na rysunku 3. Powiemy, że podstawy pasków są to (pionowe) odcinki pomiędzy
punktami
tak jak pokazano
na rysunku 3. Powiemy, że podstawy pasków są to (pionowe) odcinki pomiędzy
punktami
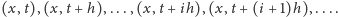 Zajmiemy
się bliżej „typowym paskiem” numer
Zajmiemy
się bliżej „typowym paskiem” numer
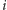 o podstawie
o podstawie
 Zgodnie ze Stwierdzeniem 2 w tym pasku
z prawdopodobieństwem bliskim
Zgodnie ze Stwierdzeniem 2 w tym pasku
z prawdopodobieństwem bliskim
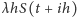 leży jeden „punkt
śmierci”. Prawdopodobieństwo tego, że w tym pasku leżą dwa punkty
lub więcej jest tak małe, że możemy je zaniedbać. Stąd wynika, że
prawdopodobieństwo braku punktów w pasku rozsądnie przybliża
liczba
leży jeden „punkt
śmierci”. Prawdopodobieństwo tego, że w tym pasku leżą dwa punkty
lub więcej jest tak małe, że możemy je zaniedbać. Stąd wynika, że
prawdopodobieństwo braku punktów w pasku rozsądnie przybliża
liczba
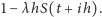 Rzecz jasna, brakuje punktów w całym
obszarze
Rzecz jasna, brakuje punktów w całym
obszarze
 gdy w każdym pasku brak punktów. Z Założeń T2,
N2 i TN wnioskujemy, że obliczane przez nas prawdopodobieństwo
jest iloczynem odpowiednich prawdopodobieństw dla pasków, a więc
w przybliżeniu
gdy w każdym pasku brak punktów. Z Założeń T2,
N2 i TN wnioskujemy, że obliczane przez nas prawdopodobieństwo
jest iloczynem odpowiednich prawdopodobieństw dla pasków, a więc
w przybliżeniu

To jest wyrażenie, które chcieliśmy otrzymać. Wykorzystaliśmy
pewne przybliżone równości, które stają się coraz dokładniejsze,
jeśli
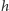 maleje do zera. Przyjmijmy, z przymrużeniem oka, że
„wykazaliśmy słuszność lematu”.
maleje do zera. Przyjmijmy, z przymrużeniem oka, że
„wykazaliśmy słuszność lematu”.
W Lemacie pojawiła się funkcja, którą odtąd będziemy oznaczać

Dowód Twierdzenia. Najtrudniejsze już mamy za sobą. Wystarczy teraz
zsumować prawdopodobieństwa zdarzeń polegających na tym, że
rozpatrywana osoba umarła w przedziale wieku
 i była
w momencie śmierci starsza od wszystkich innych. Korzystając z Lematu,
otrzymujemy
i była
w momencie śmierci starsza od wszystkich innych. Korzystając z Lematu,
otrzymujemy

Przejście do granicy z
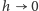 zmienia przybliżenia w dokładne
równości i kończy dowód twierdzenia.
zmienia przybliżenia w dokładne
równości i kończy dowód twierdzenia.
Dygresje i komentarze za miesiąc.
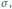 zaznaczonego na dolnej
części rysunku. Górna część rysunku jest wykresem funkcji
zaznaczonego na dolnej
części rysunku. Górna część rysunku jest wykresem funkcji