O polowaniu na pchłę i czekaniu na dwa orły, czyli trochę o łańcuchach Markowa
Zacznijmy od prostego przykładu. Pchła skacze między ziemią, kotem
i człowiekiem. Za każdym razem wybiera miejsce docelowe z takim
samym prawdopodobieństwem (równym
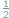 ). Mogłaby tak skakać
w nieskończoność, gdyby nie to, że po wskoczeniu na człowieka ginie. Ile
średnio skoków pchła wykona przed śmiercią, jeżeli zaczyna na
ziemi?
). Mogłaby tak skakać
w nieskończoność, gdyby nie to, że po wskoczeniu na człowieka ginie. Ile
średnio skoków pchła wykona przed śmiercią, jeżeli zaczyna na
ziemi?
Zadanie rozwiążemy bez trudu, pamiętając, że średnia wartość zmiennej losowej to suma wszystkich iloczynów postaci
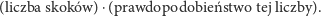 |
Po prostu wypiszemy wszystkie możliwe drogi pchły: zginie ona po 1 skoku, jeżeli
od razu skoczy na człowieka, co zapisujemy
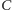 ; po 2 skokach –
; po 2 skokach –
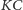 (najpierw na kota, potem na człowieka), po 3 skokach –
(najpierw na kota, potem na człowieka), po 3 skokach –
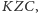 po 4
skokach –
po 4
skokach –
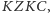 i tak dalej. Każdy taki ciąg długości
i tak dalej. Każdy taki ciąg długości
 ma
prawdopodobieństwo
ma
prawdopodobieństwo
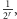
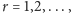 a zatem średnio pchła
wykona
a zatem średnio pchła
wykona
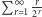 skoków. Oznaczając
skoków. Oznaczając
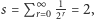 średnią
ilość skoków pchły możemy wyznaczyć, sumując poniższe wyrażenie
kolumnami:
średnią
ilość skoków pchły możemy wyznaczyć, sumując poniższe wyrażenie
kolumnami:

A zatem pchła wykona średnio 2 skoki.
Rozbudujmy ten przykład i wpuśćmy do pokoju psa. Zasady skoków pchły
pozostają takie same, ale teraz prawdopodobieństwo wyboru każdego
docelowego miejsca skoku to
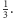 Możemy rozwiązywać zadanie tak
samo jak przedtem – będzie to nieco dłuższe, ale nadal wykonalne.
Możemy rozwiązywać zadanie tak
samo jak przedtem – będzie to nieco dłuższe, ale nadal wykonalne.
Można też nieco inaczej. W obu powyższych zagadnieniach miejsce
kolejnego przeskoku zależy tylko od tego, gdzie pchła znajduje się w danej
chwili, a nie od jej przeszłej podróży. Ponadto z góry wiadomo, jakie
są możliwe położenia pchły, tak zwane stany –
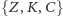 lub
lub
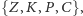 oraz jakie są reguły poruszania się między stanami. Oznacza
to, że w obu przypadkach mamy do czynienia z łańcuchem Markowa.
Reguły przeskoku to prawdopodobieństwa przejścia między stanami.
Prawdopodobieństwo przejścia ze stanu
oraz jakie są reguły poruszania się między stanami. Oznacza
to, że w obu przypadkach mamy do czynienia z łańcuchem Markowa.
Reguły przeskoku to prawdopodobieństwa przejścia między stanami.
Prawdopodobieństwo przejścia ze stanu
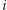 do stanu
do stanu
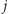 oznaczamy
przez
oznaczamy
przez
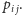
W zagadnieniu I mamy:
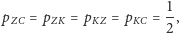 |
dla kompletności przyjmiemy jeszcze
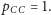 W zagadnieniu II jest
podobnie:
W zagadnieniu II jest
podobnie:

oraz
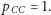 Wygodnie jest zapisać takie prawdopodobieństwa
w macierzy albo wyrysować je jako graf. Na przykład dla właściciela dwóch
zwierząt macierz oraz graf będą wyglądać następująco:
Wygodnie jest zapisać takie prawdopodobieństwa
w macierzy albo wyrysować je jako graf. Na przykład dla właściciela dwóch
zwierząt macierz oraz graf będą wyglądać następująco:
 |
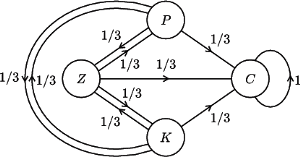
W ogólnej sytuacji powiemy, że ciąg zmiennych losowych
 tworzy jednorodny łańcuch Markowa o przestrzeni stanów
tworzy jednorodny łańcuch Markowa o przestrzeni stanów
 jeżeli dla dowolnego
jeżeli dla dowolnego
 i dowolnego
ciągu stanów
i dowolnego
ciągu stanów
 mamy
mamy
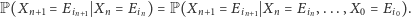 |
Oznacza to, że dochodząc do każdego stanu, łańcuch „zapomina”, skąd przyszedł, a prawdopodobieństwa przejścia w następnym ruchu zależą tylko od położenia bieżącego. Własność tę nazywamy własnością Markowa i tak właśnie jest w powyższych przykładach.
Teraz rozwiążemy zadanie o średnim czasie życia pchły dla łańcucha
Markowa o grafie jak wyżej. Niech
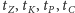 oznaczają średnie
czasy życia pchły startującej odpowiednio z ziemi, kota, psa, człowieka.
Oczywiście, mamy
oznaczają średnie
czasy życia pchły startującej odpowiednio z ziemi, kota, psa, człowieka.
Oczywiście, mamy
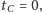 a pozostałe czasy życia możemy
związać układem równań, wykorzystując wzór na prawdopodobieństwo
całkowite i własność Markowa. Na przykład, jeżeli startujemy z ziemi,
to po wykonaniu jednego skoku przechodzimy do jednego ze stanów
a pozostałe czasy życia możemy
związać układem równań, wykorzystując wzór na prawdopodobieństwo
całkowite i własność Markowa. Na przykład, jeżeli startujemy z ziemi,
to po wykonaniu jednego skoku przechodzimy do jednego ze stanów
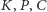 z prawdopodobieństwem
z prawdopodobieństwem
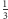 i kontynuujemy skoki z tych
nowych stanów, zapominając o przeszłości, ale za to zwiększając „odczyt
licznika” o
i kontynuujemy skoki z tych
nowych stanów, zapominając o przeszłości, ale za to zwiększając „odczyt
licznika” o
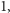 bo jeden skok już wykonaliśmy. Otrzymujemy układ
równań:
bo jeden skok już wykonaliśmy. Otrzymujemy układ
równań:

Rozwiązując go, natychmiast dostaniemy, że
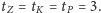
A jeśli człowiek ma gorszy refleks i szansa na to, że zabije pchłę, która
na niego wskoczyła, wynosi
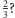 Jeżeli pchła przeżyje kontakt
z człowiekiem, to przerażona (czy pchła się boi?) nie zastanawia się już, co ma
zrobić (czy pchła się zastanawia?) i zeskakuje na ziemię. Dla opisania ruchu
pchły dodamy osobny stan
Jeżeli pchła przeżyje kontakt
z człowiekiem, to przerażona (czy pchła się boi?) nie zastanawia się już, co ma
zrobić (czy pchła się zastanawia?) i zeskakuje na ziemię. Dla opisania ruchu
pchły dodamy osobny stan
 (po angielsku nazywany cemetery state), do
którego można dojść tylko z
(po angielsku nazywany cemetery state), do
którego można dojść tylko z
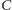 i z którego nie można już
wyjść. Graf będzie teraz taki.
i z którego nie można już
wyjść. Graf będzie teraz taki.
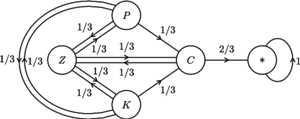
Uważny Czytelnik zauważy, że powyższy graf nie do końca odpowiada omawianej sytuacji. Graf ten uwzględnia dodatkowy krok między wskoczeniem na człowieka a śmiercią pchły, którego w rzeczywistości nie dodaje się do czasu jej życia.
Postępując jak wcześniej, wypiszemy układ równań na czasy dojścia do
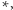 odpowiadający grafowi 2:
odpowiadający grafowi 2:

Zwróćmy uwagę, że teraz zamiast
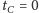 będziemy mieli
będziemy mieli
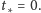 Rozwiązując ten układ, dostaniemy
Rozwiązując ten układ, dostaniemy
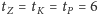 ;
;
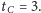 Liczba
Liczba
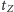 nie jest jednak średnim czasem życia pchły –
czas życia będzie o
nie jest jednak średnim czasem życia pchły –
czas życia będzie o
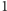 mniejszy, bo przecież dodaliśmy jeden krok na
przejście
mniejszy, bo przecież dodaliśmy jeden krok na
przejście
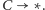 Zatem pchła średnio wykona 5 skoków, zanim
zginie.
Zatem pchła średnio wykona 5 skoków, zanim
zginie.
Rozważymy teraz pozornie zupełnie inne zagadnienie. Adaś i Bolek
obserwują wyniki kolejnych rzutów niesymetryczną monetą, dla której
prawdopodobieństwo wyrzucenia orła to
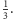 Założyli się o czekoladę:
Adaś wygra, jeżeli dwa orły pod rząd wypadną, zanim Bolek doczeka się serii
trzech reszek, a Bolek – jeśli to trzy reszki pojawią się wcześniej. Jakie jest
prawdopodobieństwo tego, że wygra Adaś?
Założyli się o czekoladę:
Adaś wygra, jeżeli dwa orły pod rząd wypadną, zanim Bolek doczeka się serii
trzech reszek, a Bolek – jeśli to trzy reszki pojawią się wcześniej. Jakie jest
prawdopodobieństwo tego, że wygra Adaś?
Czy wiesz, Czytelniku, czemu ta gra z prawdopodobieństwem 1 zakończy się po skończonej liczbie rzutów?
Zastanówmy się, gdzie można w tym zagadnieniu dopatrzeć się łańcucha
Markowa. Otóż będziemy rozważali tylko takie końcówki ciągów,
które mogą być kontynuowane jako rozstrzygające grę
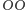 albo
albo
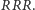
Na przykład, jeżeli wykonano 5 rzutów, w których po kolei wypadło
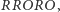 to układ będzie w stanie
to układ będzie w stanie
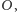 bo
bo
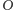 jest
początkiem pożądanego ciągu
jest
początkiem pożądanego ciągu
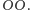 Gdyby natomiast wynikiem
było
Gdyby natomiast wynikiem
było
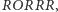 to układ byłby w stanie
to układ byłby w stanie
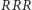 – byłaby to
wygrana Bolka i koniec zabawy. Możliwe stany układu są więc następujące:
– byłaby to
wygrana Bolka i koniec zabawy. Możliwe stany układu są więc następujące:
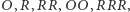 a prawdopodobieństwa przejścia to
a prawdopodobieństwa przejścia to

Musimy jeszcze dopowiedzieć, że po pierwszym rzucie z prawdopodobieństwem
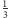 wchodzimy w stan
wchodzimy w stan
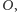 a z prawdopodobieństwem
a z prawdopodobieństwem
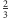 –
w stan
–
w stan
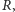 i to określa pierwszy krok. Adaś wygra, jeżeli uda się
dojść do stanu
i to określa pierwszy krok. Adaś wygra, jeżeli uda się
dojść do stanu
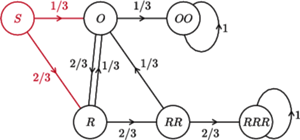
 Graf układu wygląda następująco.
Graf układu wygląda następująco.
Analogicznie jak w zadaniu o średnim czasie życia pchły, możemy ułożyć
układ równań, w którym powiążemy prawdopodobieństwa wygranej Adasia
przy starcie ze stanów
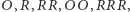 oznaczone odpowiednio przez
oznaczone odpowiednio przez
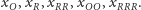 Wykonujemy krok w przód, patrzymy, gdzie
dotarliśmy, korzystamy ze wzoru na prawdopodobieństwo całkowite, a następnie
z własności Markowa (tj. zapominamy, skąd przyszliśmy), i rozważamy
prawdopodobieństwa wygranej Adasia przy starcie z nowych położeń. Na
przykład, ze stanu
Wykonujemy krok w przód, patrzymy, gdzie
dotarliśmy, korzystamy ze wzoru na prawdopodobieństwo całkowite, a następnie
z własności Markowa (tj. zapominamy, skąd przyszliśmy), i rozważamy
prawdopodobieństwa wygranej Adasia przy starcie z nowych położeń. Na
przykład, ze stanu
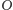 przechodzimy z prawdopodobieństwem
przechodzimy z prawdopodobieństwem
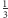 do stanu
do stanu
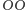 i z prawdopodobieństwem
i z prawdopodobieństwem
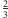 do stanu
do stanu
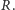 Otrzymujemy układ równań:
Otrzymujemy układ równań:

przy czym mamy
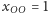 i
i
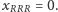 Rozwiązaniem układu są
liczby:
Rozwiązaniem układu są
liczby:
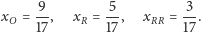 |
Ponieważ po pierwszym kroku znajdziemy się w stanie
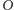 lub
lub
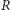 (z prawdopodobieństwem odpowiednio
(z prawdopodobieństwem odpowiednio
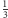 i
i
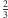 ), to
prawdopodobieństwo wygranej Adasia wynosi
), to
prawdopodobieństwo wygranej Adasia wynosi
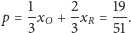 |
Może Adaś nie lubi czekolady?
Pozostawiamy Czytelnikowi do samodzielnego rozwiązania zadanie: jeżeli moneta jest symetryczna, to jaki będzie średni czas trwania gry? (Odpowiedź)
O tym, co się dzieje z łańcuchami Markowa po długim czasie, dowiesz się Czytelniku z drugiej części artykułu (Delta 12/2013).
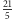 ruchu.
ruchu.