Gramy na kumulację. Kilka uwag o grze w Lotto.
Organizatorzy gier liczbowych typu lotto przeznaczają sporą część dochodu na zysk i koszt pozyskania dochodu i ten fakt sprawia, że wiele osób powstrzymuje się od gry, a dopiero mechanizm kumulacji powoduje zainteresowanie grą. Dla organizatorów gier kumulacja jest tylko formą odłożenia wypłaty, przeto nic na niej nie tracą, natomiast nowi grający, oczekujący zysku z podziału kwoty odłożonej, grają przeciw stałym graczom.

Gra
Przyjmijmy, że w grze uczestniczy
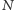 osób, a stawka wynosi 1 złoty.
Dochód
osób, a stawka wynosi 1 złoty.
Dochód
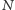 dzieli się na części:
dzieli się na części:
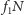 – część wzięta
przez organizatora,
– część wzięta
przez organizatora,
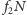 – pula wygranych I stopnia (szóstek),
– pula wygranych I stopnia (szóstek),
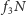 – pula wygranych niższego stopnia. Gdy w danej grze szóstka
nie padnie, ta druga część przenosi się na kolejną grę i mamy pierwszą
kumulację. Brak szóstki w kolejnych grach daje sensacyjne niekiedy serie
kumulacji. Pojawienie się szóstki w grze przerywa ciąg kumulacji, jest chwilą
swoistej odnowy w ciągu gier.
– pula wygranych niższego stopnia. Gdy w danej grze szóstka
nie padnie, ta druga część przenosi się na kolejną grę i mamy pierwszą
kumulację. Brak szóstki w kolejnych grach daje sensacyjne niekiedy serie
kumulacji. Pojawienie się szóstki w grze przerywa ciąg kumulacji, jest chwilą
swoistej odnowy w ciągu gier.
W Lotto mamy dwa mechanizmy losowe: wybór szóstki
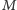 przez
maszynę i wybór szóstki
przez
maszynę i wybór szóstki
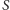 przez gracza. Można założyć, że oba te
losowania są niezależne. Rozkład
przez gracza. Można założyć, że oba te
losowania są niezależne. Rozkład
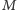 jest jednostajny:
jest jednostajny:

na zbiorze wszystkich możliwych szóstek
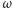 wybranych spośród
49 liczb, natomiast
wybranych spośród
49 liczb, natomiast
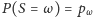 zależy od upodobań graczy.
Ten drugi rozkład może być poznawany jedynie przez statystyków.
Prawdopodobieństwo koincydencji wynosi
zależy od upodobań graczy.
Ten drugi rozkład może być poznawany jedynie przez statystyków.
Prawdopodobieństwo koincydencji wynosi

Liczba szóstek
Niech
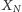 oznacza liczbę szóstek w grze przy udziale
oznacza liczbę szóstek w grze przy udziale
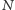 osób.
Jeśli założyć, że grający losują liczby wzajemnie niezależnie i mają
określone predylekcje do liczb, ale nie mają ich do układów, to
osób.
Jeśli założyć, że grający losują liczby wzajemnie niezależnie i mają
określone predylekcje do liczb, ale nie mają ich do układów, to

Prawdopodobieństwo powstania kumulacji wynosi
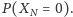 Oczekiwana
liczba szóstek w grze jest stała,
Oczekiwana
liczba szóstek w grze jest stała,
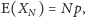 natomiast predylekcje
zwiększają wariancję liczby głównych wygranych. Prosty rachunek daje
wariancję
natomiast predylekcje
zwiększają wariancję liczby głównych wygranych. Prosty rachunek daje
wariancję

Ten fakt wyjaśnia, dlaczego w praktyce liczba wygranych I stopnia jest tak bardzo zmienna.

Gra na kumulację
Oznaczmy przez
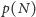 prawdopodobieństwo pojawienia się przynajmniej
jednej szóstki wśród
prawdopodobieństwo pojawienia się przynajmniej
jednej szóstki wśród
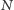 kuponów. Jest ono dość chimeryczne,
zależy od liczb wylosowanych przez maszynę losującą i od upodobań grających
do określonych liczb i ich konfiguracji. Gdyby gracze wybierali swoje typy jak
maszyna, to mielibyśmy
kuponów. Jest ono dość chimeryczne,
zależy od liczb wylosowanych przez maszynę losującą i od upodobań grających
do określonych liczb i ich konfiguracji. Gdyby gracze wybierali swoje typy jak
maszyna, to mielibyśmy

Odnotujmy, że
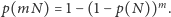 Przyjmijmy, że skumulowane
kwoty na nagrody I stopnia wynoszą
Przyjmijmy, że skumulowane
kwoty na nagrody I stopnia wynoszą
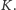 Oczekiwaną wygraną
Oczekiwaną wygraną
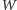 przypadającą na jeden kupon można znaleźć, dzieląc pulę nagród
przez liczbę grających. Mamy
przypadającą na jeden kupon można znaleźć, dzieląc pulę nagród
przez liczbę grających. Mamy

Wiadomo, że kumulacja powoduje wzrost liczby grających, a rzesza
konkurentów do podziału kwoty odłożonej zmniejsza nasze szanse na sukces.
Przy rosnącej liczbie grających prawdopodobieństwo kumulacji znika,
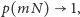 gdy
gdy
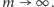 Aby wejść do gry, należy trafnie
przewidzieć liczbę grających. Statystyczną pewność (rozumianą jako
zdarzenie o prawdopodobieństwie 0,95) tego, że wygrana I stopnia padnie,
mamy dopiero przy
Aby wejść do gry, należy trafnie
przewidzieć liczbę grających. Statystyczną pewność (rozumianą jako
zdarzenie o prawdopodobieństwie 0,95) tego, że wygrana I stopnia padnie,
mamy dopiero przy
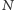 przekraczającym 42 miliony kuponów. Przy
dużym
przekraczającym 42 miliony kuponów. Przy
dużym
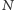 warunek
warunek
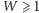 opłacalności gry implikuje
opłacalności gry implikuje
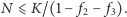
Wzrost liczby grających
Ocena wzrostu liczby grających w zależności od wielkości kumulacji jest
trudnym problemem dla analityków gier. Przyjmijmy, że wzrost ten w ciągu
kumulacji jest potęgowy: liczba grających w
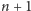 kolejnych grach będzie
równa
kolejnych grach będzie
równa
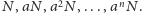 Pula nagród I stopnia przy
Pula nagród I stopnia przy
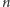 -tej
kumulacji wynosi
-tej
kumulacji wynosi

Oczekiwana wygrana w
 -tej kumulacji wynosi więc
-tej kumulacji wynosi więc

Przypuśćmy teraz, że liczba grających jest proporcjonalna do kumulacji.
Niech
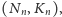
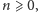 oznaczają liczbę grających i kwotę
kumulacji w serii. Ściśle biorąc, jeśli przyrost liczby grających jest
proporcjonalny (ze współczynnikiem proporcjonalności
oznaczają liczbę grających i kwotę
kumulacji w serii. Ściśle biorąc, jeśli przyrost liczby grających jest
proporcjonalny (ze współczynnikiem proporcjonalności
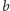 ) do
funduszu szóstek, to zachodzą wzory rekurencyjne:
) do
funduszu szóstek, to zachodzą wzory rekurencyjne:

Zwrot w
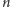 -tej grze wynosi
-tej grze wynosi

Obliczenia
Przeanalizujmy czas czekania na korzystne wejście do gry. Obserwując
częstość pojawienia się pierwszej kumulacji, wielkość
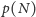 można
próbować oszacować. Niepoprawny optymista, nie mając danych, może
przyjąć, że jest ono równe 1.
można
próbować oszacować. Niepoprawny optymista, nie mając danych, może
przyjąć, że jest ono równe 1.
Weźmy dla przykładu
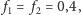
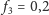 i niech
i niech
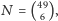 a wtedy
a wtedy
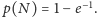 Eksperymenty numeryczne
pokażą, jak wzrost liczebności grających wpływa na czas wejścia do gry.
Przy wzroście potęgowym szukamy chwili, kiedy po raz pierwszy jest
Eksperymenty numeryczne
pokażą, jak wzrost liczebności grających wpływa na czas wejścia do gry.
Przy wzroście potęgowym szukamy chwili, kiedy po raz pierwszy jest
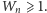 Obliczenia pokazują, że przy
Obliczenia pokazują, że przy
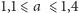 mamy
mamy
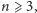 przy czym dla
przy czym dla
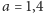 mamy
mamy
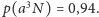 Przy
wzroście proporcjonalnym szansa na zwrot
Przy
wzroście proporcjonalnym szansa na zwrot
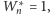 gdy
gdy
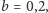 pojawia się przy sześciu kumulacjach. Przy
pojawia się przy sześciu kumulacjach. Przy
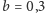 liczba
grających rośnie tak szybko, że w grze na kumulację nie ma miejsca
na zysk.
liczba
grających rośnie tak szybko, że w grze na kumulację nie ma miejsca
na zysk.

Manipulacja
Organizator gry, zainteresowany wzrostem liczby grających, może modyfikować
podział puli na nagrody tak, ażeby kwota skumulowana rosła szybko, ma więc
narzędzie do manipulowania klientami. Eksperymentując wielkością puli
nagród poszczególnych stopni, pozostawmy zysk organizatora bez zmiany,
przeznaczmy
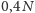 na wygrane niższego stopnia i
na wygrane niższego stopnia i
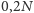 na
wygrane I stopnia. Zmiana nie wpłynie na liczbę wygranych, natomiast podwoi
wygrane niższych stopni i zmniejszy kwoty skumulowane. Teraz czas czekania
na korzystną kumulację wydłuży się. Przy wzroście potęgowym i
na
wygrane I stopnia. Zmiana nie wpłynie na liczbę wygranych, natomiast podwoi
wygrane niższych stopni i zmniejszy kwoty skumulowane. Teraz czas czekania
na korzystną kumulację wydłuży się. Przy wzroście potęgowym i
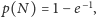 dla
dla
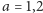 otrzymujemy
otrzymujemy
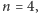 przy
przy
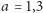 otrzymamy
otrzymamy
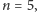 itd. Trzeba jednak pamiętać, że kiedy
liczba grających wzrasta gwałtownie, warunki do gry na kumulację mogą
nie być osiągnięte, nim padnie szóstka. Dodajmy jeszcze, zanim przystąpimy
do gry na kumulację, że gigantyczne wygrane mają małą użyteczność dla
szczęśliwców. Ale jest to już inny problem.
itd. Trzeba jednak pamiętać, że kiedy
liczba grających wzrasta gwałtownie, warunki do gry na kumulację mogą
nie być osiągnięte, nim padnie szóstka. Dodajmy jeszcze, zanim przystąpimy
do gry na kumulację, że gigantyczne wygrane mają małą użyteczność dla
szczęśliwców. Ale jest to już inny problem.
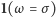 oznacza funkcję, która przyjmuje wartość 1, gdy
oznacza funkcję, która przyjmuje wartość 1, gdy
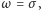 a w pozostałych przypadkach jej wartością jest 0.
a w pozostałych przypadkach jej wartością jest 0.