Nie wiemy, jak zachowaliby się gracze, grający w taką grę. Czy dałoby się zauważyć podział na grupy, odpowiadające kilku charakterystycznym strategiom? Dzięki autorom pracy [1] wiemy natomiast, jak zachowują się ludzie, postawieni przed znacznie bardziej skomplikowanym dynamicznym problemem decyzyjnym, gdzie ze względu na złożoność obliczeniową nikt nie jest w stanie w trakcie gry znaleźć strategii optymalnej.

Oto opis eksperymentu. Gra składa się z 15 rund. W każdej rundzie należy wybrać wypłatę, odpowiadającą jednej z opcji: 1 lub 2. Gracz widzi przed podjęciem decyzji proponowane wypłaty. Ostateczna wygrana jest sumą wypłat z 15 rund.

Jednak przyszłe wypłaty z opcji 1 zależą od historii gry, podczas gdy wypłaty z opcji 2 – nie. Ponadto wszystkie wypłaty są nieujemne.

A dokładniej:

Dla opcji 1:

• wypłata zasadnicza ;
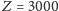• premia 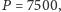 gdy poprzednio wybraliśmy opcję 1 od 6 do 9 razy, i równa zeru w przeciwnym razie;
• koszt 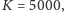 gdy poprzednio wybraliśmy opcję 2, w przeciwnym razie zero;
• loteria: 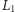 jest zmienną losową o rozkładzie jednostajnym na przedziale
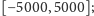
• łączna wypłata

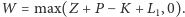
Dla opcji 2:

• wypłata zasadnicza
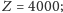
• loteria: 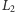 jest zmienną losową o rozkładzie jednostajnym na przedziale
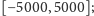
• łączna wypłata

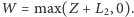
Przy generowaniu wypłat dla opcji 1 i 2 zmienne losowe 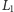 i 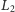 są niezależne. Są także niezależne od loterii z poprzednich rund.

Uczestnicy eksperymentu mieli możliwość krótkiego treningu przed właściwym testem.

Co się okazało? Autorzy pracy [1] twierdzą, że analiza wzorców zachowania graczy pozwala podzielić ich na trzy grupy, nazwane dość rozsądni (near-rational), fataliści (fatalists) i zagubieni (confused). Gracze z pierwszej grupy (37% całości) tracili średnio zaledwie 2,3% w porównaniu ze strategią optymalną, podczas gdy fataliści (było ich 40%) – 11,7%, wreszcie zagubieni (24%) – 18,6%.

Skąd takie nazwy grup? W bardzo dużym skrócie przedstawiamy argumentację autorów. Gracze „dość rozsądni” zrozumieli, że należy dążyć do uzyskania premii w 6, 7, 8 i 9 rundzie, wobec tego opcję 2 warto wybierać tylko wtedy, gdy ma dużą przewagę. Mało tego, potrafili z niezłą dokładnością oszacować, jaka musi być ta przewaga – a zależy ona od historii gry. Fataliści nie wiedzą, jaki jest charakter tej zależności, choć zdają sobie z grubsza sprawę, jak należy grać, i dlatego w efekcie zdają się na los szczęścia. Zagubieni tracą głowę w rundzie 5 i następnych: przeceniają opcję 2, i w efekcie – wbrew oczekiwaniom – nie uzyskują premii. Ponadto wariancja wygranej jest w tej grupie większa niż w pozostałych.

Wygląda na to, że ludzie postawieni przed trudnym problemem wykazują niewiele fantazji i wybierają spośród niewielu rozwiązań.

Ciekawe, jakie byłyby typowe reakcje na następujący