Omega
Wół, lis i konik polny
Czarownica
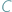 w punkcie
w punkcie
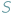 na rozstaju dróg mówi do lisa
na rozstaju dróg mówi do lisa
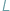 , wołu
, wołu
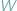 i konika polnego
i konika polnego
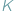 : „Pójdziesz w prawo,
dostaniesz pół złotego, ...
: „Pójdziesz w prawo,
dostaniesz pół złotego, ...
... pójdziesz w lewo, dostaniesz garść miedziaków z sakiewki – możesz je
sobie przeliczyć. Ja jestem uczciwą czarownicą i kwota wyciągnięta z sakiewki
ma rozkład prawie jednostajny na przedziale
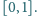
Średnio dostajesz pół złotego. Chodziłeś do szkół – będziesz wiedział, co to znaczy. Nie chce mi się więcej gadać, rzuć okiem na plan. Uważaj na wiedźmina z dwójki. Pójdziesz w lewo – on weźmie z garści miedziaków coś na piwo (ile się da, ale nie więcej niż ćwierć złotego) i wypłaci resztę – jeśli zostanie”.
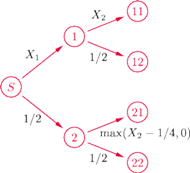
Może i słusznie czarownicy nie chciało się gadać. Formalny opis
gry jest prosty. Wymaga dwóch niezależnych zmiennych losowych
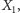
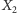 o rozkładzie jednostajnym na przedziale
o rozkładzie jednostajnym na przedziale
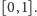 Oto
wypłaty odpowiadające czterem możliwym drogom:
Oto
wypłaty odpowiadające czterem możliwym drogom:

W trzech przypadkach średnia wypłata jest równa 1, w jednym – nieco mniejsza.
Na rozstaju pojawia się wół, który nie lubi niespodzianek. Idzie dwa razy w prawo, wygrywa średnio (i zawsze) złotówkę. Konik polny lubi ryzyko, ale nie myśli. Idzie dwa razy w lewo, średnio dostaje złotówkę.
Lis akceptuje ryzyko i myśli. A myśli tak: jeśli za pierwszym razem
miedziaków będzie mało, pójdę w prawo. I tak mam gwarantowane pół złotego,
a może będzie lepiej? Ostatecznie lis (po konsultacji z niedźwiedziem)
dochodzi do ogólnej teorii. Najpierw rozważa wypłaty w ostatnim kroku, gdzie
wybór drogi jest oczywisty: niezależnie od tego, co już ma, wybiera większą z
oferowanych wypłat. W stanie 1 otrzyma zatem
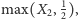 a w stanie 2
–
a w stanie 2
–
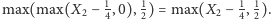 Może nawet obliczyć
średnie (szybki sposób na końcu artykułu):
Może nawet obliczyć
średnie (szybki sposób na końcu artykułu):

To z kolei umożliwi mu podjęcie decyzji na starcie. Jeśli

czyli
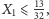 to idzie w prawo (teraz już wie dokładnie, co to znaczy, że
miedziaków jest za mało: progiem decyzyjnym jest
to idzie w prawo (teraz już wie dokładnie, co to znaczy, że
miedziaków jest za mało: progiem decyzyjnym jest
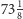 kwartnika).
W przeciwnym razie idzie w lewo. Co na tym zyskuje?
kwartnika).
W przeciwnym razie idzie w lewo. Co na tym zyskuje?
Zobaczmy. Średnia wygrana w pierwszym kroku jest równa

gdzie pierwszy składnik odpowiada drodze w lewo, drugi – w prawo. Symbol
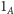 oznacza zmienną losową wskaźnikową zdarzenia
oznacza zmienną losową wskaźnikową zdarzenia
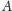 : przyjmuje
ona wartość 1 na
: przyjmuje
ona wartość 1 na
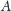 i 0 na
i 0 na
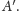 W efekcie
W efekcie
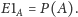
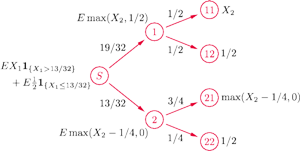
Drogę w lewo wybieramy z prawdopodobieństwem
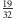 i wygrywamy
w drugim kroku średnio
i wygrywamy
w drugim kroku średnio
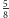 ; dla drogi w prawo odpowiednie
wielkości są równe
; dla drogi w prawo odpowiednie
wielkości są równe
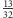 i
i
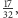 zatem średnio w drugim kroku
mamy
zatem średnio w drugim kroku
mamy

Ostatecznie lis wygrywa średnio

czyli o ponad 20% więcej niż wół i konik polny. W istocie lis znalazł sposób na uzyskanie największej możliwej średniej wygranej (czego nie udowodnimy).
Wyjaśnimy natomiast na zakończenie, jak zostały obliczone występujące
powyżej średnie. Jeśli
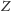 jest nieujemną zmienną losową, to
jest nieujemną zmienną losową, to

Gdy
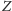 ma rozkład ciągły, wzór ten można otrzymać rutynowo:
całkując przez części. Ale najbardziej pożyteczny staje się on w przypadku
bardziej ogólnych rozkładów.
ma rozkład ciągły, wzór ten można otrzymać rutynowo:
całkując przez części. Ale najbardziej pożyteczny staje się on w przypadku
bardziej ogólnych rozkładów.
Obliczenie
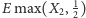 sprowadza się do obliczenia pola prostej figury
geometrycznej. Z kolei
sprowadza się do obliczenia pola prostej figury
geometrycznej. Z kolei
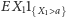 jest polem trapezu o wysokości
jest polem trapezu o wysokości
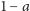 i bokach
i bokach
 oraz 1; prosimy Czytelnika o sprawdzenie.
oraz 1; prosimy Czytelnika o sprawdzenie.