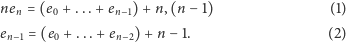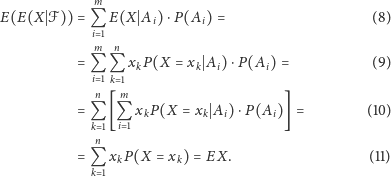Złośliwe świnki
W dziale naukowym jednej z gazet pojawiło się następujące zadanie...
Zadanie. Jest sto skarbonek (to tytułowe świnki) z kluczykami. Każdy kluczyk pasuje tylko do jednej skarbonki. Skarbonki zamykamy, a wymieszane losowo kluczyki wrzucamy po jednym do każdej skarbonki. Teraz tłuczemy jedną skarbonkę, a wyjętym z niej kluczykiem otwieramy następną, etc. Jaka jest szansa, że pozostałe skarbonki uda się otworzyć bez rozbijania?
Do wyboru były cztery odpowiedzi: a)
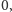 b)
b)
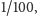 c)
c)
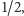 d)
d)
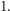 Wielu czytelników uważało jednak, że żadna z podanych
odpowiedzi nie jest prawdziwa, na ogół z powodu skojarzenia z dobrze
znanym zadaniem o kapeluszach: jeśli
Wielu czytelników uważało jednak, że żadna z podanych
odpowiedzi nie jest prawdziwa, na ogół z powodu skojarzenia z dobrze
znanym zadaniem o kapeluszach: jeśli
 osób włoży losowo
osób włoży losowo
 kapeluszy, to z prawdopodobieństwem równym
kapeluszy, to z prawdopodobieństwem równym

żadna z nich nie będzie miała swojego kapelusza na głowie.
Co gorsza, piszący te słowa obserwowali to zjawisko na sobie i swoich
studentach. Pierwszym odruchem była uwaga:
aha, jeśli żaden kluczyk nie
znajdzie się w skarbonce, którą otwiera, to otworzymy po kolei wszystkie.
Owszem, jest to warunek konieczny, ale nie dostateczny. Otóż operacja uda się
wtedy i tylko wtedy, gdy kluczyk od rozbitej skarbonki pojawi się na końcu.
A szansa na to – ze względu na symetrię – jest równa
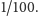 Gdyby
ktoś nie wierzył, może rozwiązać zadanie formalnie. Rozważmy
Gdyby
ktoś nie wierzył, może rozwiązać zadanie formalnie. Rozważmy
 skarbonek. Zdarzeniami elementarnymi, które uznajemy za jednakowo
prawdopodobne, są
skarbonek. Zdarzeniami elementarnymi, które uznajemy za jednakowo
prawdopodobne, są
 -elementowe ciągi kluczyków. Takich ciągów jest
-elementowe ciągi kluczyków. Takich ciągów jest
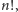 zdarzeniami sprzyjającymi są zaś te, w których kluczyk od rozbitej
skarbonki pojawia się na końcu. Jest ich
zdarzeniami sprzyjającymi są zaś te, w których kluczyk od rozbitej
skarbonki pojawia się na końcu. Jest ich
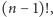 stąd szukane
prawdopodobieństwo wynosi
stąd szukane
prawdopodobieństwo wynosi

Niestety, właściwe rozwiązanie przychodzi zwykle do głowy poniewczasie. Świnki są naprawdę złośliwe. Dlatego będziemy je tłuc bardziej intensywnie.
Załóżmy, że w chwili pojawienia się kluczyka niepasującego do żadnej skarbonki tłuczemy kolejną. Ile średnio trzeba stłuc skarbonek, by otworzyć wszystkie?
Czytelnik może spróbować odgadnąć rząd wielkości. Średnia jest zaskakująco nieduża i wynosi

Dla
 skarbonek średnia, którą oznaczymy przez
skarbonek średnia, którą oznaczymy przez
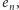 jest równa
jest równa
 -tej sumie częściowej szeregu harmonicznego:
-tej sumie częściowej szeregu harmonicznego:

gdzie
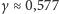 jest stałą Eulera. Jak widać,
jest stałą Eulera. Jak widać,
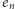 rośnie wraz z
rośnie wraz z
 dość powoli.
dość powoli.
Jak uzyskać ten wynik?
Sposób 1. Jeśli stłuczemy pierwszą
świnkę, to pasujący do niej kluczyk ma równe szanse pojawienia się jako
pierwszy, drugi, itd. Wtedy zadanie sprowadza się do otwarcia pozostałych
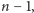
 itd. skarbonek w ten sam sposób. Dlatego
itd. skarbonek w ten sam sposób. Dlatego

Mamy zatem dla
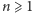 :
:
Z równania (2) wynika, że
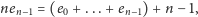 | (3) |
i odjęcie stronami (3) od (1) daje
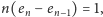 czyli
czyli
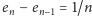 dla
dla
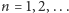 Ostatecznie
Ostatecznie

Jak zwykle, poniewczasie wpadamy na inny pomysł, prowadzący do prostszych rachunków.
Sposób 2. Po stłuczeniu pierwszej świnki mamy
szansę
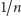 znalezienia tam pasującego do niej kluczyka; wtedy
pozostaje do otwarcia średnio
znalezienia tam pasującego do niej kluczyka; wtedy
pozostaje do otwarcia średnio
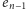 skarbonek. W przeciwnym
razie jesteśmy w stanie otworzyć kolejną skarbonkę (nie musimy jej
tłuc), zatem pozostaje średnio
skarbonek. W przeciwnym
razie jesteśmy w stanie otworzyć kolejną skarbonkę (nie musimy jej
tłuc), zatem pozostaje średnio
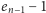 skarbonek do otwarcia. Stąd
równanie:
skarbonek do otwarcia. Stąd
równanie:

Rozwiązując zadanie, korzystaliśmy tak naprawdę z pojęcia warunkowej
wartości oczekiwanej. Przypomnijmy, że zwykła wartość oczekiwana dla
zmiennej losowej przyjmującej skończenie wiele wartości
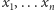 jest
dana wzorem
jest
dana wzorem
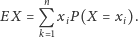 | (4) |
Jeśli teraz wprowadzimy zdarzenie
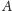 (takie, że
(takie, że
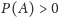 )
i zastąpimy we wzorze (4) zwykłe prawdopodobieństwo przez warunkowe,
otrzymamy średnią wartość
)
i zastąpimy we wzorze (4) zwykłe prawdopodobieństwo przez warunkowe,
otrzymamy średnią wartość
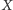 na
na
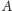 :
:
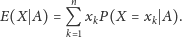 | (5) |
Jeżeli dane jest rozbicie
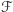 przestrzeni zdarzeń elementarnych
przestrzeni zdarzeń elementarnych
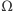 na zdarzenia
na zdarzenia
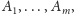 to definiujemy warunkową wartość
oczekiwaną
to definiujemy warunkową wartość
oczekiwaną
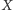 pod warunkiem
pod warunkiem
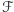 jako zmienną losową, która
przyjmuje wartości
jako zmienną losową, która
przyjmuje wartości
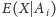 na
na
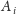 :
:
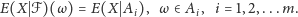 | (6) |
Wtedy można łatwo udowodnić odpowiednik wzoru na prawdopodobieństwo całkowite:
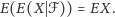 | (7) |
Oto dowód:
Wyrażenie (9) otrzymaliśmy, korzystając z (5). Po zamianie kolejności sumowania równość wyrażeń (10) i (11) wynika oczywiście ze wzoru na prawdopodobieństwo całkowite.
Dwa rozwiązania zadania o średniej liczbie stłuczonych świnek
ilustrują typowe zastosowania wzoru (7), który umożliwia układanie
równań. Mieliśmy do czynienia z dwoma rozbiciami przestrzeni
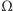 na (wykluczające się!) zdarzenia: w sposobie 1 ze względu na chwilę
pojawienia się kluczyka od pierwszej stłuczonej świnki, w sposobie 2 –
ze względu na to, czy miała w środku swój kluczyk, czy też nie. Można było
łatwo odgadnąć, bez zbędnych formalizmów, czemu są równe średnie
na (wykluczające się!) zdarzenia: w sposobie 1 ze względu na chwilę
pojawienia się kluczyka od pierwszej stłuczonej świnki, w sposobie 2 –
ze względu na to, czy miała w środku swój kluczyk, czy też nie. Można było
łatwo odgadnąć, bez zbędnych formalizmów, czemu są równe średnie