Symetria i prawdopodobieństwo
Pojęcie symetrii przydaje się w rachunku prawdopodobieństwa. Oto kilka przykładów...
Zacznijmy od najprostszego przykładu
Przykład 1. Tasujemy talię
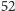 kart do gry, a następnie odkrywamy
kolejno karty z wierzchu talii i każdą z nich po obejrzeniu odkładamy
na spód talii. Jakie jest prawdopodobieństwo tego, że następna karta po
odkryciu asa pik będzie królem kier?
kart do gry, a następnie odkrywamy
kolejno karty z wierzchu talii i każdą z nich po obejrzeniu odkładamy
na spód talii. Jakie jest prawdopodobieństwo tego, że następna karta po
odkryciu asa pik będzie królem kier?
Rozwiązanie. Proste rozwiązanie polega na zauważeniu, że takie
samo jest prawdopodobieństwo tego, iż owa karta będzie np. damą karo
lub dowolną inną z
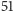 kart w talii różnych od asa pik. Mamy więc
kart w talii różnych od asa pik. Mamy więc
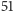 jednakowych prawdopodobieństw, które w sumie dają
jednakowych prawdopodobieństw, które w sumie dają
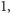 a zatem każde z nich jest równe
a zatem każde z nich jest równe
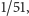 w szczególności szukane
prawdopodobieństwo tego, iż następna karta będzie królem kier.
w szczególności szukane
prawdopodobieństwo tego, iż następna karta będzie królem kier.
Inny prosty przykład dotyczy gry w orła i reszkę.
Przykład 2. Załóżmy, że rzucamy
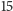 razy symetryczną monetą.
Za każdym razem, gdy wypadnie orzeł, zyskujemy
razy symetryczną monetą.
Za każdym razem, gdy wypadnie orzeł, zyskujemy
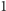 zł, a gdy
wypadnie reszka, tracimy
zł, a gdy
wypadnie reszka, tracimy
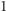 zł. Obliczmy prawdopodobieństwo tego,
iż gra będzie dla nas korzystna, tzn. wśród
zł. Obliczmy prawdopodobieństwo tego,
iż gra będzie dla nas korzystna, tzn. wśród
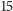 wykonanych rzutów
będzie więcej orłów niż reszek.
wykonanych rzutów
będzie więcej orłów niż reszek.
Rozwiązanie. Zakładamy, że zaczynamy mając
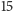 zł, więc nie
grozi nam bankructwo w trakcie gry. Łatwo zauważyć, że wszystkie
możliwe wyniki gry (tzn. piętnastoelementowe ciągi orłów i reszek)
można
połączyć w pary, w których jeden ciąg otrzymamy przez zastąpienie
orłów w drugim ciągu reszkami, a reszek – orłami. Na przykład ciągi
ORRORROORORORRR i ROOROORROROROOO będą tworzyć taką
parę. W ten sposób przyporządkowaliśmy
każdemu zdarzeniu elementarnemu oznaczającemu zwycięstwo zdarzenie
elementarne oznaczające przegraną, a przy tym przyporządkowanie to
jest wzajemnie jednoznaczne („jeden do jednego”) i połączone w pary
zdarzenia elementarne mają jednakowe prawdopodobieństwa, równe
zł, więc nie
grozi nam bankructwo w trakcie gry. Łatwo zauważyć, że wszystkie
możliwe wyniki gry (tzn. piętnastoelementowe ciągi orłów i reszek)
można
połączyć w pary, w których jeden ciąg otrzymamy przez zastąpienie
orłów w drugim ciągu reszkami, a reszek – orłami. Na przykład ciągi
ORRORROORORORRR i ROOROORROROROOO będą tworzyć taką
parę. W ten sposób przyporządkowaliśmy
każdemu zdarzeniu elementarnemu oznaczającemu zwycięstwo zdarzenie
elementarne oznaczające przegraną, a przy tym przyporządkowanie to
jest wzajemnie jednoznaczne („jeden do jednego”) i połączone w pary
zdarzenia elementarne mają jednakowe prawdopodobieństwa, równe
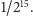 Zatem suma prawdopodobieństw zdarzeń elementarnych
oznaczających zwycięstwo jest równa sumie
prawdopodobieństw zdarzeń elementarnych oznaczających przegraną,
czyli prawdopodobieństwo zwycięstwa jest równe prawdopodobieństwu
przegranej, a że w sumie prawdopodobieństwa te muszą dawać
Zatem suma prawdopodobieństw zdarzeń elementarnych
oznaczających zwycięstwo jest równa sumie
prawdopodobieństw zdarzeń elementarnych oznaczających przegraną,
czyli prawdopodobieństwo zwycięstwa jest równe prawdopodobieństwu
przegranej, a że w sumie prawdopodobieństwa te muszą dawać
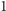 (
(
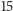 jest liczbą nieparzystą, toteż remis nie jest możliwy),
więc każde z nich jest równe
jest liczbą nieparzystą, toteż remis nie jest możliwy),
więc każde z nich jest równe
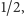 w szczególności szukane
prawdopodobieństwo zwycięstwa.
w szczególności szukane
prawdopodobieństwo zwycięstwa.
Powyższy przykład może wydawać się zbyt prosty. Rozważmy więc zmodyfikowaną wersję tego problemu
Przykład 3.
Gramy na tych samych zasadach, ale tym razem zaczynamy grę, mając tylko
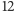 zł i jeśli podczas gry nasz kapitał stopnieje do zera, bankrutujemy.
Z jakim prawdopodobieństwem unikniemy bankructwa w ciągu
zł i jeśli podczas gry nasz kapitał stopnieje do zera, bankrutujemy.
Z jakim prawdopodobieństwem unikniemy bankructwa w ciągu
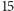 rzutów monetą?
rzutów monetą?
Rozwiązanie. Umówmy się, że w przypadku bankructwa i tak wykonamy brakujące rzuty. Być może krupier prowadzący grę jest wspaniałomyślny i zgodzi się uwzględnić owe rzuty, niejako przejściowo nas kredytując, jeśli dzięki temu na końcu gry mielibyśmy znów dodatni kapitał. Mamy więc trzy wzajemnie się wykluczające zdarzenia losowe:
-
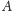 – nie zbankrutowaliśmy,
– nie zbankrutowaliśmy,
-
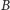 – zbankrutowaliśmy, ale wspaniałomyślność
krupiera może nam pomóc,
– zbankrutowaliśmy, ale wspaniałomyślność
krupiera może nam pomóc,
-
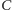 – zbankrutowaliśmy i nawet przejściowe kredytowanie
nie pomoże.
– zbankrutowaliśmy i nawet przejściowe kredytowanie
nie pomoże.
Oczywiście
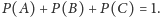 Wykażemy teraz, że
Wykażemy teraz, że
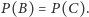 W tym celu połączymy możliwe wyniki gry (tzn. piętnastoelementowe ciągi
orłów i reszek) odpowiadające zdarzeniom
W tym celu połączymy możliwe wyniki gry (tzn. piętnastoelementowe ciągi
orłów i reszek) odpowiadające zdarzeniom
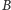 i
i
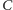 w pary. Zrobimy
to w następujący sposób – jeśli jakiś ciąg wyników oznacza bankructwo
w pewnym momencie gry, to wszystkie reszki występujące po tym momencie
zamieniamy na orły, a orły – na reszki. Tak utworzony ciąg łączymy w parę
z ciągiem wyjściowym.
w pary. Zrobimy
to w następujący sposób – jeśli jakiś ciąg wyników oznacza bankructwo
w pewnym momencie gry, to wszystkie reszki występujące po tym momencie
zamieniamy na orły, a orły – na reszki. Tak utworzony ciąg łączymy w parę
z ciągiem wyjściowym.
Na przykład ciąg RRRRRRRRRRRR-OOR połączymy w parę z ciągiem
RRRRRRRRRRRR-RRO. W ten sposób ustalamy wzajemnie jednoznaczne
przyporządkowanie między zdarzeniami elementarnymi składającymi się
na
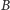 i zdarzeniami elementarnymi składającymi się na
i zdarzeniami elementarnymi składającymi się na
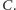 Istotnie,
owa zamiana spowoduje zmianę znaku w końcowym rezultacie gry (przy
założeniu, że krupier okaże się wspaniałomyślny), a ponieważ zaczynamy
grę mając
Istotnie,
owa zamiana spowoduje zmianę znaku w końcowym rezultacie gry (przy
założeniu, że krupier okaże się wspaniałomyślny), a ponieważ zaczynamy
grę mając
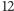 zł, końcowy rezultat z pewnością będzie liczbą nieparzystą
(bo
zł, końcowy rezultat z pewnością będzie liczbą nieparzystą
(bo
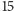 jest liczbą nieparzystą, a parzystość naszego kapitału zmienia się
w każdej turze gry, niezależnie od tego, co wypadnie), a więc nie będzie
zerem. Zauważmy teraz, że prawdopodobieństwo zdarzenia
jest liczbą nieparzystą, a parzystość naszego kapitału zmienia się
w każdej turze gry, niezależnie od tego, co wypadnie), a więc nie będzie
zerem. Zauważmy teraz, że prawdopodobieństwo zdarzenia
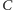 łatwo
obliczyć:
łatwo
obliczyć:

bo zajście zdarzenia
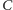 równoważne jest temu, iż wszystkie rzuty albo
wszystkie oprócz jednego dały jako wynik reszkę, a temu odpowiada
dokładnie
równoważne jest temu, iż wszystkie rzuty albo
wszystkie oprócz jednego dały jako wynik reszkę, a temu odpowiada
dokładnie
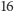 zdarzeń elementarnych:
zdarzeń elementarnych:
RRRRRRRRRRRRRRR,
ORRRRRRRRRRRRRR, RORRRRRRRRRRRRR, ..., RRRRRRRRRRRRROR,
RRRRRRRRRRRRRRO,
z których każde ma prawdopodobieństwo
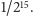 Jeśli w dokładnie
Jeśli w dokładnie
 rzutach wypadną reszki, to grę
(kredytowaną) zakończymy z kapitałem
rzutach wypadną reszki, to grę
(kredytowaną) zakończymy z kapitałem

a
 będzie liczbą dodatnią tylko wtedy, gdy
będzie liczbą dodatnią tylko wtedy, gdy
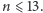 Skoro
Skoro
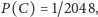 to i
to i
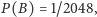 a zatem
a zatem

Z kwotą
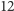 zł możemy więc siadać do
zł możemy więc siadać do
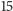 tur gry w orła i reszkę,
nie obawiając się zbytnio bankructwa, nawet jeśli nie jesteśmy pewni
wspaniałomyślności krupiera.
tur gry w orła i reszkę,
nie obawiając się zbytnio bankructwa, nawet jeśli nie jesteśmy pewni
wspaniałomyślności krupiera.
Nawet w pozornie niesymetrycznej sytuacji można odnaleźć motywy oparte na symetrii. Dobrze ilustruje to następujące zadanie.
Zadanie. W probówce znajduje się dziesięć bakterii białych i dwadzieścia bakterii czarnych. Co minutę jedna z bakterii dzieli się na dwie o takim samym jak ona kolorze, przy czym wszystkie bakterie znajdujące się wówczas w probówce mają jednakowe szanse na podział. Po godzinie w naczyniu będzie 90 bakterii. Wylosujmy jedną z nich. Jakie jest prawdopodobieństwo tego, że będzie ona biała?
Rozwiązanie. Załóżmy, że każda bakteria jest w nieco innym
odcieniu
(bieli lub czerni) i podczas podziału odcień koloru jest zachowywany.
Prawdopodobieństwo tego, że wylosowana przez nas bakteria ma dany
odcień, wynosi
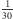 (wszystkie odcienie są „równouprawnione”).
Ponieważ 10 spośród odcieni jest białych, szansa, iż wylosujemy białą
bakterię, jest równa
(wszystkie odcienie są „równouprawnione”).
Ponieważ 10 spośród odcieni jest białych, szansa, iż wylosujemy białą
bakterię, jest równa
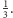
Warto przypomnieć jeszcze jeden przykład świadczący o roli symetrii w rachunku prawdopodobieństwa. Maxwell, badając rozkład wektora prędkości cząsteczek gazu, zauważył, że rozkład ten powinien mieć symetrię obrotową (tzn. nie powinno go zmieniać obrócenie układu współrzędnych), a współrzędne tego wektora powinny być niezależnymi zmiennymi losowymi. Tu kończą się założenia wywodzące się z fizyki, a do akcji wkracza matematyka – okazuje się, że wektor losowy, spełniający powyższe dwa warunki, musi mieć rozkład gaussowski. Wynik ten, uzyskany na drodze czysto matematycznego rozumowania, podobno całkiem dobrze zgadza się z danymi doświadczalnymi.
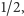 a nie
wtedy, gdy ma ona oś symetrii, a więc np. orła po obu stronach...
a nie
wtedy, gdy ma ona oś symetrii, a więc np. orła po obu stronach...
 połączone jest w parę z dokładnie jednym zdarzeniem
elementarnym z
połączone jest w parę z dokładnie jednym zdarzeniem
elementarnym z
 i vice versa.
i vice versa.