Metoda probabilistyczna
Jak pokazać, że istnieje obiekt o pewnych własnościach? Najprościej jest podać bezpośrednią konstrukcję, jednak często jest to bardzo trudne (a czasem w ogóle niewykonalne). Jednym ze sposobów ominięcia tego problemu jest tak zwana metoda probabilistyczna...
Polega ona na tym, że w celu wykazania, iż zbiór poszukiwanych obiektów jest niepusty, dowodzimy, że ma dodatnie prawdopodobieństwo. W praktyce często się wykazuje, że to prawdopodobieństwo jest bliskie 1, czyli „typowy” obiekt ma poszukiwaną własność.
Spróbujmy na początek dowieść istnienia funkcji ciągłej na pewnym przedziale i nieróżniczkowalnej w żadnym punkcie dziedziny. W tym przypadku można podać wzór, jednak nie będzie on ani łatwy do zweryfikowania, ani specjalnie przyjemny. Prościej jest zauważyć, że takie funkcje są znane każdemu probabiliście – to trajektorie procesu Wienera. Okazuje się, że wszystkie są ciągłe, a z prawdopodobieństwem 1 nigdzie nieróżniczkowalne.
Rozważmy następujący
Problem. Dla
jakich
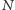 i
i
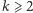 zbiór
zbiór
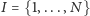 da się podzielić
na dwa podzbiory
da się podzielić
na dwa podzbiory
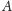 i
i
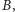 z których żaden nie zawiera
z których żaden nie zawiera
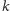 -elementowego podciągu arytmetycznego?
-elementowego podciągu arytmetycznego?
Dokładna odpowiedź na to pytanie nie jest znana, wykażemy tutaj, że
dla
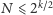 taki podział istnieje. Rozważmy losowy podział –
wyobraźmy sobie, że rzucamy
taki podział istnieje. Rozważmy losowy podział –
wyobraźmy sobie, że rzucamy
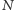 symetrycznymi monetami i jeśli na
symetrycznymi monetami i jeśli na
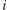 -tej monecie wypadł orzeł, to liczbę
-tej monecie wypadł orzeł, to liczbę
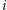 przydzielamy do zbioru
przydzielamy do zbioru
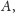 a jeśli reszka, to do zbioru
a jeśli reszka, to do zbioru
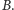 Prawdopodobieństwo tego,
że ustalony ciąg arytmetyczny
Prawdopodobieństwo tego,
że ustalony ciąg arytmetyczny
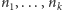 jest zawarty w zbiorze
jest zawarty w zbiorze
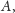 wynosi
wynosi
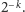 Wszystkich
Wszystkich
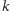 elementowych ciągów
arytmetycznych o wartościach w
elementowych ciągów
arytmetycznych o wartościach w
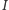 jest mniej niż
jest mniej niż
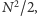 stąd
prawdopodobieństwo tego, że
stąd
prawdopodobieństwo tego, że
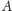 zawiera pewien ciąg arytmetyczny
długości
zawiera pewien ciąg arytmetyczny
długości
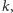 jest mniejsze niż
jest mniejsze niż
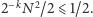 Podobnie możemy
rozumować dla zbioru
Podobnie możemy
rozumować dla zbioru
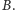 Czyli z dodatnim prawdopodobieństwem oba
zbiory
Czyli z dodatnim prawdopodobieństwem oba
zbiory
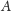 i
i
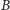 nie zawierają ciągu arytmetycznego! Ambitny
Czytelnik może spróbować skonstruować deterministyczny podział, np. dla
nie zawierają ciągu arytmetycznego! Ambitny
Czytelnik może spróbować skonstruować deterministyczny podział, np. dla
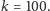
W podanym wyżej przykładzie moglibyśmy jeszcze obejść się bez rachunku prawdopodobieństwa, wykorzystując tylko zliczanie elementów. Jednak w bardziej zaawansowanych problemach jest to niemożliwe. Obszerny i burzliwie rozwijający się dział kombinatoryki poświęcony jest badaniu grafów losowych. Tutaj konstrukcje probabilistyczne prowadzą do budowania grafów o rozmaitych ciekawych własnościach. Grafów o podobnych własnościach w wielu przypadkach nie można opisać w bezpośredni sposób. Najciekawsze konstrukcje bazują na podejściu łączącym elementy losowe i deterministyczne.
Metoda losowa znajduje zastosowanie nie tylko w kombinatoryce. Za jej pomocą
Dvoretzky wykazał zaskakujące twierdzenie dotyczące wysokowymiarowych ciał
wypukłych. Mianowicie, każdy
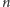 -wymiarowy, środkowosymetryczny
wielościan ma co najmniej
-wymiarowy, środkowosymetryczny
wielościan ma co najmniej
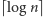 -wymiarowy centralny przekrój bliski
kuli (tzn. stosunek promieni kuli wpisanej i opisanej na tym przekroju jest
nieduży). Podobnie każdy
-wymiarowy centralny przekrój bliski
kuli (tzn. stosunek promieni kuli wpisanej i opisanej na tym przekroju jest
nieduży). Podobnie każdy
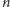 -wymiarowy wielościan ma prawie kulisty
-wymiarowy wielościan ma prawie kulisty
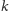 -wymiarowy rzut. Co więcej, dla wielu brył można znacząco
zwiększyć wymiar takiego przekroju czy rzutu. Kashin wykazał, że losowy
-wymiarowy rzut. Co więcej, dla wielu brył można znacząco
zwiększyć wymiar takiego przekroju czy rzutu. Kashin wykazał, że losowy
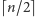 -wymiarowy rzut
-wymiarowy rzut
 -wymiarowej kostki jest z ogromnym
prawdopodobieństwem bliski kuli. Jednak, mimo że wiadomo, iż rzuty kostki
na „typową”
-wymiarowej kostki jest z ogromnym
prawdopodobieństwem bliski kuli. Jednak, mimo że wiadomo, iż rzuty kostki
na „typową”
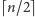 wymiarową przestrzeń są kuliste, nie jest
do dzisiejszego dnia znana żadna deterministyczna konstrukcja takich
rzutów.
wymiarową przestrzeń są kuliste, nie jest
do dzisiejszego dnia znana żadna deterministyczna konstrukcja takich
rzutów.
Argumenty losowe są obecne również w dowodzie niedawno wykazanego przez Greena i Tao twierdzenia, mówiącego, że istnieją dowolnie długie ciągi arytmetyczne złożone z liczb pierwszych.
Powyższa lista, mimo iż bardzo wybiórcza, powinna zasygnalizować Czytelnikowi, że losowe konstrukcje coraz częściej występują w dowodach rezultatów z kombinatoryki, analizy, geometrii czy teorii liczb. Są także inne ważne, niekonstruktywne sposoby dowodzenia, że zbiory są duże, np. z użyciem aparatu topologicznego zamiast probabilistycznego. Ale to temat na inną opowieść.
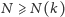 taki
podział nie istnieje. Optymalne wartości
taki
podział nie istnieje. Optymalne wartości
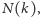 znane tylko dla
małych
znane tylko dla
małych
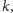 to
to
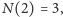
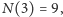
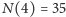 i
i
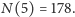 Rozumowanie poniżej pokazuje, że
Rozumowanie poniżej pokazuje, że