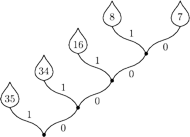
Konstruujemy drzewko. Najpierw łączymy dwa „liście” o najmniejszej wadze (D i E), które będą w efekcie wyrastać ze wspólnego węzła. Otrzymujemy nową listę wag: 35, 34, 16, 15. Następnie łączymy dwie najmniejsze wagi i powtarzamy procedurę, dopóki się da. Rezultat widać na rysunku, drzewko sugeruje (mamy nadzieję) sposób zadawania pytań. Jeśli odpowiedź „tak” oznaczymy cyfrą 1, a odpowiedź „nie” cyfrą 0, to ciągi odpowiedzi (kody) identyfikujące wszystkie imiona będą wyglądać jak w tabeli na marginesie.

Do identyfikacji potrzebujemy średnio

pytania na osobę, podczas gdy entropia  odpowiedniego rozkładu prawdopodobieństwa jest równa 2,04. Przypominamy, że

gdzie w naszym przypadku 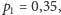 …,  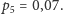Widzimy, że spełniona jest nierówność z poprzedniego odcinka:

Przedstawiona metoda pochodzi od Huffmana. Można udowodnić, że średniej liczby pytań nie da się zmniejszyć.

Wyobraźmy sobie, że mamy tekst, w którym występują wyłącznie litery A, B, C, D i E z podanymi wcześniej częstościami. Gdybyśmy chcieli go zakodować za pomocą ciągu cyfr dwójkowych, czyli zer i jedynek, to, na przykład, słowo BABA przybrałoby postać 011011. Kod o stałej długości wymagałby trzech cyfr dwójkowych (bitów) na znak. Kod Huffmana wymaga tylko 2,11 bita na znak. Rzut oka do tabeli pozwala stwierdzić, że więcej oszczędzamy na często występujących symbolach A i B o krótkich kodach, niż tracimy na rzadkich symbolach D i E o długich kodach.

Kod Huffmana jest w pewnym sensie optymalny, ale w jakim? Jeśli kodujemy pojedyncze znaki, to liczby bitów na znak nie da się już zmniejszyć. Stąd oczywiste zastosowania w programach archiwizujących pliki komputerowe. Z drugiej strony kodowanie tekstu BA BA (powtórzone milion razy) metodą Huffmana jest, delikatnie mówiąc, nieoptymalne. W języku naturalnym takie teksty zdarzają się rzadko, choć, na przykład, w zapisie cyfrowym fotografii analogiczne ciągi nie są niczym dziwnym. Skoro jednak mowa o języku naturalnym, to doskonale wiadomo, że żaden język nie przypomina ciągu symboli generowanych niezależnie z ustalonymi częstościami. Przeciwnie, znając część wyrazu można na ogół odtworzyć całość.

Nad oszacowaniem faktycznej entropii tekstu w bitach na znak zastanawiał się już twórca teorii informacji, Claude Shannon. Jeśli wziąć pod uwagę tylko częstości występowania liter w języku angielskim, to wynosi ona 2,14 bita na znak. Shannon zaproponował zadziwiająco prostą i pomysłową metodę szacowania faktycznej entropii tekstu: odczytywał kolejne litery, a druga osoba zgadywała dalszy ciąg. Okazało się, że entropia zawiera się w granicach 0,6–1,3 bita na znak. Jak wykorzystać ten fakt przy kodowaniu? Chyba będziemy musieli zastanowić się nad tym w przyszłości.

Czasem znając pierwszą literę tekstu, można odtworzyć całkiem pokaźny fragment, jak w przypadku artykułu z pierwszej strony „Trybuny Ludu” z lat siedemdziesiątych ubiegłego stulecia:
„Pierwszy sekretarz KC PZPR Edward Gierek przebywał wczoraj z gospodarską wizytą w Zakładach Mięsnych im. Feliksa Dzierżyńskiego w Mławie...” – itd. w tym stylu. Przykłady współczesne tekstów o zawartości informacyjnej 0 bitów na znak każdy dośpiewa sobie sam.