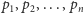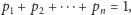
W teorii prawdopodobieństwa może lepiej mówić o niepewności lub różnorodności, związanej z rozkładem. Dla prostoty zajmiemy się rozkładami dyskretnymi: niech liczby wyznaczają rozkład prawdopodobieństwa, zatem  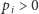  dla 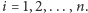Wartości liczbowe skojarzone z prawdopodobieństwami 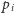 są zupełnie nieistotne; zresztą nie muszą to być liczby, a mogą to być, na przykład, imiona pań, które pojawiły się na pewnym protokole egzaminacyjnym. Imion tych było 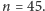 Gdybyśmy chcieli odgadnąć, jak ma na imię losowo wybrana dziewczyna, znając możliwe imiona i zadając pytania, na które można odpowiedzieć tak/nie, to 5 pytań mogłoby nie wystarczyć ( 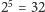), ale 6 pytań wystarczy na pewno, bo wszystkich możliwych ciągów odpowiedzi jest 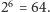 Czytelnik na pewno wie, jak rozsądnie zadawać pytania, żeby ich średnia liczba mieściła się pomiędzy 5 i 6.

Kluczową rolę w tym rozumowaniu odgrywała nierówność

równoważna z

czyli

Można zatem podejrzewać, że logarytm dwójkowy z liczby możliwości  faktycznie jakoś mierzy różnorodność. Ale przecież nie wzięliśmy pod uwagę tego, że imiona występują z rozmaitymi częstościami. W naszym protokole cztery najczęstsze imiona to Anna – 14%, Joanna, Katarzyna i Magdalena – po 8%. Jak można z tego skorzystać przy zadawaniu pytań?

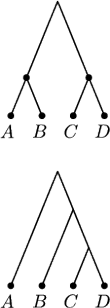
Rozważmy prostszą sytuację. Jeśli są tylko cztery imiona: Agnieszka, Barbara, Celina i Dorota, pojawiające się jednakowo często, to średnio (i zawsze) potrzebne są 2 pytania. Niech teraz A ma częstość 50%, B – 25%, C i D – po 12,5%. Każdy widzi, że z prawdopodobieństwem 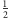 wystarczy jedno pytanie, 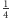 – dwa, 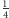 – trzy. Średnio jest 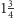 pytania.

Zapiszmy tę średnią tak:

Średnia liczba pytań okazała się równa

i to jest właśnie entropia rozkładu prawdopodobieństwa. Można udowodnić, że

(*)

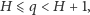zatem entropia 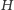 jest dolnym ograniczeniem średniej liczby pytań 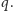 Entropia jest największa, gdy wszystkie 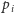 są równe. Wynika to z wklęsłości funkcji 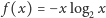 i nierówności Jensena:

gdzie liczby 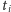 są dodatnie i dają w sumie 1.

W takim razie

Jasne jest, że 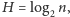 gdy  

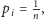
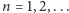
W przypadku 45. imion z protokołu faktyczna entropia jest równa 4,76, podczas gdy maksymalna możliwa to 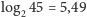; niewielka różnica obu liczb świadczy o dużej fantazji rodziców przy nadawaniu imion dziewczynkom.

Pozostaje pytanie, czy jest prosty sposób na zadawanie pytań tak, by spełniona była nierówność (*). O tym za miesiąc – doprowadzi nas to do tak zwanego kodu Huffmana (dajemy słowo honoru, że Leonardo da Vinci nie mógł go znać).