W takim sformułowaniu zadanie to umieścił w pracy Luca Pacioli (od roku 1475 franciszkanin z Borgo San Sepolcro w środkowych Włoszech). Wiadomo, że znane było ono znacznie wcześniej.

Pacioli proponuje podział proporcjonalny do liczby zebranych punktów. Rozwiązanie to spotkało się z krytyką Tartaglii (rozdz. 20 pt. „Błąd brata Luki z Borgo”). Tartaglia proponuje podzielić pulę, do której każdy włożył 22 dukaty, w następujący sposób:

Gracz, który uzyskał 50 punktów, dostanie 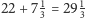dukata, drugi zaś 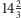dukata.

Tartaglia uważał, że odchylenie od połowy puli ma być proporcjonalne do różnicy zebranych punktów. Wtedy gracz, który zebrał więcej punktów, otrzymuje połowę puli plus sumę wyliczoną według tej zasady.

Jeszcze inny sposób podziału proponuje Cardano. Jeśli gra się do 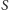punktów, a gracze zebrali odpowiednio 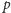i 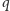 punktów, to pulę dzielimy w stosunku

Zdaje się, że nie było w zwyczaju uzasadnianie podawanych reguł. Dopiero Pascal w liście do Fermata z roku 1654, rozpatrując przypadek gry do trzech wygranych przy stanie 2:1, przedstawia korespondentowi eleganckie rozumowanie:

Każdy z graczy włożył do puli 32 pistole. Gdyby w następnej partii pierwszy gracz wygrał, wziąłby 64 pistole. Gdyby przegrał, przy stanie 2:2 wziąłby 32 pistole. Ma zatem gwarantowane 32 pistole, a pozostałe 32 mogą równie dobrze przypaść jemu, jak i partnerowi – szanse są równe, więc należy podzielić się po połowie.

Pula zostaje zatem podzielona w stosunku 48:16, czyli 3:1. Okazuje się, że taki jest stosunek prawdopodobieństw wygranej dla obydwu graczy. Wyraźnie widać to w rozumowaniu Fermata (ten list Fermata zaginął, ale zachowała się odpowiedź Pascala) dotyczącym przypadku, gdy pierwszemu graczowi brakuje dwóch punktów, a drugiemu – trzech. Gra rozstrzygnie się zatem najpóźniej po czterech partiach. Fermat układa tablicę 16 możliwych wyników czterech partii (choć gra może zakończyć się wcześniej), z której widać, że pierwszemu graczowi sprzyja 11 wyników, a drugiemu 5. Wobec tego 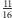puli otrzymuje pierwszy gracz, a resztę drugi.

Jaką przewagę nad innymi sposobami podziału puli ma reguła podziału według prawdopodobieństw wygranej? Czy nie jest przypadkiem równie arbitralna, jak poprzednie?

Wyobraźmy sobie, że widzimy Jana i Piotra w sytuacji rozważanej przez Fermata: Janowi brak dwóch punktów, Piotrowi trzech, w puli jest 16 pistoli. Muszą zakończyć grę, bowiem Jan ma niecierpiącą zwłoki sprawę do załatwienia. Żaden z nich nie zna sposobu Fermata i właśnie Jan zgodził się wziąć 10 pistoli, pozostawiając Piotrowi 6. Proponujemy Janowi 10 pistoli (a może nawet 10 i pół) za odstąpienie prawa do dokończenia gry.

Wszyscy są zadowoleni, my wygrywamy średnio 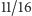puli, czyli 11 pistoli.

Krótko mówiąc, Jan miał papier wartościowy, który wycenił na 10 pistoli. Znając jego prawdziwą wartość, mogliśmy go odkupić z zyskiem (dokładniej: jeśli operację powtórzymy wiele razy, to prawie na pewno zarobimy). Finansiści nazywają taką operację arbitrażem. Gdyby Jan kierował się regułą Fermata, arbitraż byłby niemożliwy – nikt nie mógłby zarobić na niewiedzy graczy.

Pojęcie średniej wygranej pojawiło się kilka lat później w pracy Huygensa O rachubach w grze w kości pod postacią nadziei matematycznej. We współczesnej terminologii jest to wartość oczekiwana (albo średnia) zmiennej losowej.