Prawdopodobieństwem warunkowym zdarzenia pod warunkiem, że zaszło zdarzenie (o dodatnim prawdopodobieństwie) nazywamy liczbę

Znane są liczne przykłady prostych zadań, w których obliczenie prawdopodobieństwa warunkowego daje zaskakujący wynik. Punktem wyjścia będzie umiarkowane pod tym względem

Teraz nieco bardziej zaskakujące

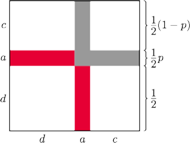
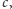
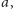
Ostatecznie chłopiec musi mieć jakieś imię – czy zatem dowiedzieliśmy się czegoś istotnie nowego, co mogłoby zmienić szanse badanego zdarzenia? Zobaczmy. Mamy teraz trzy kategorie dzieci ( 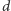) i dziewięć zdarzeń elementarnych. Antoni to rzadkie imię – chłopiec ma szansę 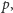że je otrzyma. Wbrew utartym zwyczajom niech 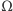będzie kwadratem jednostkowym – będziemy obliczać pola figur.

---

Szukane prawdopodobieństwo to stosunek pola części krzyża pomalowanej na szaro do pola całego krzyża:

Ciężko w to uwierzyć; błędu rachunkowego chyba nie ma. Dla 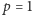(każdy chłopiec to Antoni) uzyskujemy odpowiedź z przykładu 1. Ale i tak coś jest zasadniczo nie w porządku.

Zadanie to ukazało się w książce, napisanej przez psychologa, badającego reakcje ludzi na takie dziwne zadania. Zostało ubrane w tekst o osiedlu, na którym mieszkają wyłącznie rodziny z dwojgiem dzieci. Widząc ojca z synem na spacerze, dowiadujemy się, że syn ma na imię Antoni, etc.

Sprecyzujmy zatem warunki doświadczenia. Niech dzieci będą wyprowadzane na spacer w wyniku sprawiedliwego (inaczej rodzice ryzykują awanturę) losowania. Zbiór zdarzeń elementarnych będzie musiał zostać wzbogacony – oto typowe zdarzenie elementarne: 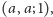co czytamy: młodszy Antoni, starszy Antoni, na spacerze młodszy.

Teraz okazuje się, że już jest normalnie: jeśli na spacerze jest Antoni, to szansa, że w domu została dziewczynka, wynosi 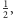chłopiec (nie Antoni) – 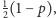wreszcie Antoni – 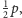zgodnie z częstościami występowania wymienionych kategorii dzieci. Tak powinno być, ponieważ dokonujemy tu losowania dwuetapowego – najpierw rodziny, potem dziecka.

Powyższe wyniki można uzyskać, wypisując pracowicie zdarzenia elementarne, nic dziwnego więc, że wolimy wzór Bayesa.

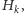
Niech na przykład 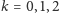oznacza zdarzenie „w rodzinie jest 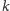dzieci o drugim imieniu Antoni”, 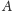 zaś – „Antoni jest na spacerze”. Obliczamy

Wobec tego w jakich warunkach można się spodziewać wyniku 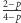? Może w takich:
w urzędzie gminy jest kartoteka z danymi o rodzinach z dwójką dzieci. Znajomy urzędnik wyjmuje losowo kartę i informuje nas, że w rodzinie jest syn o drugim imieniu Antoni. My oceniamy szansę, że w rodzinie jest dwóch synów (być może obaj o drugim imieniu Antoni).