Nie chcemy Was namawiać aż do tak radykalnych poglądów, spróbujemy jednak zachęcić do zabawy w „matematykę empiryczną”. To też jakieś oblicze królowej nauk, więc można mu się od czasu do czasu przyjrzeć.

Prawo wielkich liczb

Już sama nazwa „prawo” zamiast „twierdzenie” przywodzi na myśl fizykę. Istotnie, jest to wynik matematyczny bliski sercom doświadczalników. O co w nim chodzi?

Wyobraźmy sobie, że w pewnym eksperymencie losowym mamy jednakowo prawdopodobnych wyników. Wyniku pojedynczego eksperymentu nie da się przewidzieć. Jednak prawo wielkich liczb mówi, że gdy eksperyment powtórzymy 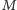razy, to gdy 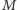jest bardzo duże, każdy z możliwych wyników pojawi się w dobrym przybliżeniu 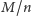razy. Możemy teraz – mając do czynienia z jakąś grą losową – postępować na dwa sposoby do wyboru. Po pierwsze możemy wypisać wszystkie możliwe wyniki pojedynczego eksperymentu, a potem policzyć, jaki procent spośród nich zajmują te, które sprzyjają naszej wygranej. Stąd będziemy wiedzieli, czy opłaca się grać, czy nie, zanim zaczęliśmy grę. Drugi sposób to pójść na żywioł i ekperymentować, grając w grę wiele, wiele razy...

Najprostszy przypadek jest wtedy, gdy 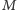razy rzucamy monetą. W jednym ekperymencie (pojedynczy rzut) możliwe są 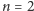zdarzenia: orzeł lub reszka. Prawo wielkich liczb mówi, że gdy np. 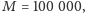to w przybliżeniu 50 000 razy wypadnie orzeł. Bardzo ważne jest tu słowo „w przybliżeniu”. Szansa, że orzeł wypadnie dokładnie 50 000 razy jest niemal zerowa, natomiast, szansa tego, że wypadnie w 49 do 51 procentach wypadków (czyli od 49 000 do 51 000 razy) jest właściwie równa 1.

Eksperyment 1: Koza i samochód.

W pewnym teleturnieju (o którym zresztą niedawno pisaliśmy w Delcie) w kulminacyjnym punkcie prowadzący pokazuje troje drzwi i mówi, że za jednymi znajduje się samochód, natomiast za pozostałymi dwoma coś w porównaniu z samochodem bezwartościowego, na przykład koza. Uczestnik zostaje poproszony o wybór drzwi, ale wybrane przez niego drzwi jeszcze się nie otwierają, prowadzący zaś otwiera jedne z dwojga pozostałych drzwi. Oczywiście pokazuje się w nich koza. Uczestnik ma wtedy ostatnią szansę na zmianę swojej decyzji. Czy powinien to zrobić? Rozwiążmy problem empirycznie.

Będą potrzebne trzy jednakowe kubki, jakiś mały fant (mieszczący się pod kubkiem), trochę monet lub zapałek oraz cierpliwość. Do gry potrzeba minimalnie trzech osób, jedna do roli krupiera, jedna do gry strategią 1: zawsze zmieniaj wybór; druga do gry strategią 2: nigdy nie zmieniaj wyboru. Krupier postępuje tak, jak prowadzący w teleturnieju, ukrywając fant pod jednym z kubków i gra się rozpoczyna. Za każdą wygraną (czyli odkrycie kubka z fantem) gracz otrzymuje monetę (zapałkę lub inny licznik). Teraz potrzebna jest cierpliwość: żeby otrzymać jakieś sensowne wyniki, należy grać dość długo, jednak już po około pięćdziesięciu rundach zarysowuje się różnica w ilości zgromadzonych monet przez graczy grającymi różnymi metodami.

Spróbujcie po wykonaniu odpowiedniej liczby eksperymentów określić, jaka jest w przybliżeniu szansa na zwycięstwo w grze, gdy gramy strategią nr 1 i gdy gramy strategią nr 2. Czy potraficie też wypisać wszystkie możliwe wyniki pojedynczego eksperymentu? Czy „teoria” zgadza się z wynikami doświadczalnymi?

Eksperyment 2: Wykrywacz kłamstw.

Jak powszechnie wiadomo kłamstwo ma krótkie nogi. Ale gdyby tak trochę pokłamać dla celów naukowych? Podczas VII Festiwalu Nauki zaproponowaliśmy uczniom następującą grę, którą z powodzeniem możesz powtórzyć ze swoimi znajomymi. Podziel ich na dwie drużyny (mogą być jednoosobowe), które uzbrojone w kartkę, długopis i monetę będą wychodzić z Twojego pokoju. Za drzwiami drużyny umawiają się, która z nich będzie grała uczciwie, a która będzie oszukiwać. Drużyna uczciwa rzuca 100 razy symetryczną monetą i zapisuje ciąg kolejnych wyników np.: 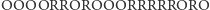gdzie 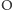 oznacza wyrzucenie orła, a 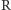 – wyrzucenie reszki. Drużyna, która oszukuje, wcale nie rzuca monetą, tylko wymyśla ciąg stu wyników i też go zapisuje. Po wykonaniu zadania obie drużyny wracają do pokoju i przekazują kartki z wynikami osobie prowadzącej grę, czyli Tobie.

Teraz przyjrzyj się uważnie wynikom. Jeśli na którejś z kartek nie będzie sześciu kolejno wyrzuconych orłów lub reszek mów śmiało, że drużyna kłamała. W pozostałych przypadkach… trudno, musisz zgadywać. Okaże się – o ile Twoi znajomi wykażą się dostateczną cierpliwością, by zagrać z Tobą kilka lub kilkanaście razy – że zadziwiająco często odróżnisz oszustów od uczciwych. Dlaczego? Otóż wśród możliwych wyników stukrotnego rzutu monetą zdecydowana większość zawiera co najmniej 6-krotne serie orłów. O tym jednak „nie wie” nasza intuicja, która „oszustom” błędnie podpowiada, by nie wpisywali więcej, niż pięciu orłów z rzędu.

W tym miejscu warto spostrzec, że wypisanie wszystkich możliwych wyników 100-krotnego rzutu monetą nie da się właściwie zrealizować (jest 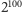możliwości), trzeba więc sprytnie i trickowo wyliczać, ile serii ma co najmniej 6 orłów z rzędu lub... przeprowadzić trochę eksperymentów.