Konkurs prac uczniowskich
Jak matematyk rzuca igłą?
Jednym z najbardziej znanych zagadnień prawdopodobieństwa geometrycznego
jest problem igły Buffona. Treść tego zadania zna wiele osób, które, nawet
jeśli nie znają sposobu rozwiązania, to wiedzą, że jest ono związane z liczbą
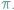
Istotnie, pozwala to (w odpowiednim modelu matematycznym) wyznaczyć
przez wykonanie serii doświadczeń wartość liczby
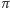 z dokładnością
zależną od liczby doświadczeń.
z dokładnością
zależną od liczby doświadczeń.
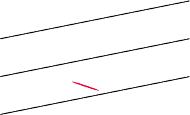
Rys. 1 Igła rzucona na podłogę z desek.
Problem. Na podłogę wyłożoną identycznymi, nieskończenie długimi deskami jedna obok drugiej (tak że nie ma między nimi przerw) rzucamy igłę o nierozróżnialnych końcach. Jakie jest prawdopodobieństwo, że igła będzie dotykać miejsca styku dwóch desek?
Nie napiszę kolejny raz standardowego rozwiązania – jest ono wystarczająco rozpowszechnione. Zastanówmy się nad innym podejściem do tego problemu.
Niech
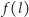 oznacza średnią liczbę przecięć odcinka o długości
oznacza średnią liczbę przecięć odcinka o długości
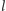 z prostymi rodziny
z prostymi rodziny
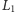 przy jednym rzucie. Zauważmy, że jeśli nasz
odcinek dowolnie podzielimy na dwie części o długości
przy jednym rzucie. Zauważmy, że jeśli nasz
odcinek dowolnie podzielimy na dwie części o długości
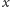 i
i
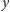 (oczywiście
(oczywiście
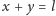 oraz
oraz
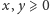 ), to wartość oczekiwana
liczby przecięć, liczona dla mniejszych fragmentów, po zsumowaniu da
wartość oczekiwaną liczby przecięć dla odcinka wyjściowego:
), to wartość oczekiwana
liczby przecięć, liczona dla mniejszych fragmentów, po zsumowaniu da
wartość oczekiwaną liczby przecięć dla odcinka wyjściowego:
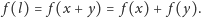 | (1) |
Dodajmy jeszcze jedno proste spostrzeżenie:
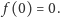
Podłogę możemy zastąpić płaszczyzną podzieloną rodziną prostych
równoległych
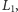 reprezentujących miejsca styku dwóch desek.
Odległość między dwiema kolejnymi prostymi jest równa
reprezentujących miejsca styku dwóch desek.
Odległość między dwiema kolejnymi prostymi jest równa
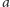 – szerokości deski. Jeżeli przyjmiemy realistyczne założenia, że grubość
igły jest dużo mniejsza od szerokości deski oraz że igła nigdy nie upadnie na
sztorc, to możemy traktować ją jak odcinek o długości
– szerokości deski. Jeżeli przyjmiemy realistyczne założenia, że grubość
igły jest dużo mniejsza od szerokości deski oraz że igła nigdy nie upadnie na
sztorc, to możemy traktować ją jak odcinek o długości
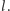
Z powyższej równości wynika bardzo ważny wniosek: wartość
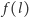 będzie taka sama, gdy zamiast odcinkiem będziemy „rzucać” dowolną łamaną
o długości
będzie taka sama, gdy zamiast odcinkiem będziemy „rzucać” dowolną łamaną
o długości
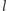 – wystarczy podzielić ją na kawałki prostoliniowe
i użyć równości (1) tyle razy, ile tych kawałków będzie. Stąd dla dowolnego
wielokąta o obwodzie równym
– wystarczy podzielić ją na kawałki prostoliniowe
i użyć równości (1) tyle razy, ile tych kawałków będzie. Stąd dla dowolnego
wielokąta o obwodzie równym
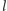 w naszym doświadczeniu
otrzymamy taką samą wartość oczekiwaną liczby przecięć z prostymi
z rodziny
w naszym doświadczeniu
otrzymamy taką samą wartość oczekiwaną liczby przecięć z prostymi
z rodziny
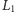 jak dla igły o długości
jak dla igły o długości
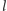 . Tę własność mają
również krzywe o długości
. Tę własność mają
również krzywe o długości
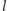 , które możemy podzielić
na małe fragmenty wyglądające prawie jak odcinki. Takie krzywe mogą
być zamknięte (na przykład okrąg spełnia powyższy warunek). Dla
uproszczenia zakładamy, że nie mają samoprzecięć (czyli ósemki
nie uwzględniamy).
, które możemy podzielić
na małe fragmenty wyglądające prawie jak odcinki. Takie krzywe mogą
być zamknięte (na przykład okrąg spełnia powyższy warunek). Dla
uproszczenia zakładamy, że nie mają samoprzecięć (czyli ósemki
nie uwzględniamy).
Zależność (1) jest równaniem funkcyjnym, zwanym równaniem
Cauchy’ego, które przy założeniu ciągłości szukanej funkcji
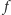 spełniają
tylko funkcje liniowe:
spełniają
tylko funkcje liniowe:
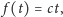 | (2) |
gdzie
 jest stałą. Stałą
jest stałą. Stałą
 można wyznaczyć, zauważając, że
okrąg o promieniu
można wyznaczyć, zauważając, że
okrąg o promieniu
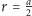 , przy dowolnym ułożeniu na rozważanym
podłożu, zawsze będzie miał dokładnie dwa punkty wspólne z narysowanymi
prostymi. Obwód tego okręgu wynosi
, przy dowolnym ułożeniu na rozważanym
podłożu, zawsze będzie miał dokładnie dwa punkty wspólne z narysowanymi
prostymi. Obwód tego okręgu wynosi
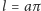 , stąd
, stąd

a więc
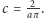
Zauważmy, że odcinek o długości
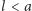 może przeciąć co najwyżej
jedną prostą z rodziny
może przeciąć co najwyżej
jedną prostą z rodziny
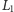 . Zatem w tym przypadku
. Zatem w tym przypadku

gdzie
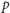 jest szukanym prawdopodobieństwem przecięcia odcinka
i prostej z
jest szukanym prawdopodobieństwem przecięcia odcinka
i prostej z
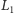 . To daje nam oczekiwany wynik:
. To daje nam oczekiwany wynik:

Stąd właściwie „za darmo” otrzymujemy dowód twierdzenia Barbiera. Zanim
przejdziemy do szczegółów, zwróćmy uwagę, że do wyznaczenia
stałej
 z równości (2) może posłużyć dowolna krzywa
o następującej własności:
z równości (2) może posłużyć dowolna krzywa
o następującej własności:
przy każdym położeniu takiej krzywej na naszym podłożu, podzielonym
prostymi równoległymi z rodziny
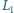 , przecina się ona z prostymi
w dokładnie dwóch punktach.
, przecina się ona z prostymi
w dokładnie dwóch punktach.

Takie krzywe nazywają się krzywymi o stałej szerokości, a najpopularniejszym przykładem takiej krzywej, różnym od okręgu, jest trójkąt Reuleaux. Dodajmy jeszcze, że różnych, parami niepodobnych krzywych, o stałej (i ustalonej) szerokości jest nieskończenie wiele.
Twierdzenie (Barbier, 1860). Figury o stałej szerokości
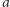 mają
jednakowe obwody równe
mają
jednakowe obwody równe
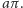
Dowód. Załóżmy, że
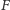 jest figurą o stałej szerokości
jest figurą o stałej szerokości
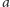 . Figura
. Figura
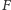 dowolnie
umieszczona na płaszczyźnie z narysowaną rodziną prostych
dowolnie
umieszczona na płaszczyźnie z narysowaną rodziną prostych
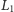 będzie mieć dokładnie dwa punkty wspólne z tymi prostymi. Jeśli
będzie mieć dokładnie dwa punkty wspólne z tymi prostymi. Jeśli
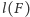 oznacza obwód figury
oznacza obwód figury
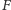 , to bezpośrednio z definicji
funkcji
, to bezpośrednio z definicji
funkcji
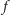 mamy
mamy

Z drugiej strony wiemy już, że
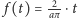 , i dlatego
, i dlatego

Skąd natychmiast otrzymujemy
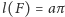 – obwód
figury
– obwód
figury
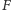 zależy więc jedynie od szerokości
zależy więc jedynie od szerokości
 .
.
Rys. 3 Igła rzucona na płaszczyznę podzieloną rodzinami prostych
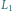 i
i
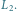
Zajmijmy się teraz nieco innym zadaniem. Dorysujmy na płaszczyźnie
rodzinę prostych równoległych
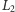 , takich że odległość między
dwiema kolejnymi prostymi z tej rodziny jest równa
, takich że odległość między
dwiema kolejnymi prostymi z tej rodziny jest równa
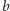 , a rodzina
prostych
, a rodzina
prostych
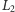 przecina proste
przecina proste
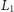 pod danym kątem
pod danym kątem
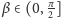 .
W ten sposób otrzymujemy płaszczyznę podzieloną prostymi na przystające
równoległoboki. Obliczmy prawdopodobieństwo tego, że igła przetnie
równocześnie którąkolwiek z prostych rodziny
.
W ten sposób otrzymujemy płaszczyznę podzieloną prostymi na przystające
równoległoboki. Obliczmy prawdopodobieństwo tego, że igła przetnie
równocześnie którąkolwiek z prostych rodziny
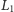 i prostych
rodziny
i prostych
rodziny
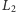 w tej, nieco ogólniejszej, sytuacji. Poniżej przedstawię
rozwiązanie metodą „standardową”, jednak zachęcam do poszukiwania metody
podobnej do powyższej, za pomocą równania funkcyjnego.
w tej, nieco ogólniejszej, sytuacji. Poniżej przedstawię
rozwiązanie metodą „standardową”, jednak zachęcam do poszukiwania metody
podobnej do powyższej, za pomocą równania funkcyjnego.
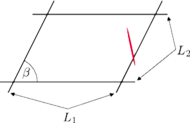
Położenie igły w tym przypadku najlepiej określić, znając kąt
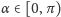 między igłą a prostą rodziny
między igłą a prostą rodziny
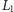 , odległość
, odległość
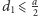 środka igły od
najbliższej prostej z rodziny
środka igły od
najbliższej prostej z rodziny
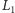 oraz odległość
oraz odległość
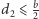 środka
igły od najbliższej prostej rodziny
środka
igły od najbliższej prostej rodziny
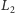 .
.
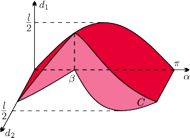
Rys. 4 Zbiór
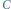 zdarzeń, w których igła przecina prostą z
zdarzeń, w których igła przecina prostą z
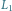 i prostą z
i prostą z
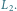
Przestrzenią zdarzeń elementarnych
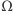 jest zbiór
jest zbiór

Igła przetnie proste, gdy parametry
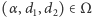 spełniają warunki
spełniają warunki
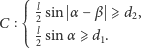 | (3) |
Do obliczenia miary (objętości) powyższego podzbioru
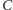 przestrzeni
przestrzeni
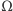 możemy wykorzystać regułę Cavalieriego: żeby
otrzymać objętość
możemy wykorzystać regułę Cavalieriego: żeby
otrzymać objętość
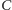 , całkujemy względem
, całkujemy względem
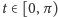 pola
przekrojów
pola
przekrojów
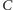 płaszczyznami
płaszczyznami
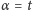 . Łatwo sprawdzić, że każdy
przekrój figury
. Łatwo sprawdzić, że każdy
przekrój figury
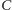 płaszczyzną
płaszczyzną
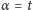 dla
dla
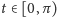 jest
prostokątem o wymiarach
jest
prostokątem o wymiarach
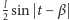 na
na
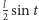 . Otrzymujemy
więc
. Otrzymujemy
więc

Gdy
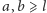 , szukane prawdopodobieństwo wyraża się przez stosunek
objętości obszaru
, szukane prawdopodobieństwo wyraża się przez stosunek
objętości obszaru
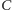 do objętości prostopadłościanu
do objętości prostopadłościanu
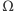 :
:

Można zastanawiać się nad podobnymi zagadnieniami: na przykład, ciekawy wydaje się rzut igłą na płaszczyznę z narysowaną mozaiką złożoną z przystających prostokątów, tworzących „mur z cegieł”. Rozwiązanie tego problemu pozostawiam Czytelnikom.
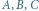 będą wierzchołkami trójkąta równobocznego. Zakreślmy łuk
łączący punkty
będą wierzchołkami trójkąta równobocznego. Zakreślmy łuk
łączący punkty
 i
i
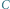 i mający środek w punkcie
i mający środek w punkcie
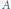 . Analogicznie
zakreślamy łuki od punktu
. Analogicznie
zakreślamy łuki od punktu
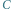 do
do
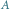 i środku w
i środku w
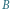 oraz od
oraz od
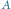 do
do
 o środku w
o środku w
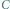 . Łuki te tworzą trójkąt Reuleaux.
. Łuki te tworzą trójkąt Reuleaux.
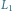 i
i
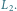
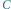 zdarzeń, w których igła przecina prostą z
zdarzeń, w których igła przecina prostą z
 i prostą z
i prostą z