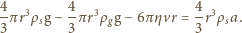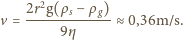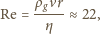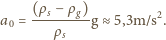Zadania z fizyki - XI 2020»Zadanie 1011
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z fizyki - XI 2020
- Publikacja w Delcie: listopad 2020
- Publikacja elektroniczna: 1 listopada 2020
Siła nośna 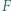 utrzymująca ptaka podczas lotu wynosi:
utrzymująca ptaka podczas lotu wynosi:
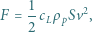 |
gdzie 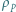 jest gęstością powietrza,
jest gęstością powietrza,  prędkością lotu (względem powietrza),
prędkością lotu (względem powietrza), 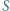 powierzchnią skrzydeł, a
powierzchnią skrzydeł, a 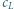 współczynnikiem związanym z kształtem lecącego ptaka. Opierając się na tym, że siła oporu powietrza jest proporcjonalna do
współczynnikiem związanym z kształtem lecącego ptaka. Opierając się na tym, że siła oporu powietrza jest proporcjonalna do 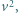 oszacuj, jak optymalna predkość poziomego lotu zależy od masy
oszacuj, jak optymalna predkość poziomego lotu zależy od masy 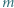 ptaka.
ptaka.
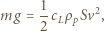
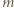
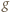
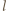 - np. rozpiętość skrzydeł. Zachodzi wówczas skalowanie:
- np. rozpiętość skrzydeł. Zachodzi wówczas skalowanie: 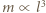
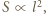
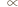 " oznacza proporcjonalność. Podstawienie tych relacji do podanego wyżej równania na siłę nośną prowadzi do oszacowania:
" oznacza proporcjonalność. Podstawienie tych relacji do podanego wyżej równania na siłę nośną prowadzi do oszacowania: 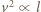
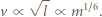
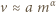

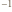
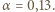
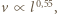
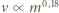 (Knut Schmidt-Nielsen, Dlaczego tak ważne są rozmiary zwierząt, Wydawnictwo Naukowe PWN, Warszawa 1994).
(Knut Schmidt-Nielsen, Dlaczego tak ważne są rozmiary zwierząt, Wydawnictwo Naukowe PWN, Warszawa 1994).
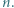 Czy w głębokiej wodzie układ będzie pływał, czy utonie? Należy przyjąć, że masy pręta i lekkiej kulki są zaniedbywalne.
Czy w głębokiej wodzie układ będzie pływał, czy utonie? Należy przyjąć, że masy pręta i lekkiej kulki są zaniedbywalne.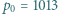 hPa, ale panuje tam przeważnie spokojna, bezwietrzna pogoda. Na zewnątrz tego obszaru, w promieniu do kilkuset kilometrów, wieją bardzo gwałtowne wiatry. Oko cyklonu Wilma w październiku 2005 roku miało promień około
hPa, ale panuje tam przeważnie spokojna, bezwietrzna pogoda. Na zewnątrz tego obszaru, w promieniu do kilkuset kilometrów, wieją bardzo gwałtowne wiatry. Oko cyklonu Wilma w październiku 2005 roku miało promień około 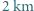 , panowało w nim ciśnienie 882 hPa, a silne wiatry występowały do
, panowało w nim ciśnienie 882 hPa, a silne wiatry występowały do 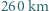 od centrum. Oszacuj prędkość wiatru wokół oka tego cyklonu. Przyjmij, że gęstość powietrza
od centrum. Oszacuj prędkość wiatru wokół oka tego cyklonu. Przyjmij, że gęstość powietrza 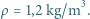
 i
i 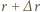 od oka cyklonu. Rozważmy fragment strugi wiatru o szerokości
od oka cyklonu. Rozważmy fragment strugi wiatru o szerokości 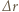 i powierzchni
i powierzchni 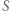 w kierunku prostopadłym do promienia. Równowaga działających sił prowadzi do równania:
w kierunku prostopadłym do promienia. Równowaga działających sił prowadzi do równania: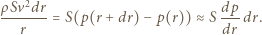
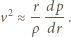
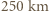 , wynosi 1010 hPa. Według naszego wzoru prędkość wynosi zero w centrum i rośnie z
, wynosi 1010 hPa. Według naszego wzoru prędkość wynosi zero w centrum i rośnie z 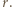 Z dala od centrum zmiany ciśnienia maleją i na krańcu cyklonu pochodna ciśnienia wynosi zero. Przyjmijmy, że maksymalna prędkość osiągana jest w odległości
Z dala od centrum zmiany ciśnienia maleją i na krańcu cyklonu pochodna ciśnienia wynosi zero. Przyjmijmy, że maksymalna prędkość osiągana jest w odległości 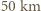 od centrum, i do obliczeń weźmy średnią wartość pochodnej
od centrum, i do obliczeń weźmy średnią wartość pochodnej 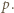 Otrzymujemy:
Otrzymujemy: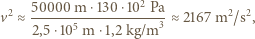
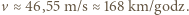 Maksymalny zarejestrowany poryw wiatru cyklonu Wilma osiągnął
Maksymalny zarejestrowany poryw wiatru cyklonu Wilma osiągnął 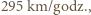 ale przez większość blisko dwutygodniowego "życia" tego cyklonu maksymalna prędkość wiatru wynosiła od 175 do
ale przez większość blisko dwutygodniowego "życia" tego cyklonu maksymalna prędkość wiatru wynosiła od 175 do 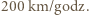
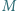 i wysokości
i wysokości 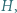 którego pole podstawy wynosi
którego pole podstawy wynosi 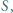 wypełniony jest gazem doskonałym i pływa w wodzie. W wyniku utraty hermetyczności w dolnej części cylindra, jego głębokość zanurzenia zwiększyła się o
wypełniony jest gazem doskonałym i pływa w wodzie. W wyniku utraty hermetyczności w dolnej części cylindra, jego głębokość zanurzenia zwiększyła się o 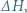 Jakie było ciśnienie początkowe gazu w cylindrze? Ciśnienie atmosferyczne wynosi
Jakie było ciśnienie początkowe gazu w cylindrze? Ciśnienie atmosferyczne wynosi 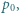 temperatura nie zmienia się.
temperatura nie zmienia się.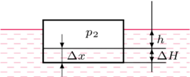
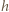 początkową głębokość zanurzenia cylindra, a przez
początkową głębokość zanurzenia cylindra, a przez 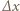 wysokość słupa wody, która wciekła do naczynia po utracie hermetyczności. Zgodnie z prawem Archimedesa
wysokość słupa wody, która wciekła do naczynia po utracie hermetyczności. Zgodnie z prawem Archimedesa 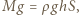 gdzie
gdzie 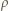 jest gęstością wody. Stąd
jest gęstością wody. Stąd 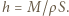 W stanie końcowym:
W stanie końcowym: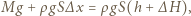
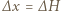 (rysunek obok). Warunek równowagi ciśnień na głębokości
(rysunek obok). Warunek równowagi ciśnień na głębokości 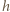 ma postać:
ma postać: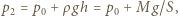
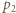 jest ciśnieniem gazu w naczyniu w stanie końcowym. Oznaczając szukane ciśnienie początkowe przez
jest ciśnieniem gazu w naczyniu w stanie końcowym. Oznaczając szukane ciśnienie początkowe przez 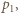 z prawa przemiany izotermicznej otrzymujemy:
z prawa przemiany izotermicznej otrzymujemy: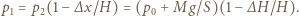
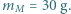 Ile wynosi rzeczywista masa
Ile wynosi rzeczywista masa 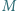 figurki? Gęstość hebanu
figurki? Gęstość hebanu 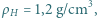 gęstość mosiądzu
gęstość mosiądzu 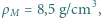 a powietrza
a powietrza 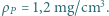
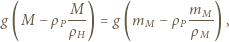
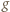 oznacza przyspieszenie ziemskie. Otrzymujemy stąd:
oznacza przyspieszenie ziemskie. Otrzymujemy stąd: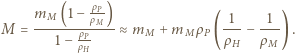
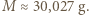
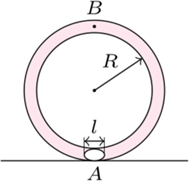
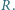 Pierścień napełniono wodą, z wyjątkiem niewielkiego odcinka o długości
Pierścień napełniono wodą, z wyjątkiem niewielkiego odcinka o długości 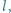 gdzie znajduje się kropla oleju, i postawiono pionowo. W chwili początkowej (rysunek) kropla zaczyna wypływać z punktu
gdzie znajduje się kropla oleju, i postawiono pionowo. W chwili początkowej (rysunek) kropla zaczyna wypływać z punktu 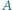 w kierunku punktu
w kierunku punktu 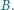 Znaleźć jej prędkość, gdy mija punkt
Znaleźć jej prędkość, gdy mija punkt 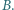 Gęstość wody wynosi
Gęstość wody wynosi 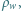 oleju
oleju 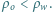 Długość kropli oleju jest dużo mniejsza od promienia pierścienia. Tarcie zaniedbujemy. Nie zachodzi przesączanie przez olejowy "korek".
Długość kropli oleju jest dużo mniejsza od promienia pierścienia. Tarcie zaniedbujemy. Nie zachodzi przesączanie przez olejowy "korek". szukaną prędkość kropli w chwili, gdy przechodzi ona przez punkt
szukaną prędkość kropli w chwili, gdy przechodzi ona przez punkt 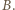 W czasie, gdy kropla oleju przemieszcza się z punktu
W czasie, gdy kropla oleju przemieszcza się z punktu 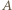 do
do 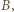 porcja wody o tej samej objętości przemieszcza się z
porcja wody o tej samej objętości przemieszcza się z 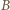 do
do 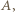 czyli obniża się o
czyli obniża się o 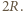 Energia potencjalna pozostałej masy wody nie zmienia się. Zasada zachowania energii ma postać
Energia potencjalna pozostałej masy wody nie zmienia się. Zasada zachowania energii ma postać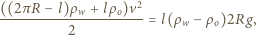
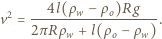
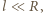 to w przybliżeniu
to w przybliżeniu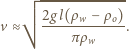
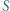 wlano wodę, w której pływa kawałek lodu z kulką ołowianą wewnątrz. Objętość lodu razem z kulką jest równa
wlano wodę, w której pływa kawałek lodu z kulką ołowianą wewnątrz. Objętość lodu razem z kulką jest równa 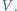 Nad wodę wystaje
Nad wodę wystaje 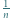 część tej objętości. Jak zmieni się poziom wody w naczyniu po stopieniu lodu? Gęstości wody, lodu i ołowiu wynoszą odpowiednio
część tej objętości. Jak zmieni się poziom wody w naczyniu po stopieniu lodu? Gęstości wody, lodu i ołowiu wynoszą odpowiednio 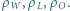
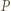 na dno naczynia nie zmienia się po stopieniu wody, bo nie zmienia się ciężar zawartości naczynia, a ścianki cylindra są pionowe:
na dno naczynia nie zmienia się po stopieniu wody, bo nie zmienia się ciężar zawartości naczynia, a ścianki cylindra są pionowe: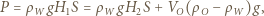
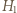 i
i 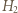 oznaczają wysokości słupa wody w naczyniu przed i po stopieniu lodu,
oznaczają wysokości słupa wody w naczyniu przed i po stopieniu lodu, 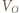 jest objętością ołowiu. Różnica wysokości poziomów wody wynosi
jest objętością ołowiu. Różnica wysokości poziomów wody wynosi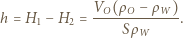
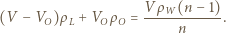
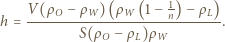
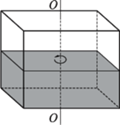
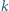 -ta część powierzchni dna. Jak zmieniła się w wyniku tego siła parcia na dno i wąskie ścianki boczne (w porównaniu z przypadkiem nieruchomego naczynia)? Ciecz nie wylewa się z naczynia. Napięcie powierzchniowe można zaniedbać.
-ta część powierzchni dna. Jak zmieniła się w wyniku tego siła parcia na dno i wąskie ścianki boczne (w porównaniu z przypadkiem nieruchomego naczynia)? Ciecz nie wylewa się z naczynia. Napięcie powierzchniowe można zaniedbać.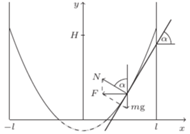
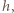 a rozmiary podstawy naczynia przez
a rozmiary podstawy naczynia przez 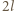 i
i 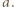 Zgodnie z treścią zadania
Zgodnie z treścią zadania 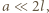 możemy więc przyjąć, że powierzchnia cieczy w obracającym się naczyniu ma kształt jak na rysunku.
możemy więc przyjąć, że powierzchnia cieczy w obracającym się naczyniu ma kształt jak na rysunku.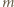 na jej powierzchni w obracającym się naczyniu. Działa na niego siła ciężkości
na jej powierzchni w obracającym się naczyniu. Działa na niego siła ciężkości 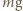 i siła reakcji
i siła reakcji 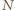 ze strony pozostałej cieczy, prostopadła do jej powierzchni. Wypadkowa tych dwóch sił jest siłą dośrodkową o wartości
ze strony pozostałej cieczy, prostopadła do jej powierzchni. Wypadkowa tych dwóch sił jest siłą dośrodkową o wartości 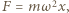 gdzie
gdzie 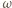 jest prędkością kątową, a
jest prędkością kątową, a 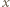 odległością elementu cieczy od osi obrotu. Styczna do powierzchni cieczy w badanym punkcie nachylona jest do poziomu pod kątem
odległością elementu cieczy od osi obrotu. Styczna do powierzchni cieczy w badanym punkcie nachylona jest do poziomu pod kątem  i spełnione są związki:
i spełnione są związki: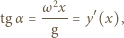
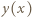 opisuje kształt powierzchni cieczy. Stąd
opisuje kształt powierzchni cieczy. Stąd 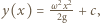 a stałą
a stałą  możemy wyznaczyć z warunków brzegowych. Gdy
możemy wyznaczyć z warunków brzegowych. Gdy 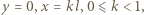 zatem
zatem 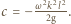 Ponieważ ciecz jest nieściśliwa i jej objętość stała, możemy wyznaczyć prędkość kątową obracającego się naczynia, przyrównując objętość cieczy w połówce naczynia spoczywającego i obracającego się:
Ponieważ ciecz jest nieściśliwa i jej objętość stała, możemy wyznaczyć prędkość kątową obracającego się naczynia, przyrównując objętość cieczy w połówce naczynia spoczywającego i obracającego się: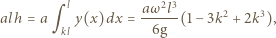
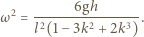
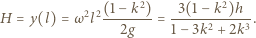
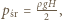 gdzie
gdzie 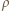 jest gęstością cieczy. Szukany stosunek parć na ściankę boczną w obracającym się i nieruchomym naczyniu równy jest
jest gęstością cieczy. Szukany stosunek parć na ściankę boczną w obracającym się i nieruchomym naczyniu równy jest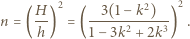
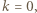 otrzymujemy
otrzymujemy 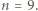
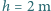 wydzielają się pęcherzyki gazu o średnicy
wydzielają się pęcherzyki gazu o średnicy 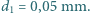 Jaka będzie średnica
Jaka będzie średnica 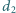 tych pęcherzyków, gdy osiągną one powierzchnię wody? Napięcie powierzchniowe wody wynosi
tych pęcherzyków, gdy osiągną one powierzchnię wody? Napięcie powierzchniowe wody wynosi 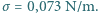 Dla ciśnienia atmosferycznego przyjąć wartość
Dla ciśnienia atmosferycznego przyjąć wartość 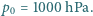
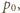 ciśnienie słupa wody
ciśnienie słupa wody 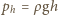 (
( 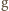 - przyspieszenie ziemskie,
- przyspieszenie ziemskie, 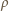 - gęstość wody) i ciśnienie wynikające z napięcia powierzchniowego
- gęstość wody) i ciśnienie wynikające z napięcia powierzchniowego 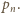 Przy powierzchni wody na ciśnienie w pęcherzyku składa się ciśnienie atmosferyczne
Przy powierzchni wody na ciśnienie w pęcherzyku składa się ciśnienie atmosferyczne 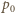 i ciśnienie wynikające z napięcia powierzchniowego
i ciśnienie wynikające z napięcia powierzchniowego 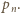
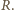 Jeżeli powiększymy jego promień o
Jeżeli powiększymy jego promień o 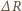 to powierzchnia wzrośnie o
to powierzchnia wzrośnie o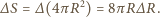
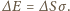 Powiększenie promienia pęcherzyka jest skutkiem wykonania pracy
Powiększenie promienia pęcherzyka jest skutkiem wykonania pracy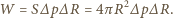
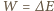 otrzymujemy na dodatkowe ciśnienie wyrażenie
otrzymujemy na dodatkowe ciśnienie wyrażenie 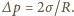
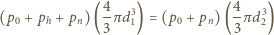
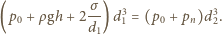
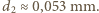 Zauważmy, że wkład od napięcia powierzchniowego jest znacznie mniejszy od ciśnienia atmosferycznego i hydrostatycznego i może być pominięty.
Zauważmy, że wkład od napięcia powierzchniowego jest znacznie mniejszy od ciśnienia atmosferycznego i hydrostatycznego i może być pominięty.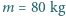 nabrał pełno powietrza do płuc
nabrał pełno powietrza do płuc 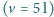 i wskoczył do wody. Z jakiej maksymalnej głębokości
i wskoczył do wody. Z jakiej maksymalnej głębokości 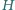 nurek może wypłynąć, nie wykonując żadnych ruchów? Objętość ciała nurka to
nurek może wypłynąć, nie wykonując żadnych ruchów? Objętość ciała nurka to 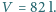
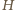 średnia gęstość nurka powinna być równa gęstości wody, a więc jego objętość powinna być równa
średnia gęstość nurka powinna być równa gęstości wody, a więc jego objętość powinna być równa 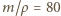 l, gdzie
l, gdzie 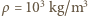 to gęstość wody. Zmniejszenie objętości ciała o wielkość
to gęstość wody. Zmniejszenie objętości ciała o wielkość 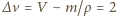 nastąpi - praktycznie biorąc - tylko w efekcie sprężenia powietrza w płucach, którego objętość zmaleje do
nastąpi - praktycznie biorąc - tylko w efekcie sprężenia powietrza w płucach, którego objętość zmaleje do 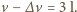 Przyjmując, że sprężenie następuje w stałej temperaturze, można zastosować prawo Boyle'a-Mariotte'a:
Przyjmując, że sprężenie następuje w stałej temperaturze, można zastosować prawo Boyle'a-Mariotte'a: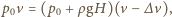
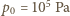 to ciśnienie atmosferyczne. Stąd otrzymujemy, że nurek może wypłynąć, nie wykonując żadnych ruchów, z głębokości nieco mniejszej od
to ciśnienie atmosferyczne. Stąd otrzymujemy, że nurek może wypłynąć, nie wykonując żadnych ruchów, z głębokości nieco mniejszej od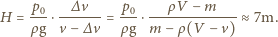
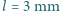 , a średnica tułowia jest równa szerokości skrzydła
, a średnica tułowia jest równa szerokości skrzydła 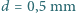 . Gęstość powietrza to
. Gęstość powietrza to 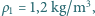 a średnia gęstość komara
a średnia gęstość komara 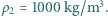
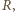 działającą na skrzydło, możemy oszacować, posługując się analizą wymiarową, przyjmując, że siła ta zależy od gęstości powietrza, prędkości jego strumienia oraz pola powierzchni prostopadłego do niego przekroju poprzecznego:
działającą na skrzydło, możemy oszacować, posługując się analizą wymiarową, przyjmując, że siła ta zależy od gęstości powietrza, prędkości jego strumienia oraz pola powierzchni prostopadłego do niego przekroju poprzecznego: 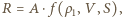 a współczynnik
a współczynnik 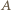 dla zakresu prędkości, z jakim mamy do czynienia, to około 1/2.
dla zakresu prędkości, z jakim mamy do czynienia, to około 1/2.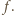 Założymy, że amplituda machnięć jest rzędu długości skrzydła
Założymy, że amplituda machnięć jest rzędu długości skrzydła 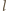 i że skrzydła opuszczają się płasko, a podnoszą się krawędzią tak, że opór powietrza przy podnoszeniu można pominąć. Średnia prędkość powietrza odrzucanego skrzydłami w dół wynosi
i że skrzydła opuszczają się płasko, a podnoszą się krawędzią tak, że opór powietrza przy podnoszeniu można pominąć. Średnia prędkość powietrza odrzucanego skrzydłami w dół wynosi 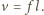 Posługując się analizą wymiarową, znajdujemy, że
Posługując się analizą wymiarową, znajdujemy, że 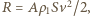 gdzie
gdzie 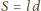 to powierzchnia skrzydła (współczynnik
to powierzchnia skrzydła (współczynnik 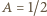 z warunków zadania). Siła unosząca
z warunków zadania). Siła unosząca 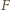 jest równa średniej czasowej siły oporu działającej na skrzydło, pomnożonej przez liczbę skrzydeł i podzielonej przez dwa, ponieważ opór powietrza działa na skrzydło tylko przy jego ruchu w dół. Stąd
jest równa średniej czasowej siły oporu działającej na skrzydło, pomnożonej przez liczbę skrzydeł i podzielonej przez dwa, ponieważ opór powietrza działa na skrzydło tylko przy jego ruchu w dół. Stąd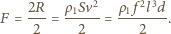
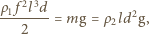
 to masa komara, g - przyspieszenie ziemskie. Ostatecznie
to masa komara, g - przyspieszenie ziemskie. Ostatecznie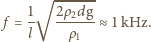
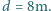 Czy uda mu się wznieść, jeżeli jego masa wraz z masą helikoptera wynosi
Czy uda mu się wznieść, jeżeli jego masa wraz z masą helikoptera wynosi 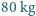 ? Przyjąć, że kolarz-amator przy długotrwałym wysiłku rozwija moc około 150 W. Masa cząsteczkowa powietrza to
? Przyjąć, że kolarz-amator przy długotrwałym wysiłku rozwija moc około 150 W. Masa cząsteczkowa powietrza to 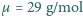 .
.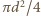 z prędkością
z prędkością 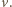 Jeżeli gęstość powietrza wynosi
Jeżeli gęstość powietrza wynosi 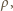 to w czasie
to w czasie 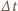 wirnik nadaje powietrzu o masie
wirnik nadaje powietrzu o masie 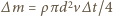 pęd
pęd 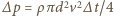 i energię kinetyczną
i energię kinetyczną 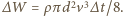 Aby helikopter się wzniósł, wirnik musi wytworzyć siłę ciągu równą ciężarowi helikoptera z pilotem:
Aby helikopter się wzniósł, wirnik musi wytworzyć siłę ciągu równą ciężarowi helikoptera z pilotem: 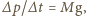 a potrzebna do tego moc wynosi
a potrzebna do tego moc wynosi 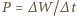 (g - przyspieszenie ziemskie). Korzystając z tego, że w warunkach normalnych objętość jednego mola gazu to
(g - przyspieszenie ziemskie). Korzystając z tego, że w warunkach normalnych objętość jednego mola gazu to 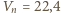 litra, znajdujemy, że gęstość powietrza wynosi
litra, znajdujemy, że gęstość powietrza wynosi 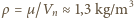 i otrzymujemy
i otrzymujemy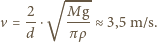
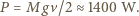
 rośnie z jej średnicą. Obserwacje wskazują, że duże krople osiągają prędkość około 10 m/s. Oszacuj, jakie średnie ciśnienie
rośnie z jej średnicą. Obserwacje wskazują, że duże krople osiągają prędkość około 10 m/s. Oszacuj, jakie średnie ciśnienie 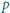 wywiera na poziomy dach bardzo silny deszcz o intensywności
wywiera na poziomy dach bardzo silny deszcz o intensywności 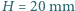 na godzinę (zakładamy, że woda natychmiast spływa rynnami). Przyjmij, że gęstość wody to
na godzinę (zakładamy, że woda natychmiast spływa rynnami). Przyjmij, że gęstość wody to 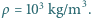
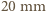 na godzinę oznacza, że na
na godzinę oznacza, że na 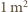 powierzchni spada w ciągu godziny
powierzchni spada w ciągu godziny 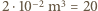 l wody. Uderzenia kropel deszczu o dach są zderzeniami niesprężystymi i przekazywany przez nie dachowi pęd wynosi
l wody. Uderzenia kropel deszczu o dach są zderzeniami niesprężystymi i przekazywany przez nie dachowi pęd wynosi 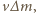 gdzie
gdzie 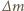 oznacza masę wody. Ciśnienie równa się sile działającej na jednostkę powierzchni. Mamy więc
oznacza masę wody. Ciśnienie równa się sile działającej na jednostkę powierzchni. Mamy więc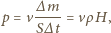
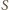 oznacza powierzchnię dachu, a
oznacza powierzchnię dachu, a 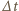 czas, w którym na dach spadła masa wody równa
czas, w którym na dach spadła masa wody równa 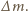 Otrzymujemy
Otrzymujemy 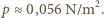 Jest to wartość bardzo mała - gdyby woda nie spływała z dachu, to już po pierwszej minucie opadu wywierałaby ciśnienie
Jest to wartość bardzo mała - gdyby woda nie spływała z dachu, to już po pierwszej minucie opadu wywierałaby ciśnienie 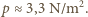
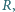 a gęstość wody wynosi
a gęstość wody wynosi 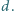
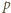 wywierane na stół w momencie, gdy woda zaczyna wyciekać dołem, wynosi
wywierane na stół w momencie, gdy woda zaczyna wyciekać dołem, wynosi 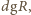 a siła parcia na stół wynosi
a siła parcia na stół wynosi 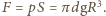 Siła ta jest zarazem równa wspólnej masie dzwonu i wody
Siła ta jest zarazem równa wspólnej masie dzwonu i wody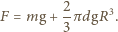
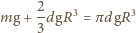
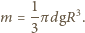
 fali od jej długości
fali od jej długości 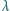 dla fal na powierzchni głębokiego zbiornika nieściśliwej cieczy - to znaczy gdy głębokość zbiornika
dla fal na powierzchni głębokiego zbiornika nieściśliwej cieczy - to znaczy gdy głębokość zbiornika 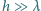 - w przypadku, gdy źródłem sił przywracających płaskość powierzchni jest:
- w przypadku, gdy źródłem sił przywracających płaskość powierzchni jest: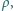 współczynnik napięcia powierzchniowego ciecz-powietrze
współczynnik napięcia powierzchniowego ciecz-powietrze 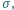 a przyspieszenie siły ciężkości wynosi
a przyspieszenie siły ciężkości wynosi 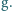
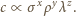
 jest
jest 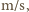 napięcia powierzchniowego
napięcia powierzchniowego 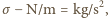 gęstości
gęstości 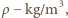 a długości fali
a długości fali 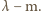 Po porównaniu wymiarów lewej i prawej strony otrzymujemy:
Po porównaniu wymiarów lewej i prawej strony otrzymujemy: 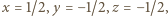 czyli:
czyli: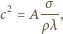
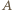 jest pewną bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal kapilarnych prowadzi do wartości
jest pewną bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal kapilarnych prowadzi do wartości 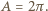 Znaleziona zależność poprawnie opisuje zachowanie bardzo krótkich fal
Znaleziona zależność poprawnie opisuje zachowanie bardzo krótkich fal 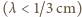 na powierzchni wody.
na powierzchni wody.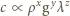
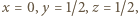 czyli:
czyli: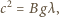
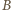 jest bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal grawitacyjnych prowadzi do
jest bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal grawitacyjnych prowadzi do 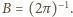 Znaleziona zależność poprawnie opisuje fale na wodzie, gdy
Znaleziona zależność poprawnie opisuje fale na wodzie, gdy 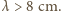
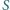 jest dużo mniejsza od powierzchni dna naczynia. W naczyniu znajduje się ciecz o gęstości
jest dużo mniejsza od powierzchni dna naczynia. W naczyniu znajduje się ciecz o gęstości 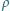 i stałej dielektrycznej
i stałej dielektrycznej  Wysokość słupa cieczy jest dużo mniejsza od rozmiarów liniowych płytki. O ile podniesie się ciecz nad płytką, gdy na płytkę wprowadzony zostanie ładunek
Wysokość słupa cieczy jest dużo mniejsza od rozmiarów liniowych płytki. O ile podniesie się ciecz nad płytką, gdy na płytkę wprowadzony zostanie ładunek 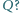
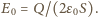 Na powierzchniach warstwy cieczy nad płytką powstają ładunki indukowane
Na powierzchniach warstwy cieczy nad płytką powstają ładunki indukowane 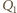 oraz
oraz 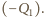 Wypadkowe pole nad płytką możemy zapisać na dwa sposoby
Wypadkowe pole nad płytką możemy zapisać na dwa sposoby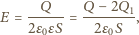
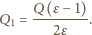
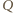 na płytce i ładunek indukowany
na płytce i ładunek indukowany 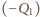 na dolnej powierzchni warstwy cieczy dielektrycznej odpychają ładunek indukowany
na dolnej powierzchni warstwy cieczy dielektrycznej odpychają ładunek indukowany 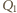 na górnej powierzchni cieczy, dana jest wzorem
na górnej powierzchni cieczy, dana jest wzorem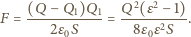
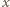 i jest równoważona dodatkową siłą ciężkości o wartości
i jest równoważona dodatkową siłą ciężkości o wartości 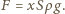 Szukana wysokość, na jaką podniesie się ciecz, wynosi
Szukana wysokość, na jaką podniesie się ciecz, wynosi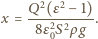
 od jej długości
od jej długości 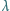 dla fal na powierzchni głębokiego zbiornika cieczy - tzn. gdy głębokość zbiornika
dla fal na powierzchni głębokiego zbiornika cieczy - tzn. gdy głębokość zbiornika 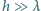 w przypadku, gdy źródłem sił przywracających płaskość powierzchni jest:
w przypadku, gdy źródłem sił przywracających płaskość powierzchni jest: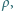 współczynnik napięcia powierzchniowego ciecz-powietrze
współczynnik napięcia powierzchniowego ciecz-powietrze 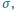 a przyspieszenie siły ciężkości wynosi
a przyspieszenie siły ciężkości wynosi 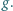
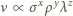
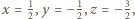 czyli:
czyli: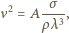
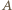 jest pewną bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal kapilarnych prowadzi do wartości
jest pewną bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal kapilarnych prowadzi do wartości 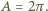 Znaleziona zależność poprawnie opisuje zachowanie bardzo krótkich fal
Znaleziona zależność poprawnie opisuje zachowanie bardzo krótkich fal 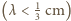 na powierzchni wody.
na powierzchni wody.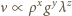
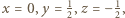 czyli:
czyli: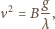
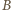 jest bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal grawitacyjnych prowadzi do
jest bezwymiarową stałą - ścisłe rozwiązanie zagadnienia dla fal grawitacyjnych prowadzi do 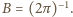 Znaleziona zależność poprawnie opisuje fale na wodzie, gdy
Znaleziona zależność poprawnie opisuje fale na wodzie, gdy 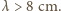
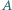 przeciw siłom napięcia powierzchniowego należy wykonać, aby nadmuchać bańkę mydlaną o promieniu
przeciw siłom napięcia powierzchniowego należy wykonać, aby nadmuchać bańkę mydlaną o promieniu 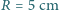 ? Współczynnik napięcia powierzchniowego
? Współczynnik napięcia powierzchniowego 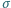 dla wody z mydłem wynosi około
dla wody z mydłem wynosi około 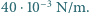
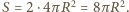 Biorąc pod uwagę, że przed powstaniem bańki powierzchnia wody mydlanej, z której bańka powstała, była zaniedbywalnie mała, można przyjąć, że powyższy wzór wyraża zmianę (przyrost) powierzchni wody mydlanej. Powiększenie powierzchni cieczy o
Biorąc pod uwagę, że przed powstaniem bańki powierzchnia wody mydlanej, z której bańka powstała, była zaniedbywalnie mała, można przyjąć, że powyższy wzór wyraża zmianę (przyrost) powierzchni wody mydlanej. Powiększenie powierzchni cieczy o 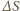 wiąże się ze wzrostem energii powierzchniowej o
wiąże się ze wzrostem energii powierzchniowej o 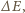 zgodnie ze wzorem
zgodnie ze wzorem 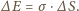 Wykonywana przy nadmuchiwaniu bańki praca jest zużywana właśnie na powiększenie energii powierzchniowej, czyli
Wykonywana przy nadmuchiwaniu bańki praca jest zużywana właśnie na powiększenie energii powierzchniowej, czyli 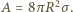 Podstawiając wartości, otrzymujemy
Podstawiając wartości, otrzymujemy 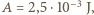 czyli
czyli 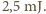
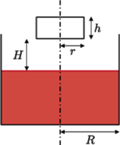
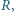 częściowo wypełnionego cieczą, wpada klocek w kształcie walca o promieniu
częściowo wypełnionego cieczą, wpada klocek w kształcie walca o promieniu  i wysokości
i wysokości 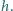 W chwili początkowej odległość dolnej powierzchni klocka od powierzchni cieczy wynosi
W chwili początkowej odległość dolnej powierzchni klocka od powierzchni cieczy wynosi 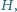 a jego prędkość jest równa zeru. Ile ciepła wydzieli się do chwili, gdy ustanie ruch klocka i cieczy? Gęstość klocka wynosi
a jego prędkość jest równa zeru. Ile ciepła wydzieli się do chwili, gdy ustanie ruch klocka i cieczy? Gęstość klocka wynosi 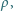 gęstość cieczy
gęstość cieczy 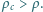
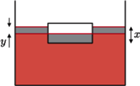
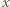 głębokość zanurzenia klocka po ustaleniu się równowagi, a przez
głębokość zanurzenia klocka po ustaleniu się równowagi, a przez 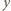 wzrost poziomu cieczy w naczyniu. Zgodnie z prawem Archimedesa
wzrost poziomu cieczy w naczyniu. Zgodnie z prawem Archimedesa 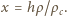 Z rysunku widać, że zachodzi związek
Z rysunku widać, że zachodzi związek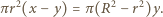
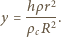
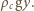 Zatem zachodzi związek
Zatem zachodzi związek 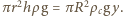 Po ustaleniu się równowagi energia potencjalna klocka zmalała o wielkość
Po ustaleniu się równowagi energia potencjalna klocka zmalała o wielkość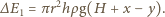
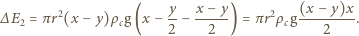
![1 hρ r2 Q = ∆E1 −∆ E2 =-πr2ρgh [H+ ---(1 − -2)] . 2 2ρc R](/math/temat/fizyka/plyny/zadania/2015/12/30/zf-k44-611/10x-347e3330a084016bdaec8cb9d22de6f1b7c693d4-dm-66,57,43-FF,FF,FF.gif)
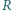 obraca się ruchem jednostajnym w płaszczyźnie pionowej wokół nieruchomej osi. Prędkość punktów na obwodzie koła wynosi
obraca się ruchem jednostajnym w płaszczyźnie pionowej wokół nieruchomej osi. Prędkość punktów na obwodzie koła wynosi 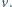 Znaleźć granicę obszaru suchego.
Znaleźć granicę obszaru suchego.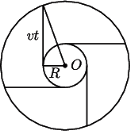


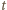 znajdowały się na okręgu o środku w punkcie
znajdowały się na okręgu o środku w punkcie 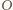 (
(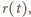 przy czym
przy czym 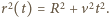 W polu ciężkości środek okręgu obniża się i w czasie
W polu ciężkości środek okręgu obniża się i w czasie 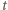 przebywa drogę
przebywa drogę 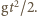 Granica obszaru suchego jest obwiednią okręgów, na których znajdują się w kolejnych momentach krople, które oderwały się jednocześnie od obręczy. Przyjmijmy, że początek układu współrzędnych znajduje się w środku obracającego się koła. Równanie "spadającego" okręgu ma w chwili
Granica obszaru suchego jest obwiednią okręgów, na których znajdują się w kolejnych momentach krople, które oderwały się jednocześnie od obręczy. Przyjmijmy, że początek układu współrzędnych znajduje się w środku obracającego się koła. Równanie "spadającego" okręgu ma w chwili 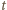 postać:
postać: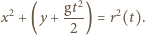
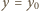 (
(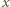 odpowiadającej jednemu z okręgów przecinających tę prostą:
odpowiadającej jednemu z okręgów przecinających tę prostą: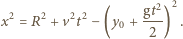
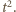 Jego wartość maksymalna
Jego wartość maksymalna 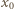 spełnia równanie:
spełnia równanie: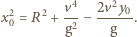
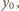 otrzymujemy równanie krzywej opisującej granicę "suchego" obszaru:
otrzymujemy równanie krzywej opisującej granicę "suchego" obszaru: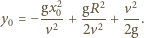
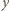 na wysokości
na wysokości 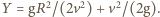 Gdy
Gdy 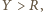 czyli spełniony jest warunek
czyli spełniony jest warunek 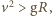 poszukiwana krzywa leży na zewnątrz obręczy. W przeciwnym przypadku granica "mokrego" obszaru przebiega w górnej części po obręczy (
poszukiwana krzywa leży na zewnątrz obręczy. W przeciwnym przypadku granica "mokrego" obszaru przebiega w górnej części po obręczy (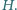 Pchnięcie naczynia w kierunku równoległym do jego ściany bocznej o długości
Pchnięcie naczynia w kierunku równoległym do jego ściany bocznej o długości 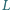 wywołuje kołysanie wody, której powierzchnia pozostaje niemal doskonale płaska. Ile, w przybliżeniu, wynosi okres takich drgań? Zakładamy, że podczas drgań zmiany położenia powierzchni wody są małe w porównaniu z
wywołuje kołysanie wody, której powierzchnia pozostaje niemal doskonale płaska. Ile, w przybliżeniu, wynosi okres takich drgań? Zakładamy, że podczas drgań zmiany położenia powierzchni wody są małe w porównaniu z 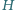 i
i 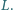 Przyspieszenie ziemskie wynosi
Przyspieszenie ziemskie wynosi 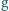 .
.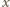 równoległej do
równoległej do 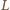 oraz osi
oraz osi 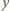 skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny
skierowanej pionowo w górę. Środek ciężkości wody przez cały czas ruchu pozostaje w jednakowej odległości od pionowych ścian akwarium równoległych do płaszczyzny 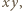 a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej
a okres badanych drgań nie zależy od szerokości naczynia. Podczas drgań, gdy na bocznej ściance o współrzędnej 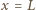 woda podnosi się na wysokość
woda podnosi się na wysokość 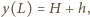 to na ściance
to na ściance 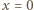 opada do
opada do 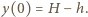 Środek ciężkości wody przesuwa się wówczas z położenia równowagi
Środek ciężkości wody przesuwa się wówczas z położenia równowagi 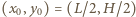 w położenie:
w położenie: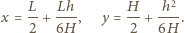
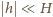 oraz
oraz 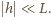 Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego
Wyprowadzając powyższe wyrażenia, skorzystaliśmy z faktu, że dla każdego 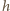 rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną
rozkład wody w naczyniu możemy otrzymać, dodając do rozkładu równowagowego wodę wypełniającą prostopadłościan o podstawie trójkąta prostokątnego z poziomą przyprostokątną 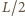 i pionową
i pionową 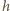 - po stronie
- po stronie 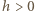 i odejmując taki sam prostopadłościan po stronie
i odejmując taki sam prostopadłościan po stronie 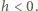 Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc:
Pamiętamy też, że środek ciężkości jednorodnego trójkąta leży na przecięciu środkowych jego boków - dla trójkąta prostokątnego rzuty prostokątne środka ciężkości wypadają w 1/3 odpowiednich przyprostokątnych, licząc od wierzchołka kąta prostego. Kwadrat prędkości ruchu środka masy wynosi więc: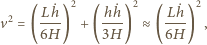
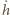 oznacza pochodną
oznacza pochodną 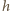 względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa
względem czasu. Jako kolejne przybliżenie przyjmijmy, że cała masa 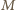 wody porusza się z tą sama prędkością
wody porusza się z tą sama prędkością 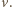 Wówczas zmiany całkowitej energii mechanicznej
Wówczas zmiany całkowitej energii mechanicznej 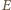 podczas ruchu możemy zapisać jako:
podczas ruchu możemy zapisać jako: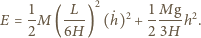
 zawieszonej na sprężynie o stałej sprężystości
zawieszonej na sprężynie o stałej sprężystości 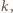 jeśli przyjmiemy:
jeśli przyjmiemy: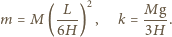
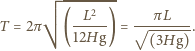
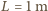 i
i 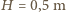
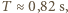 natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć
natomiast, na przykład, dla Jeziora Genewskiego, dla którego można przyjąć 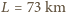 i średnią głębokość
i średnią głębokość 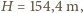 obliczone
obliczone 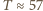 minut (obserwowano fale o
minut (obserwowano fale o 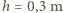 i
i 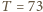 minuty).
minuty).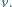 Przy jakiej prędkości
Przy jakiej prędkości  ruchu łopatek koła elektrownia osiąga maksymalną moc? Dla uproszczenia pomińmy efekty związane z zanurzaniem i wynurzaniem łopatek i zmiany ich ustawienia względem prędkości rzeki.
ruchu łopatek koła elektrownia osiąga maksymalną moc? Dla uproszczenia pomińmy efekty związane z zanurzaniem i wynurzaniem łopatek i zmiany ich ustawienia względem prędkości rzeki.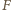 działająca na łopatkę będzie miała postać:
działająca na łopatkę będzie miała postać: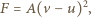
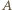 zależy od kształtu opływanego ciała, jego rozmiarów i od gęstości cieczy. "Pobierana" przez koło moc
zależy od kształtu opływanego ciała, jego rozmiarów i od gęstości cieczy. "Pobierana" przez koło moc 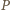 będzie więc równa:
będzie więc równa: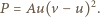
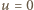 lub
lub  Pochodna
Pochodna 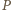 względem
względem  :
: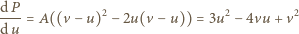
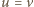 oraz dla
oraz dla 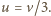 Jak łatwo sprawdzić, maksymalna moc osiągana jest dla
Jak łatwo sprawdzić, maksymalna moc osiągana jest dla 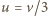 i wynosi:
i wynosi: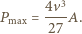
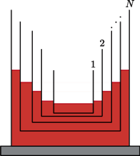
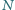 cylindrycznych naczyń o masach
cylindrycznych naczyń o masach 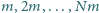 i przekrojach poprzecznych
i przekrojach poprzecznych 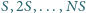 umieszczono jedno w drugim jak na rysunku. Do naczyń nalano tyle wody, że każde z nich pływa w większym naczyniu nie dotykając jego dna i ścianek. Największe naczynie stoi na stole. Do jakiej wysokości, w stosunku do powierzchni stołu, jest napełnione największe naczynie? Całkowita masa wody wynosi
umieszczono jedno w drugim jak na rysunku. Do naczyń nalano tyle wody, że każde z nich pływa w większym naczyniu nie dotykając jego dna i ścianek. Największe naczynie stoi na stole. Do jakiej wysokości, w stosunku do powierzchni stołu, jest napełnione największe naczynie? Całkowita masa wody wynosi 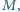 a jej gęstość wynosi
a jej gęstość wynosi 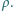 Ścianki naczyń uznać za zaniedbywalnie cienkie.
Ścianki naczyń uznać za zaniedbywalnie cienkie.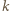 -tego naczynia. Z prawa Archimedesa wynika, że jeżeli wyjmiemy (w myśli) wszystkie naczynia pływające w
-tego naczynia. Z prawa Archimedesa wynika, że jeżeli wyjmiemy (w myśli) wszystkie naczynia pływające w 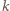 -tym naczyniu i dolejemy do niego tyle cieczy, aby zachować jej poziom wyjściowy, to siły działające na dno i ścianki naczynia ze strony cieczy w której ono pływa nie ulegną zmianie. Na
-tym naczyniu i dolejemy do niego tyle cieczy, aby zachować jej poziom wyjściowy, to siły działające na dno i ścianki naczynia ze strony cieczy w której ono pływa nie ulegną zmianie. Na 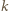 -te naczynie działa siła ciężkości
-te naczynie działa siła ciężkości 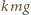 (
( 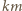 - masa tego naczynia), ciężar nalanej do niego wody
- masa tego naczynia), ciężar nalanej do niego wody 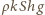 (
( 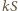 - pole powierzchni dna,
- pole powierzchni dna, 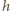 - wysokość poziomu wody w tym naczyniu) i siła wyporu
- wysokość poziomu wody w tym naczyniu) i siła wyporu 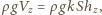 gdzie
gdzie 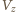 - objętość zanurzonej części naczynia,
- objętość zanurzonej części naczynia, 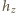 - głębokość zanurzenia.
- głębokość zanurzenia.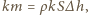 gdzie
gdzie 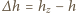 - różnica poziomów wody w rozpatrywanym naczyniu i w naczyniu w którym rozpatrywane naczynie pływa. Stąd
- różnica poziomów wody w rozpatrywanym naczyniu i w naczyniu w którym rozpatrywane naczynie pływa. Stąd 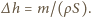 Wynika z tego, że różnica poziomów wody w dwóch dowolnych, sąsiednich naczyniach jest dla wszystkich naczyń taka sama. Przyjmijmy, że poziom wody w naczyniu stojącym na stole wynosi
Wynika z tego, że różnica poziomów wody w dwóch dowolnych, sąsiednich naczyniach jest dla wszystkich naczyń taka sama. Przyjmijmy, że poziom wody w naczyniu stojącym na stole wynosi 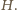 W następnym naczyniu wynosi on
W następnym naczyniu wynosi on 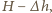 w kolejnym
w kolejnym 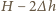 itd. Całkowita objętość wody w naczyniach wynosi
itd. Całkowita objętość wody w naczyniach wynosi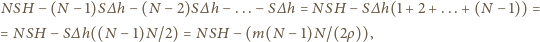
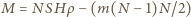
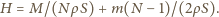
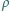 obraca wirnik turbiny. Jaka
maksymalna moc może być przekazana wirnikowi? Przed wirnikiem,
z dala od niego, ciecz porusza się z prędkością
obraca wirnik turbiny. Jaka
maksymalna moc może być przekazana wirnikowi? Przed wirnikiem,
z dala od niego, ciecz porusza się z prędkością
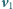 prostopadle do
płaszczyzny wirnika. Każda z łopat wirnika zakreśla podczas pełnego obrotu
powierzchnię
prostopadle do
płaszczyzny wirnika. Każda z łopat wirnika zakreśla podczas pełnego obrotu
powierzchnię
 Przyjmij, że wirnik jest cienki, a jego masa jest bardzo
mała.
Przyjmij, że wirnik jest cienki, a jego masa jest bardzo
mała.
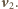 Moc przekazana
wirnikowi turbiny równa jest stracie energii kinetycznej w jednostce
czasu
Moc przekazana
wirnikowi turbiny równa jest stracie energii kinetycznej w jednostce
czasu
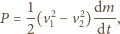
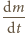 oznacza masę cieczy przepływającej przez powierzchnię wirnika
w jednostce czasu. Z drugiej strony, moc ta równa jest iloczynowi siły
oznacza masę cieczy przepływającej przez powierzchnię wirnika
w jednostce czasu. Z drugiej strony, moc ta równa jest iloczynowi siły
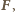 z jaką ciecz działa na wirnik (siła ta jest przeciwna do siły działającej na
ciecz), i prędkości
z jaką ciecz działa na wirnik (siła ta jest przeciwna do siły działającej na
ciecz), i prędkości
 przepływu cieczy przez powierzchnię
przepływu cieczy przez powierzchnię
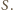 Siła
Siła
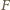 równa jest zmianie pędu cieczy w jednostce czasu, czyli
równa jest zmianie pędu cieczy w jednostce czasu, czyli
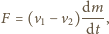 a więc
a więc
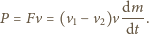
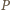 i korzystając ze współliniowości
wektorów
i korzystając ze współliniowości
wektorów
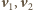 i
i
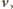 wnioskujemy, że
wnioskujemy, że
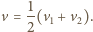 Otrzymujemy zatem
Otrzymujemy zatem
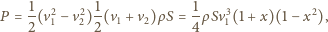
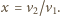 Jak łatwo sprawdzić, dla
Jak łatwo sprawdzić, dla
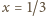 moc
moc
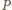 osiąga wartość maksymalną, która wynosi
osiąga wartość maksymalną, która wynosi
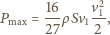
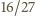 energii docierającej przez powierzchnię
energii docierającej przez powierzchnię
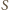 w
jednostce czasu.
w
jednostce czasu.
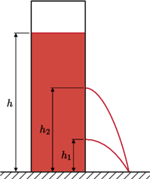
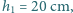 a drugi na wysokości
a drugi na wysokości
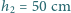 powyżej podstawy zbiornika. Strugi wody wypływającej ze
zbiornika przez te otwory trafiają w to samo miejsce na wysokości podstawy. Ile
wynosi poziom wody w zbiorniku?
powyżej podstawy zbiornika. Strugi wody wypływającej ze
zbiornika przez te otwory trafiają w to samo miejsce na wysokości podstawy. Ile
wynosi poziom wody w zbiorniku?
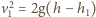 i
i
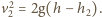 Cząsteczki wody poruszają się
w pionie ruchem jednostajnie przyspieszonym, zatem czas ich lotu od
otworu do wysokości podstawy zbiornika wynosi
Cząsteczki wody poruszają się
w pionie ruchem jednostajnie przyspieszonym, zatem czas ich lotu od
otworu do wysokości podstawy zbiornika wynosi
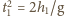 i
i
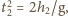 odpowiednio dla pierwszej i drugiej strugi. Zasięgi obu strug są
równe, tj.
odpowiednio dla pierwszej i drugiej strugi. Zasięgi obu strug są
równe, tj.
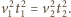 Łącząc uzyskane rezultaty, otrzymujemy
Łącząc uzyskane rezultaty, otrzymujemy
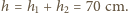

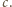 Dla wody
Dla wody
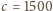 m/s.
Zmiana prędkości wody wywołana zamknięciem zaworu w czasie
m/s.
Zmiana prędkości wody wywołana zamknięciem zaworu w czasie
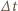 dotrze na odległość
dotrze na odległość
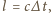 zatrzymana zostanie
masa wody
zatrzymana zostanie
masa wody
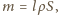 gdzie
gdzie
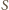 jest polem przekroju rury,
a
jest polem przekroju rury,
a
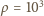 kg/m
kg/m
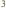 oznacza gęstość wody. Zmiana pędu
wody wynosi
oznacza gęstość wody. Zmiana pędu
wody wynosi
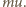 Ciśnienie
Ciśnienie
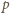 wody na zawór wyniesie
więc
wody na zawór wyniesie
więc
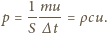
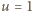 m/s ciśnienie jest równe
m/s ciśnienie jest równe

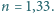 Jaką wartość musi mieć kąt
Jaką wartość musi mieć kąt
 między podstawą
a ścianką naczynia, aby przez boczną ściankę nie było widać monety
umieszczonej pod dnem naczynia?
między podstawą
a ścianką naczynia, aby przez boczną ściankę nie było widać monety
umieszczonej pod dnem naczynia?

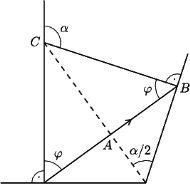
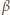 będzie kątem załamania promienia przechodzącego z warstwy
powietrza między monetą a dnem naczynia do wody (
będzie kątem załamania promienia przechodzącego z warstwy
powietrza między monetą a dnem naczynia do wody (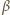 nie przekracza wartości kąta granicznego
nie przekracza wartości kąta granicznego
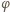 :
:
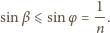
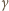 nie wyjdzie
na zewnątrz, gdy
nie wyjdzie
na zewnątrz, gdy
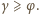 Zmniejszenie kąta
Zmniejszenie kąta
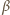 powoduje
zwiększenie kąta
powoduje
zwiększenie kąta
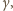 wystarczy więc rozważyć przypadek graniczny, gdy
wystarczy więc rozważyć przypadek graniczny, gdy
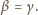 Rozważmy sytuację, gdy oba kąty
Rozważmy sytuację, gdy oba kąty
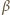 i
i
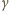 mają
wartość graniczną. W trójkącie
mają
wartość graniczną. W trójkącie
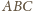 na
na 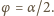 Zatem nie zobaczymy monety przez boczną ściankę, gdy
Zatem nie zobaczymy monety przez boczną ściankę, gdy
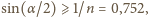 czyli
czyli
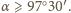
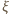 względem wierzchołka stożka. Równowaga
siły ciężkości i wyporu prowadzi do warunku
względem wierzchołka stożka. Równowaga
siły ciężkości i wyporu prowadzi do warunku
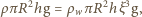
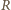 jest promieniem podstawy stożka,
jest promieniem podstawy stożka,
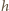 jego wysokością,
a
jego wysokością,
a
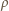 i
i
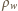 gęstościami odpowiednio lodu i wody. Stąd
gęstościami odpowiednio lodu i wody. Stąd
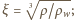 podstawiając
podstawiając
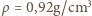 i
i
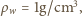 stwierdzamy,
że zanurzona część wysokości to
stwierdzamy,
że zanurzona część wysokości to
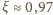 wysokości góry,
a zatem nad powierzchnię wystaje zaledwie około
wysokości góry,
a zatem nad powierzchnię wystaje zaledwie około
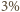 wysokości
góry.
wysokości
góry.
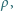 prostopadłościenny klocek o wymiarach
prostopadłościenny klocek o wymiarach
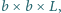 przy czym
przy czym
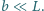 Zrobiono to tak zmyślnie, że najmniejsze ściany klocka mogą
ślizgać się bez tarcia po pionowych ścianach wanny, krawędzie o długości
Zrobiono to tak zmyślnie, że najmniejsze ściany klocka mogą
ślizgać się bez tarcia po pionowych ścianach wanny, krawędzie o długości
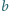 są pionowe lub poziome, a siła grawitacji działająca na klocek
równoważy siłę wyporu. Czy klocek jest w położeniu równowagi
trwałej?
są pionowe lub poziome, a siła grawitacji działająca na klocek
równoważy siłę wyporu. Czy klocek jest w położeniu równowagi
trwałej?
 i
i
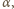 zaznaczone na rysunku.
zaznaczone na rysunku.
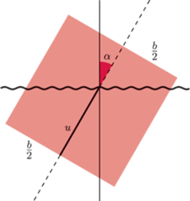
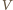 możemy
wyrazić jako różnicę energii potencjalnej grawitacji, równej
możemy
wyrazić jako różnicę energii potencjalnej grawitacji, równej
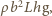 oraz energii potencjalnej, jaką miała wyparta przez klocek woda,
równej
oraz energii potencjalnej, jaką miała wyparta przez klocek woda,
równej
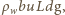 gdzie
gdzie
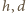 są odpowiednio wysokościami
środka ciężkości klocka i jego zanurzonej części nad poziomem wody.
Wielkości te są równe odpowiednio:
są odpowiednio wysokościami
środka ciężkości klocka i jego zanurzonej części nad poziomem wody.
Wielkości te są równe odpowiednio:
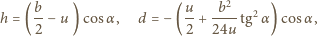
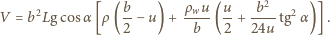
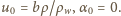 Dla małych wychyleń z położenia równowagi
mamy
Dla małych wychyleń z położenia równowagi
mamy
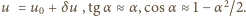 Podstawiając do
powyższego wzoru i ograniczając się do wyrazów kwadratowych
w
Podstawiając do
powyższego wzoru i ograniczając się do wyrazów kwadratowych
w
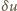 i
i
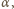 otrzymujemy:
otrzymujemy:
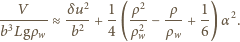
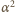 jest dodatni dla
jest dodatni dla
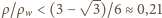 lub
lub
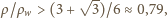 wtedy mamy do czynienia z minimum
energii potencjalnej i rozważana sytuacja odpowiada równowadze
trwałej.
wtedy mamy do czynienia z minimum
energii potencjalnej i rozważana sytuacja odpowiada równowadze
trwałej.
 promień kulki, przez
promień kulki, przez
 jej prędkość
i przez
jej prędkość
i przez
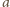 przyspieszenie. Przyjmijmy realistyczne założenie, że
gęstość gliceryny to
przyspieszenie. Przyjmijmy realistyczne założenie, że
gęstość gliceryny to
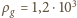 kg/m
kg/m
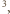 gęstość szkła
gęstość szkła
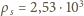 kg/m
kg/m
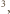 a lepkość dynamiczna jest równa
a lepkość dynamiczna jest równa
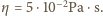 Równanie ruchu kulki w cieczy jest następujące:
Równanie ruchu kulki w cieczy jest następujące:
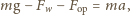
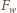 jest siłą wyporu, a
jest siłą wyporu, a
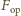 siłą oporów ruchu działającą na
kulkę. Jeżeli założymy, iż lepkość gliceryny jest tak duża, że można
posługiwać się prawem Stokesa, będziemy mieli
siłą oporów ruchu działającą na
kulkę. Jeżeli założymy, iż lepkość gliceryny jest tak duża, że można
posługiwać się prawem Stokesa, będziemy mieli
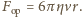 Stąd oraz
z prawa Archimedesa otrzymamy wyrażenie, z którego można wyznaczyć
przyspieszenie kulki:
Stąd oraz
z prawa Archimedesa otrzymamy wyrażenie, z którego można wyznaczyć
przyspieszenie kulki: