O LXIII Olimpiadzie Matematycznej»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: LXIII Olimpiada Matematyczna
- Zadanie pochodzi z artykułu O LXIII Olimpiadzie Matematycznej
- Publikacja w Delcie: maj 2012
- Publikacja elektroniczna: 28-04-2012
- Artykuł źródłowy w wersji do druku [application/pdf]: (65 KB)
Udowodnić, że w czworościanie
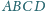 wierzchołek
wierzchołek
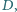 środek
sfery wpisanej oraz środek ciężkości czworościanu leżą na jednej prostej
wtedy i tylko wtedy, gdy pola trójkątów
środek
sfery wpisanej oraz środek ciężkości czworościanu leżą na jednej prostej
wtedy i tylko wtedy, gdy pola trójkątów
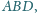
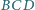 i
i
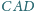 są równe.
są równe.
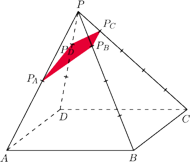
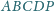 jest równoległobok
jest równoległobok
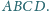 Punkty
Punkty
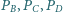 na krawędziach
na krawędziach
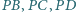 spełniają warunki:
spełniają warunki:
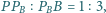
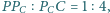
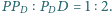 Płaszczyzna
Płaszczyzna
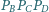 przecina krawędź
przecina krawędź
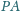 w punkcie
w punkcie
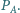 Wyznacz
Wyznacz
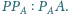
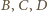 masy odpowiednio
masy odpowiednio
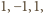 a w punkcie
a w punkcie
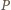 trzy masy:
trzy masy:
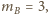
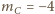 i
i
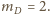 Wtedy
Wtedy
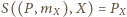 dla
dla
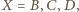 więc środek ciężkości
więc środek ciężkości
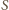 układu
układu
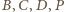 leży na płaszczyźnie
leży na płaszczyźnie
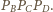 Ponadto
Ponadto
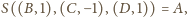 bo
bo
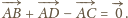 Skoro
Skoro
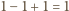 oraz
oraz
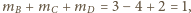 to
to
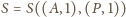 jest środkiem odcinka
jest środkiem odcinka
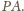 Stąd
i z wcześniejszego
Stąd
i z wcześniejszego
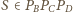 wynika
wynika
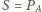 i
i
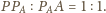
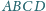 i
i
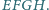 Płaszczyzna
przecina jego krawędzie boczne
Płaszczyzna
przecina jego krawędzie boczne
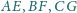 i
i
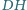 odpowiednio
w punktach
odpowiednio
w punktach
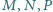 i
i
 Wykaż, że
Wykaż, że

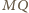 i
i
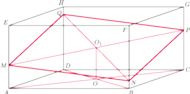
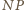 zawierają się w jednej płaszczyźnie
i jednocześnie zawierają się w płaszczyznach równoległych, więc są to odcinki
równoległe. Analogicznie równoległe są odcinki
zawierają się w jednej płaszczyźnie
i jednocześnie zawierają się w płaszczyznach równoległych, więc są to odcinki
równoległe. Analogicznie równoległe są odcinki
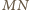 i
i
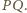 Stąd
czworokąt
Stąd
czworokąt
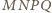 jest równoległobokiem.
jest równoległobokiem.
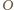 będzie punktem przecięcia przekątnych
będzie punktem przecięcia przekątnych
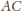 i
i
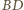 podstawy
podstawy
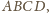 a
a
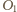 – punktem
przecięcia przekątnych
– punktem
przecięcia przekątnych
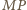 i
i
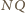 równoległoboku
równoległoboku
 Zauważmy, że odcinek
Zauważmy, że odcinek
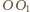 jest odcinkiem
łączącym środki nierównoległych boków trapezów
jest odcinkiem
łączącym środki nierównoległych boków trapezów
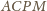 i
i
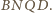 Jest on równoległy do boków równoległych tych trapezów
oraz
Jest on równoległy do boków równoległych tych trapezów
oraz
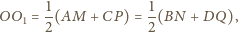
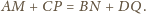
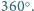
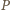 będzie
dowolnym punktem leżącym wewnątrz danego kąta trójściennego, a
będzie
dowolnym punktem leżącym wewnątrz danego kąta trójściennego, a
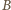 i
i
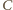 jego rzutami prostokątnymi na płaszczyzny
zawierające ściany danego kąta trójściennego. Jeśli
jego rzutami prostokątnymi na płaszczyzny
zawierające ściany danego kąta trójściennego. Jeśli
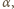
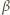 i
i
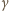 oznaczają miary kątów dwuściennych,
to miary kątów płaskich
oznaczają miary kątów dwuściennych,
to miary kątów płaskich
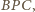
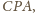
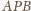 są równe
są równe
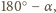
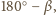
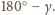
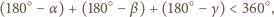
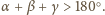
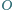 jest środkiem sfery wpisanej w czworościan
jest środkiem sfery wpisanej w czworościan
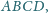 przy czym prosta
przy czym prosta
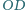 jest prostopadła do krawędzi
jest prostopadła do krawędzi
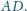 Znaleźć miarę kąta dwuściennego między płaszczyznami
Znaleźć miarę kąta dwuściennego między płaszczyznami
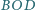 i
i
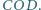
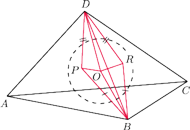
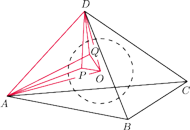
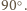 Niech
Niech
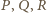 będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
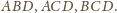 Z równości
Z równości
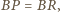
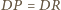 i
i
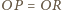 wnioskujemy, że czworościany
wnioskujemy, że czworościany
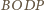 i
i
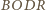 są przystające (
są przystające (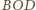 i
i
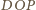 jest równy kątowi dwuściennemu
między płaszczyznami
jest równy kątowi dwuściennemu
między płaszczyznami
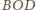 i
i
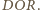 Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
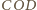 i
i
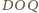 jest
równy kątowi dwuściennemu między płaszczyznami
jest
równy kątowi dwuściennemu między płaszczyznami
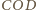 i
i
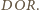 Wykażemy, że punkty
Wykażemy, że punkty
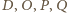 leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
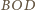 i
i
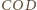 ma miarę
ma miarę
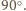
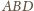 jest prostopadła do prostej
jest prostopadła do prostej
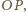 to
to
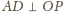 (
(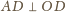 dostajemy
dostajemy
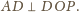 Analogicznie udowodnimy, że
Analogicznie udowodnimy, że
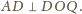 Zatem punkty
Zatem punkty
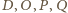 leżą na jednej
płaszczyźnie prostopadłej do krawędzi
leżą na jednej
płaszczyźnie prostopadłej do krawędzi
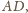 co kończy dowód.
co kończy dowód.
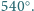
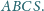 Krawędzie podstawy mają
długości
Krawędzie podstawy mają
długości
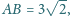
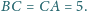 Krawędzie boczne mają
długości
Krawędzie boczne mają
długości
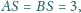
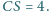 Oblicz objętość tego
ostrosłupa.
Oblicz objętość tego
ostrosłupa.
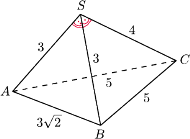
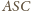 jest trójkątem o bokach długości
jest trójkątem o bokach długości
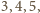 ma zatem
kąt prosty przy wierzchołku
ma zatem
kąt prosty przy wierzchołku
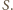 Analogicznie
Analogicznie
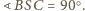 Ściana
Ściana
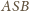 ma boki długości
ma boki długości
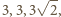 czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
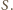 Ustawmy dany
ostrosłup inaczej: niech
Ustawmy dany
ostrosłup inaczej: niech
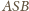 będzie podstawą. Wobec powyższych
obserwacji
będzie podstawą. Wobec powyższych
obserwacji
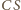 jest wtedy wysokością i
jest wtedy wysokością i
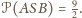 Stąd
objętość ostrosłupa to
Stąd
objętość ostrosłupa to
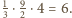
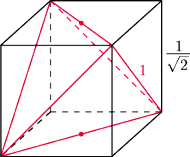
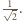 Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
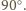 Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
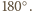 W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
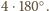 Sprzeczność, gdyż ta suma jest równa
Sprzeczność, gdyż ta suma jest równa
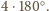
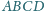 kąty
kąty
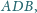
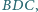
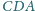 są
rozwarte, a krawędzie
są
rozwarte, a krawędzie
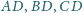 są równe. Dowieść, że trójkąt
są równe. Dowieść, że trójkąt
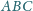 jest ostrokątny.
jest ostrokątny.
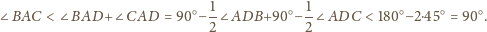
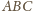 są ostre.
są ostre.
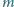 będzie liczbą krawędzi czworościanu o długości
będzie liczbą krawędzi czworościanu o długości
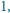 a
a
 liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
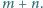
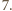
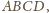 w którym
w którym
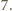 Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
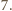 Wynika stąd w szczególności, że liczba krawędzi
długości
Wynika stąd w szczególności, że liczba krawędzi
długości
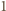 jest równa co najmniej
jest równa co najmniej
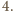 Jeśli jest
Jeśli jest
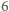 krawędzi
długości
krawędzi
długości
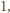 to nie ma kątów rozwartych. Jeśli jest
to nie ma kątów rozwartych. Jeśli jest
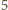 krawędzi
długości
krawędzi
długości
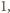 to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
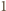 musi być równa
musi być równa
 Tym samym
liczba kątów rozwartych musi być równa
Tym samym
liczba kątów rozwartych musi być równa
 Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
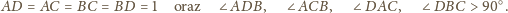
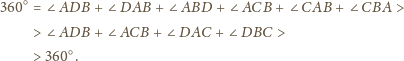
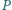 będzie dowolnym punktem wewnątrz czworościanu
będzie dowolnym punktem wewnątrz czworościanu
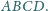 Dowieść, że
Dowieść, że

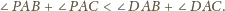
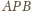 przecina krawędź
przecina krawędź
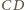 w
punkcie
w
punkcie
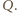 Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
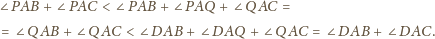
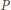 leży wewnątrz trójkąta
leży wewnątrz trójkąta
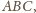 to
to
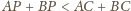 –
wystarczy rozważyć sferę o środku
–
wystarczy rozważyć sferę o środku
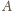 i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
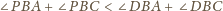
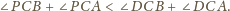
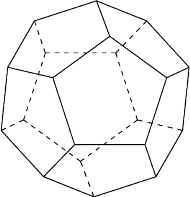
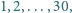 używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była: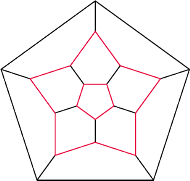
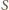 oznacza sumę wszystkich numerów
krawędzi:
oznacza sumę wszystkich numerów
krawędzi:
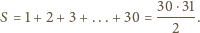
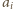 oznacza sumę numerów w
oznacza sumę numerów w
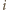 -tym wierzchołku (
-tym wierzchołku (
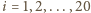 ). Wtedy
). Wtedy
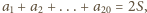 bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
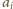 była podzielna przez 4, to
była podzielna przez 4, to
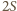 także. Jednak
także. Jednak
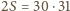 nie dzieli się przez 4.
nie dzieli się przez 4.
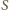 oznacza ich sumę, a
oznacza ich sumę, a
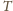 – sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
– sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
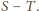 Początkowo
Początkowo
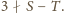 Tymczasem gdyby
Tymczasem gdyby
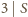 i
i
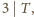 to
to
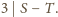
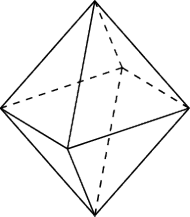
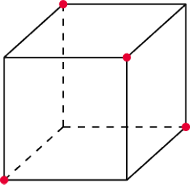
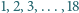 można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.
można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.
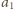 i
i
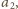
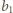 i
i
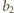 oraz
oraz
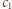 i
i
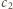 liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
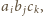 gdzie
gdzie
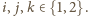 Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako
Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako