Numerowanie»Zadanie 5
o zadaniu...
- Zadanie olimpijskie: XLV Olimpiada Matematyczna.
- Zadanie pochodzi z artykułu Numerowanie
- Publikacja w Delcie: kwiecień 2011
- Publikacja elektroniczna: 31-03-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (109 KB)
Każdemu wierzchołkowi sześcianu przyporządkowano liczbę 1 lub
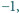 a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
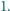 Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
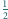 w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
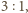 licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
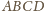 można wpisać kulę
można wpisać kulę
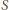 o środku
o środku
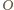 i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
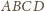 przez jednokładność względem punktu
przez jednokładność względem punktu
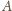 o skali
o skali
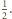 W efekcie otrzymamy czworościan
W efekcie otrzymamy czworościan
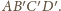 Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
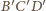 przecina wysokość
przecina wysokość
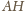 w punkcie
w punkcie
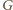 w taki
sposób, że
w taki
sposób, że
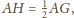 a kula
a kula
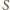 jest również styczna do
płaszczyzny
jest również styczna do
płaszczyzny
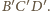 Zatem kula
Zatem kula
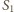 wpisana w czworościan
wpisana w czworościan
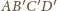 ma promień
ma promień
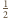 i ma tylko jeden punkt wspólny z kulą
i ma tylko jeden punkt wspólny z kulą
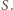
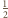 umieszczone w każdym „rogu” czworościanu
umieszczone w każdym „rogu” czworościanu
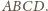 Każda z tych kul
ma tylko jeden punkt wspólny z kulą
Każda z tych kul
ma tylko jeden punkt wspólny z kulą
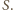 Ponieważ kula
Ponieważ kula
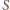 ma
promień 1, więc można umieścić w niej dwie kule o promieniu
ma
promień 1, więc można umieścić w niej dwie kule o promieniu
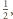 które mają tylko jeden punkt wspólny.
które mają tylko jeden punkt wspólny.
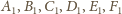 będą odpowiednio środkami krawędzi
będą odpowiednio środkami krawędzi
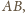
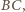
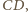
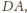
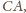
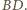 Przekształćmy kulę
Przekształćmy kulę
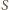 i czworościan
i czworościan
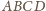 przez
przez 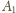 i skali
i skali
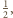
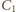 i skali
i skali
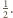
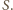 Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
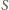 przez
przez 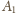 i skali
i skali
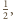
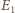 i skali
i skali
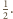
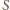 będą środki kul o promieniach
będą środki kul o promieniach
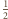 znajdujące się w połowie odcinków
znajdujące się w połowie odcinków
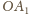 i
i
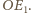 Wykażemy teraz,
że kule te nie mają punktów wspólnych.
Wykażemy teraz,
że kule te nie mają punktów wspólnych.
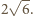 Zatem odległość
punktów
Zatem odległość
punktów
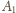 i
i
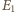 wynosi
wynosi
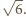 Środki boków
Środki boków
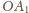 i
i
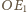 w trójkącie
w trójkącie
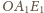 pozostają w odległości
pozostają w odległości
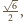 która
jest większa od 1.
która
jest większa od 1.
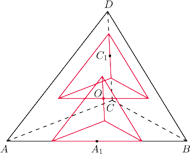
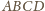 można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
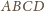 w
jednokładności o skali
w
jednokładności o skali
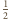 i środku będącym środkiem krawędzi
czworościanu.
i środku będącym środkiem krawędzi
czworościanu.
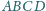 jest styczna do ścian
jest styczna do ścian
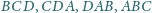 odpowiednio w punktach
odpowiednio w punktach
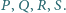 Odcinek
Odcinek
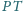 jest średnicą tej sfery, zaś punkty
jest średnicą tej sfery, zaś punkty
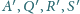 są
punktami przecięcia prostych
są
punktami przecięcia prostych
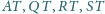 z płaszczyzną
z płaszczyzną
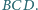 Dowieść , że punkt
Dowieść , że punkt
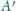 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
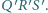
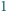 od jego wierzchołków jest
nie większa niż
od jego wierzchołków jest
nie większa niż
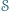 jest styczna do krawędzi
jest styczna do krawędzi
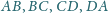 czworościanu
czworościanu
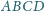 dpowiednio w punktach
dpowiednio w punktach
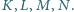 Wykaż, że leżą one
na jednej płaszczyźnie.
Wykaż, że leżą one
na jednej płaszczyźnie.
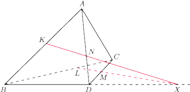
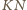 przecina prostą
przecina prostą
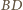 w pewnym punkcie
w pewnym punkcie
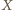 (poza odcinkiem
(poza odcinkiem
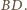 Wtedy z twierdzenia Menelaosa dla
trójkąta
Wtedy z twierdzenia Menelaosa dla
trójkąta
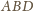 i prostej
i prostej
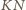 mamy
mamy
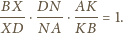
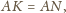
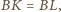
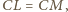
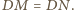 Wobec powyższego
Wobec powyższego
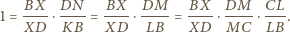
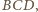 prosta
prosta
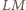 przecina prostą
przecina prostą
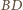 w punkcie
w punkcie
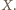 Stąd proste
Stąd proste
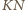 i
i
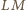 przecinają się, więc punkty
przecinają się, więc punkty
 leżą na jednej
płaszczyźnie. Prostszy przypadek
leżą na jednej
płaszczyźnie. Prostszy przypadek
 pozostawiam jako
ćwiczenie.
pozostawiam jako
ćwiczenie.
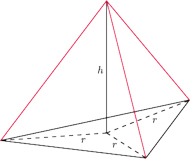
 oraz
długość krawędzi wychodzących z wierzchołka
oraz
długość krawędzi wychodzących z wierzchołka
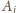 przez
przez
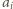 ,
gdzie
,
gdzie
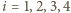 . Wtedy krawędź
. Wtedy krawędź
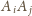 , gdzie
, gdzie
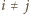 ,
wychodzi z wierzchołka
,
wychodzi z wierzchołka
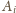 oraz z wierzchołka
oraz z wierzchołka
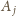 . Oznacza to,
że
. Oznacza to,
że
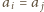 , a więc czworościan jest foremny.
, a więc czworościan jest foremny.
 (licząc
od wierzchołków) leżą na jednej sferze.
(licząc
od wierzchołków) leżą na jednej sferze.
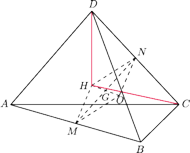
 niech
niech
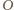 będzie
środkiem sfery opisanej, a
będzie
środkiem sfery opisanej, a
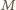 i
i
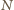 – środkami krawędzi
– środkami krawędzi
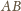 i
i
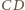 . Przez
. Przez
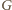 oznaczmy środek odcinka
oznaczmy środek odcinka
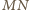 ,
czyli środek ciężkości czworościanu
,
czyli środek ciężkości czworościanu
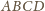 . Niech
. Niech
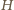 będzie
punktem symetrycznym do
będzie
punktem symetrycznym do
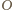 względem
względem
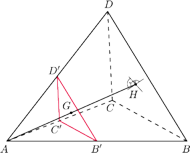
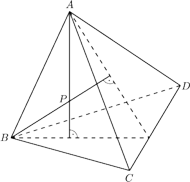
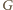 (rysunek). Punkty
(rysunek). Punkty
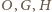 leżą wtedy na jednej prostej, a
leżą wtedy na jednej prostej, a
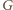 jest środkiem
odcinka
jest środkiem
odcinka
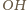 . Wobec tego chcemy wykazać, że
. Wobec tego chcemy wykazać, że
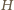 jest
ortocentrum czworościanu
jest
ortocentrum czworościanu
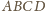 .
.
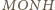 jest równoległobokiem.
W szczególności proste
jest równoległobokiem.
W szczególności proste
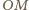 i
i
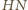 są równoległe. Z definicji
punktów
są równoległe. Z definicji
punktów
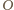 i
i
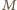 wynika, że odcinki
wynika, że odcinki
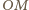 i
i
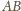 są
prostopadłe, więc również
są
prostopadłe, więc również
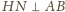 . Stąd i z prostopadłości
prostych
. Stąd i z prostopadłości
prostych
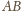 i
i
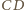 (
(
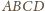 jest ortocentryczny!)
wynika, że płaszczyzna
jest ortocentryczny!)
wynika, że płaszczyzna
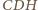 jest prostopadła do prostej
jest prostopadła do prostej
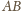 .
W takim razie prosta
.
W takim razie prosta
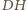 jest prostopadła do prostej
jest prostopadła do prostej
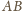 .
Analogicznie dowodzimy, że
.
Analogicznie dowodzimy, że
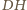 jest prostopadła również do
prostej
jest prostopadła również do
prostej
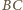 .
.
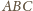 , czyli
stanowi wysokość czworościanu
, czyli
stanowi wysokość czworościanu
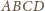 . Podobnie dowodzimy, że
proste
. Podobnie dowodzimy, że
proste
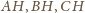 są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
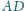 czworościanu
czworościanu
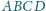 jest prostopadła do
płaszczyzny
jest prostopadła do
płaszczyzny
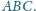 Wykazać, że rzut prostokątny ortocentrum
trójkąta
Wykazać, że rzut prostokątny ortocentrum
trójkąta
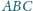 na płaszczyznę
na płaszczyznę
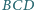 jest ortocentrum trójkąta
jest ortocentrum trójkąta
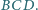
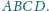 Dowieść, że krawędzie
Dowieść, że krawędzie
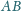 i
i
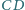 są prostopadłe wtedy i tylko wtedy, gdy istnieje w przestrzeni
taki równoległobok
są prostopadłe wtedy i tylko wtedy, gdy istnieje w przestrzeni
taki równoległobok
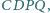 że
że
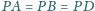 oraz
oraz
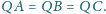
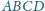 wysokości
poprowadzone z wierzchołków
wysokości
poprowadzone z wierzchołków
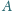 i
i
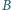 przecinają się, to również
wysokości poprowadzone z wierzchołków
przecinają się, to również
wysokości poprowadzone z wierzchołków
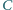 i
i
 przecinają
się.
przecinają
się.
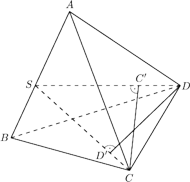
 będzie punktem przecięcia wysokości czworościanu
poprowadzonych z wierzchołków
będzie punktem przecięcia wysokości czworościanu
poprowadzonych z wierzchołków
 i
i
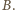 Mamy
Mamy
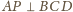 ,
więc też
,
więc też
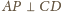 i analogicznie
i analogicznie
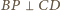 . W takim razie
płaszczyzna
. W takim razie
płaszczyzna
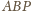 jest prostopadła do krawędzi
jest prostopadła do krawędzi
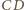 , w szczególności
, w szczególności
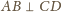 . Na prostej
. Na prostej
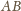 wybierzmy taki punkt
wybierzmy taki punkt
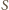 , że
, że
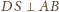 . Zatem płaszczyzna
. Zatem płaszczyzna
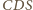 jest prostopadła do krawędzi
jest prostopadła do krawędzi
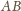 . Niech
. Niech
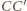 i
i
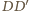 będą wysokościami trójkąta
będą wysokościami trójkąta
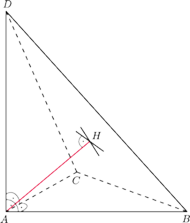
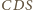 (rysunek obok). Prosta
(rysunek obok). Prosta
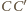 jest prostopadła zarówno
do
jest prostopadła zarówno
do
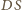 , jak i do
, jak i do
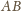 (bo leży w płaszczyźnie prostopadłej
do tej krawędzi). Jest więc wysokością czworościanu
(bo leży w płaszczyźnie prostopadłej
do tej krawędzi). Jest więc wysokością czworościanu
 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka
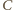 . Analogicznie dowodzimy, że również
. Analogicznie dowodzimy, że również
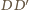 jest wysokością danego czworościanu. Te dwie proste mają punkt
wspólny będący ortocentrum trójkąta
jest wysokością danego czworościanu. Te dwie proste mają punkt
wspólny będący ortocentrum trójkąta
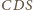 . Dowód jest więc
zakończony.
. Dowód jest więc
zakończony.
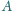 czworościanu
czworościanu
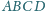 są proste. Wykazać, że rzut prostokątny
są proste. Wykazać, że rzut prostokątny
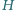 punktu
punktu
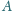 na
płaszczyznę
na
płaszczyznę
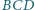 jest ortocentrum trójkąta
jest ortocentrum trójkąta
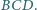
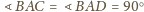 , to
, to
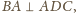 a więc
a więc
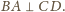 Ponadto
Ponadto
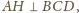 skąd
skąd
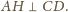 Zatem płaszczyzna
Zatem płaszczyzna
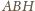 jest prostopadła do prostej
jest prostopadła do prostej
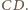 W takim razie
W takim razie
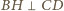 .
Analogicznie udowodnimy, że
.
Analogicznie udowodnimy, że
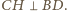 Zatem punkt
Zatem punkt
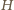 jest
ortocentrum trójkąta
jest
ortocentrum trójkąta
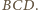
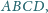 w którym
w którym
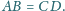 Sfera
wpisana w ten czworościan jest styczna do ścian
Sfera
wpisana w ten czworościan jest styczna do ścian
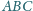 i
i
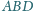 odpowiednio w punktach
odpowiednio w punktach
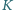 i
i
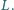 Dowieść, że jeżeli punkty
Dowieść, że jeżeli punkty
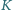 i
i
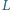 są środkami ciężkości ścian
są środkami ciężkości ścian
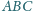 i
i
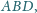 to czworościan
to czworościan
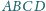 jest foremny.
jest foremny.
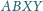 jest opisany na sferze. Punkty
jest opisany na sferze. Punkty
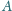 i
i
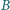 są
ustalone, a punkty
są
ustalone, a punkty
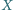 i
i
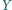 poruszają się. Udowodnić, że suma
kątów
poruszają się. Udowodnić, że suma
kątów

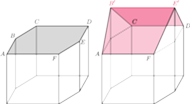
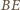 ściany
ściany
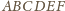 ).
).
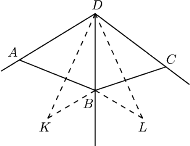
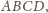 styczną do
ściany
styczną do
ściany
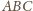 w punkcie
w punkcie
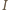 , który jest środkiem koła
wpisanego w trójkąt
, który jest środkiem koła
wpisanego w trójkąt
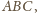 oraz styczną do płaszczyzn
oraz styczną do płaszczyzn
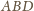 i
i
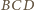 odpowiednio w punktach
odpowiednio w punktach
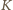 i
i
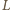 . Zauważmy, że
. Zauważmy, że
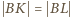 i
i
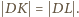
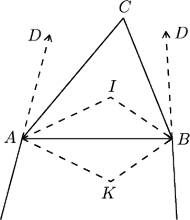
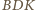 i
i
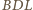 są przystające, a stąd
są przystające, a stąd
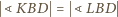
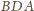 i
i
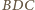 ,,rozłożone płasko”).
,,rozłożone płasko”).
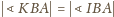 (rys.2) przedstawia
półpłaszczyzny
(rys.2) przedstawia
półpłaszczyzny
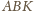 i
i
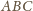 ,,rozłożone płasko”) – oraz że
,,rozłożone płasko”) – oraz że
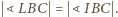
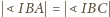 ; stąd
; stąd
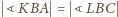 i w konsekwencji
i w konsekwencji
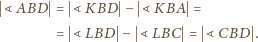
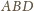 , stwierdzamy
analogicznie, że
, stwierdzamy
analogicznie, że
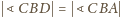 . Zatem wszystkie kąty płaskie ścian
przy wierzchołku
. Zatem wszystkie kąty płaskie ścian
przy wierzchołku
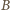 są równe:
są równe:
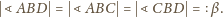
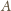 są równe (oznaczmy ich miarę przez
są równe (oznaczmy ich miarę przez
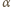 ), kąty przy wierzchołku
), kąty przy wierzchołku
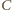 są równe
są równe
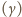 oraz kąty przy wierzchołku
oraz kąty przy wierzchołku
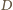 są równe
są równe
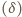 .
.
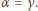 Analogicznie uzasadniamy, że
Analogicznie uzasadniamy, że
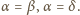 To znaczy, że wszystkie kąty
wszystkich ścian czworościanu są równe. Zatem ściany są trójkątami
równobocznymi i czworościan jest foremny.
To znaczy, że wszystkie kąty
wszystkich ścian czworościanu są równe. Zatem ściany są trójkątami
równobocznymi i czworościan jest foremny.