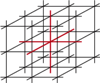
Czego jeszcze nie wiedzieliśmy o bryłach platońskich?
"Bryły platońskie" to inna nazwa wielościanów foremnych. W przestrzeni trójwymiarowej jest ich dokładnie 5 i są to: czworościan, sześcian, ośmiościan, dwunastościan oraz dwudziestościan foremny. Ich historia sięga czasów starożytnych i wydawałoby się, że po ponad dwóch tysiącach lat wiemy o nich już absolutnie wszystko.
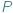 będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez
będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez 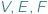 odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki
odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki 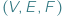 liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości:
liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości: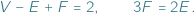
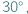 to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
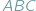 umieściliśmy trójkąt
umieściliśmy trójkąt 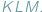 Wówczas pole
Wówczas pole 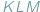 nie przekracza, oczywiście, pola
nie przekracza, oczywiście, pola 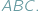 Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta
Czy możemy stwierdzić to samo o obwodach tych trójkątów? W tym przypadku słowo "oczywiście" również wydaje się uprawnione, Czytelnicy Delty z pewnością wiedzą jednak, jak łatwo o nadużycie tej formułki. Szczęśliwie w tej sytuacji nie pociągałoby to za sobą tragicznych konsekwencji, gdyż istotnie, również obwód trójkąta 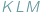 nie przekracza obwodu trójkąta
nie przekracza obwodu trójkąta 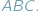
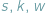 ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego
ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego 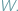 Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci
Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci
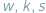 liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem
liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 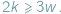 Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc
Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 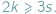 Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera:
Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: