Przecięcia płaszczyzn»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Przecięcia płaszczyzn
- Publikacja w Delcie: sierpień 2016
- Publikacja elektroniczna: 31 lipca 2016
-
Zadanie 1 pochodzi z gazetki Olimpiady Matematycznej Gimnazjalistów Kwadrat nr 7
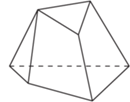
 i
i  oznaczają odpowiednio punkty przecięcia prostych
oznaczają odpowiednio punkty przecięcia prostych 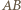 z
z 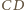 oraz
oraz 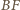 z
z 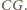 Wówczas każdy z punktów
Wówczas każdy z punktów 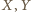 należy do obu płaszczyzn rozważanych powyżej ścian, a więc też do ich wspólnej prostej. Jednak punkty
należy do obu płaszczyzn rozważanych powyżej ścian, a więc też do ich wspólnej prostej. Jednak punkty 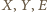 nie są współliniowe, zatem rysunek nie przedstawia wielościanu.
nie są współliniowe, zatem rysunek nie przedstawia wielościanu.
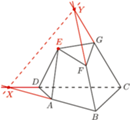
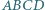 przecięto płaszczyzną, uzyskując w przekroju czworokąt
przecięto płaszczyzną, uzyskując w przekroju czworokąt 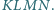 Na rysunku obok wyznacz punkt
Na rysunku obok wyznacz punkt  posługując się jedynie linijką.
posługując się jedynie linijką.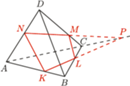
 punkt przecięcia prostych
punkt przecięcia prostych 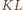 i
i 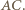 Punkt ten leży w płaszczyźnie przekroju, zatem leży w niej też prosta
Punkt ten leży w płaszczyźnie przekroju, zatem leży w niej też prosta 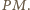 Stąd brakujący punkt
Stąd brakujący punkt  to punkt przecięcia prostych
to punkt przecięcia prostych 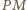 i
i 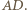
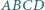 podstawa
podstawa 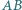 ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt
ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt 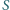 jest wierzchołkiem ostrosłupa o podstawie
jest wierzchołkiem ostrosłupa o podstawie 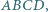 w którym
w którym 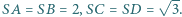 Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.
Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.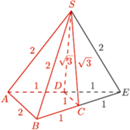
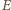 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 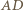 i
i 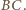 Z kształtu trapezu
Z kształtu trapezu 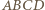 wynika, że
wynika, że 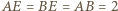 oraz że jego pole to
oraz że jego pole to 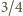 pola trójkąta
pola trójkąta 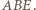
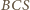 wnioskujemy, że jest on połową trójkąta równobocznego o krawędzi 2. Ponieważ
wnioskujemy, że jest on połową trójkąta równobocznego o krawędzi 2. Ponieważ 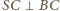 oraz
oraz 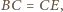 więc
więc 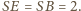
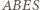 jest foremny o krawędzi 2. Jego objętość jest zatem 8-krotnie większa od objętości czworościanu foremnego o krawędzi 1, więc szukany stosunek objętości równy jest
jest foremny o krawędzi 2. Jego objętość jest zatem 8-krotnie większa od objętości czworościanu foremnego o krawędzi 1, więc szukany stosunek objętości równy jest 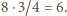
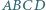 nie będący trapezem. Proste
nie będący trapezem. Proste 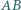 i
i 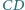 przecinają się w punkcie
przecinają się w punkcie  Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu
Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu  od płaszczyzny podstawy ostrosłupa.
od płaszczyzny podstawy ostrosłupa.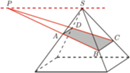
 leży w płaszczyźnie przedniej ściany ostrosłupa z rysunku, a prosta
leży w płaszczyźnie przedniej ściany ostrosłupa z rysunku, a prosta 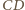 w płaszczyźnie tylnej ściany, więc punkt
w płaszczyźnie tylnej ściany, więc punkt 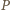 należy do obydwu tych płaszczyzn. Ich częścią wspólną jest prosta równoległa do podstawy ostrosłupa (gdyż jest on prawidłowy) i przechodząca przez wierzchołek
należy do obydwu tych płaszczyzn. Ich częścią wspólną jest prosta równoległa do podstawy ostrosłupa (gdyż jest on prawidłowy) i przechodząca przez wierzchołek 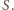 Stąd jedyną wartością, jaką może przyjąć odległość punktu
Stąd jedyną wartością, jaką może przyjąć odległość punktu 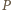 od płaszczyzny podstawy, jest wysokość ostrosłupa równa
od płaszczyzny podstawy, jest wysokość ostrosłupa równa 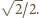
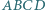 i krawędziach bocznych
i krawędziach bocznych  Wyznacz miarę kąta dwuściennego między płaszczyznami
Wyznacz miarę kąta dwuściennego między płaszczyznami 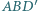 i
i 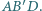
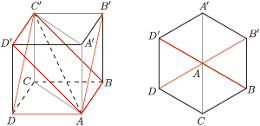
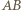 i
i 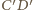 są równoległe, leżą więc w jednej płaszczyźnie
są równoległe, leżą więc w jednej płaszczyźnie 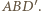 Stąd punkt
Stąd punkt 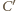 też do niej należy; podobnie należy on także do
też do niej należy; podobnie należy on także do 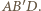 Punkty
Punkty 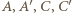 również leżą w jednej płaszczyźnie.
również leżą w jednej płaszczyźnie. i każda z nich zawiera inną z trzech krawędzi wychodzących z wierzchołka
i każda z nich zawiera inną z trzech krawędzi wychodzących z wierzchołka 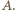 Oznacza to, że płaszczyzny te tworzą równe kąty dwuścienne, czyli kąty po
Oznacza to, że płaszczyzny te tworzą równe kąty dwuścienne, czyli kąty po 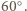
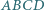 wpisanego w okrąg o środku
wpisanego w okrąg o środku 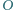 przecinają się w punkcie
przecinają się w punkcie 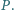 Niech
Niech 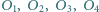 będą środkami okręgów opisanych odpowiednio na trójkątach
będą środkami okręgów opisanych odpowiednio na trójkątach 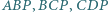 i
i 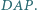 Wykazać, że proste
Wykazać, że proste 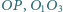 i
i 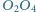 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
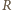 będzie punktem przecięcia prostej
będzie punktem przecięcia prostej 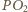 z prostą
z prostą 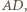 a
a 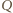 różnym od
różnym od 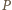 punktem przecięcia tej prostej z okręgiem opisanym na trójkącie
punktem przecięcia tej prostej z okręgiem opisanym na trójkącie 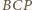 (rysunek). Wówczas
(rysunek). Wówczas 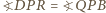 oraz
oraz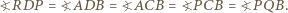
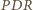 i
i 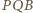 są podobne, w szczególności
są podobne, w szczególności 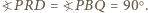 Stąd prosta
Stąd prosta 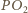 jest prostopadła do
jest prostopadła do 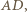 a więc również równoległa do
a więc również równoległa do 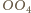 - symetralnej
- symetralnej 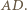 Analogicznie proste
Analogicznie proste 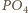 i
i 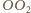 są równoległe. W takim razie odcinki
są równoległe. W takim razie odcinki 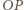 i
i 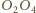 przecinają się w połowie jako przekątne równoległoboku.
przecinają się w połowie jako przekątne równoległoboku.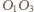 przechodzi przez środek odcinka
przechodzi przez środek odcinka 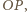 co daje tezę.
co daje tezę.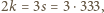 co jest niemożliwe.
co jest niemożliwe.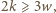 wielościan o 7 krawędziach miałby najwyżej 4 wierzchołki, a więc najwyżej 6 krawędzi - sprzeczność.
wielościan o 7 krawędziach miałby najwyżej 4 wierzchołki, a więc najwyżej 6 krawędzi - sprzeczność. krawędzi oraz płaszczyzna nie przechodząca przez żaden z jego wierzchołków i przecinająca
krawędzi oraz płaszczyzna nie przechodząca przez żaden z jego wierzchołków i przecinająca  krawędzi, przy czym
krawędzi, przy czym 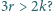
 krawędzi, to przekrój ma
krawędzi, to przekrój ma  boków i płaszczyzna ta przecina także
boków i płaszczyzna ta przecina także  różnych ścian (bo wielościan jest wypukły). Stąd
różnych ścian (bo wielościan jest wypukły). Stąd 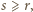 więc
więc 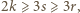 zatem niemożliwe, by
zatem niemożliwe, by 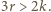
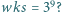
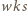 jest liczbą nieparzystą, to liczby
jest liczbą nieparzystą, to liczby 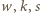 są nieparzyste, a więc niemożliwe, by
są nieparzyste, a więc niemożliwe, by 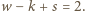
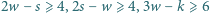 oraz
oraz 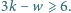
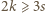 uzyskujemy
uzyskujemy 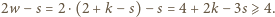 Pozostałych nierówności dowodzimy analogicznie.
Pozostałych nierówności dowodzimy analogicznie.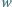 wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.
wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.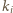 oznacza liczbę krawędzi ściany
oznacza liczbę krawędzi ściany 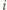 dla
dla 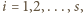 wówczas
wówczas 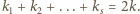 Suma kątów płaskich ścian wielościanu równa jest
Suma kątów płaskich ścian wielościanu równa jest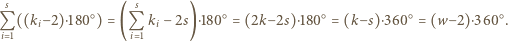
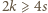 oraz
oraz 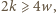 zatem
zatem 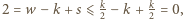 sprzeczność.
sprzeczność. liczbę ścian
liczbę ścian  -kątnych, a przez
-kątnych, a przez  liczbę naroży
liczbę naroży 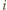 -ściennych
-ściennych 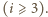
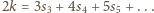 oraz
oraz 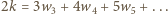 Stąd
Stąd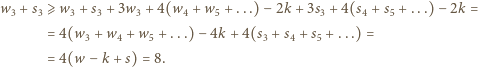
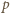 ścian pięciokątnych i
ścian pięciokątnych i 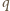 sześciokątnych, to
sześciokątnych, to 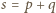 oraz
oraz 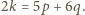 Wielokąty są foremne, zatem w każdym wierzchołku schodzą się po trzy. Stąd
Wielokąty są foremne, zatem w każdym wierzchołku schodzą się po trzy. Stąd 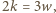 czyli
czyli 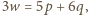 a więc
a więc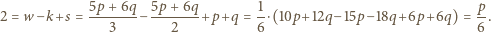
 - wielościan ma 12 ścian pięciokątnych.
- wielościan ma 12 ścian pięciokątnych.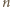 -kątów foremnych, po
-kątów foremnych, po 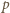 w każdym wierzchołku. Oznacza to, że
w każdym wierzchołku. Oznacza to, że 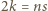 oraz
oraz 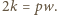 Wobec tego
Wobec tego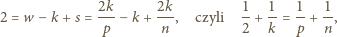
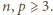 Równanie to ma pięć rozwiązań.
Równanie to ma pięć rozwiązań.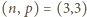 czworościan,
czworościan, 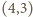 - sześcian,
- sześcian, 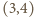 - ośmiościan,
- ośmiościan, 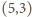 - dwunastościan i
- dwunastościan i 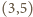 - dwudziestościan. Powyższe rozumowanie wskazuje, że więcej ich być nie może.
- dwudziestościan. Powyższe rozumowanie wskazuje, że więcej ich być nie może.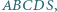 którego podstawą jest prostokąt
którego podstawą jest prostokąt 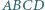 i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość
i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość 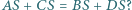 Odpowiedź uzasadnij.
Odpowiedź uzasadnij.