Zadanie ZM-1465
o zadaniu...
- Publikacja w Delcie: sierpień 2015
- Publikacja elektroniczna: 31-07-2015
Czy istnieje przekrój dwudziestościanu foremnego płaszczyzną przechodzącą przez jego środek, będący jedenastokątem?
Czy istnieje przekrój dwudziestościanu foremnego płaszczyzną przechodzącą przez jego środek, będący jedenastokątem?
Rys. 1a
Rys. 1a
Proszę ocenić poprawność poniższego stwierdzenia.
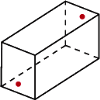
Pokój ma kształt prostopadłościanu o wymiarach 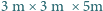 (Rys. 1a). Nad środkiem jednej z krótszych krawędzi podłogi, na wysokości
(Rys. 1a). Nad środkiem jednej z krótszych krawędzi podłogi, na wysokości 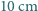 , siedzi pająk. Chce on dotrzeć do punktu położonego
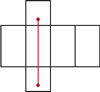
, siedzi pająk. Chce on dotrzeć do punktu położonego 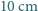 pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na rysunku 1b.
pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na rysunku 1b.

Proszę ocenić poprawność poniższego rozumowania.
Dany jest ostrosłup prawidłowy o krawędzi bocznej długości 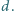 W wierzchołku
W wierzchołku 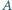 podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż
podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż 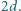
Czy istnieje wielościan wypukły, którego dokładnie jedna ściana nie jest wielokątem foremnym?
Czy istnieje taki ostrosłup czworokątny, którego każda ściana boczna jest trójkątem prostokątnym?
Czy istnieje taki wielościan wypukły, który ma nieparzystą liczbę krawędzi i którego każda ściana ma parzystą liczbę boków?
Czy istnieje wielościan wypukły mający dokładnie 100 ścian, z których co najmniej jedna jest 99-kątem i taki, że w każdym jego wierzchołku zbiegają się dokładnie trzy krawędzie?
Czy istnieje taki wielościan wypukły, że w każdym jego wierzchołku schodzą się co najmniej cztery krawędzie, i który można przeciąć pewną płaszczyzną, otrzymując w przekroju trójkąt?
Czy istnieje taki wielościan wypukły, który ma nieparzystą liczbę ścian, i w którego każdym wierzchołku schodzi się parzysta liczba krawędzi?
Zadanie 688 zaproponował pan Witold Bednarek z Łodzi.
Trójkąt równoboczny 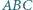 o boku długości 1 jest podstawą ostrosłupa prawidłowego
o boku długości 1 jest podstawą ostrosłupa prawidłowego 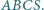 Na krawędziach
Na krawędziach 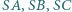 leżą takie punkty
leżą takie punkty 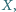
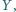
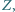 że suma kwadratów pól trójkątów
że suma kwadratów pól trójkątów  jest równa kwadratowi pola trójkąta
jest równa kwadratowi pola trójkąta 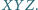 Obliczyć objętość ostrosłupa
Obliczyć objętość ostrosłupa 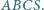
Czy istnieje taki ostrosłup czworokątny, że dwie jego ściany boczne nie mające wspólnej krawędzi są prostopadłe do podstawy?
Wszystkie ściany boczne pewnego ostrosłupa o podstawie kwadratowej są trójkątami równoramiennymi. Czy ostrosłup ten musi być prawidłowy?
Czy istnieje czworościan, którego każda ściana jest trójkątem rozwartokątnym?
Czy wysokości czworościanu muszą przecinać się w jednym punkcie?
Czy istnieje wielościan wypukły, w którym można tak wybrać ponad połowę jego ścian, aby żadne dwie z wybranych ścian nie miały wspólnej krawędzi?
Czy każdy wielościan można striangulować, czyli podzielić na czworościany o wierzchołkach w wierzchołkach wyjściowego wielościanu?
Czy istnieje taki czworościan, w którym spodek żadnej wysokości nie należy do odpowiadającej jej podstawy?
Czy istnieje ostrosłup o podstawie będącej czworokątem wklęsłym, którego dwie ściany boczne nie mające wspólnej krawędzi są prostopadłe do podstawy?
Czy istnieje taki ostrosłup czworokątny oraz taka płaszczyzna przecinająca wszystkie jego krawędzie boczne, że pole uzyskanego przekroju jest większe od pola podstawy ostrosłupa?