Topologia na Antypodach
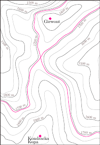
Mapa obok przedstawia rejon Giewontu i Kopy Kondrackiej. Typowa poziomica jest albo pusta (np. nie ma żadnych punktów na wysokości 2500 m), albo składa się z jednej lub więcej składowych, z których każda jest albo zamkniętą pętlą (jak ta wokół Giewontu, 1800 m), albo krzywą o dwóch końcach na brzegu mapy (np. te powyżej dolin Małej Łąki i Kondratowej, 1600 m). Może się jednak zdarzyć, że poziomica jest osobliwa - na wysokości 1894 m mamy izolowany punkt (szczyt Giewontu), a na 1725 m przecięcie w kształcie litery X (Kondracka Przełęcz). Są to jednak pojedyncze przypadki - jak szczyt, przełęcz albo dno kotła - a wszystkie pozostałe poziomice są regularne.

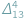 w artykule Złośliwy problem
w artykule Złośliwy problem  i kubełkowe struktury danych...
i kubełkowe struktury danych... zaproponował czytelnikom Journal of the Indian Mathematical Society (JIMS 3 (1911), Question 289, p. 90) wyznaczenie wartości: (a)
zaproponował czytelnikom Journal of the Indian Mathematical Society (JIMS 3 (1911), Question 289, p. 90) wyznaczenie wartości: (a) 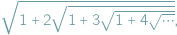 (b)
(b)  Ponieważ pytania te w 1911 r. nie doczekały się odpowiedzi, więc Ramanujan podał je w kolejnym tomie JIMS 4 (1912), p. 226. Zadania Ramanujana można rozwiązać prosto i elegancko.
Ponieważ pytania te w 1911 r. nie doczekały się odpowiedzi, więc Ramanujan podał je w kolejnym tomie JIMS 4 (1912), p. 226. Zadania Ramanujana można rozwiązać prosto i elegancko.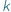 -elementowych podzbiorów zbioru
-elementowych podzbiorów zbioru 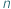 -elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez
-elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez 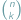 (symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
(symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...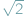 jest niewymierne, czyli że dla żadnej liczby naturalnej
jest niewymierne, czyli że dla żadnej liczby naturalnej 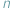 liczba
liczba 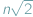 nie jest całkowita.
nie jest całkowita.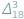 (Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
(Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
