Klub 44M - zadania IX 2018»Zadanie 765
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2018
- Publikacja w Delcie: wrzesień 2018
- Publikacja elektroniczna: 1 września 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (57 KB)
Czworokąt 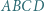 jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek
jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek 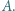 Zakładamy, że proste
Zakładamy, że proste 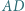 i
i 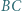 przecinają się w punkcie
przecinają się w punkcie 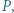 zaś proste
zaś proste 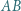 i
i 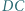 przecinają się w punkcie
przecinają się w punkcie 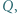 przy czym
przy czym 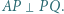 Niech
Niech 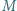 będzie środkiem przekątnej
będzie środkiem przekątnej 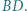 Wykazać, że
Wykazać, że 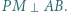

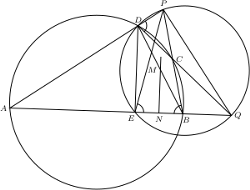
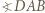 jest najmniejszym kątem czworokąta
jest najmniejszym kątem czworokąta 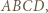 nietrudno wywnioskować, że punkt
nietrudno wywnioskować, że punkt 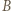 leży między
leży między 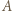 i
i 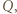 a punkt
a punkt 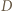 między
między 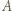 i
i 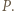 Weźmy pod uwagę okrąg o średnicy
Weźmy pod uwagę okrąg o średnicy 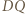 ; ów okrąg przechodzi przez punkt
; ów okrąg przechodzi przez punkt 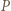 (bo
(bo 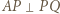 ) oraz przecina odcinek
) oraz przecina odcinek 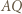 w punkcie, który nazwiemy
w punkcie, który nazwiemy 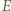 ; zatem
; zatem 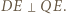
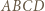 i
i 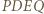 ma okrąg opisany. Wynikają stąd równości kątów
ma okrąg opisany. Wynikają stąd równości kątów 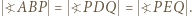 Zatem trójkąt
Zatem trójkąt 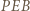 jest równoramienny.
jest równoramienny.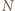 będzie środkiem odcinka
będzie środkiem odcinka 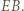 Skoro
Skoro 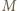 jest środkiem odcinka
jest środkiem odcinka 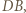 prosta
prosta 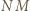 jest równoległa do prostej
jest równoległa do prostej 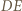 - która jest prostopadła do
- która jest prostopadła do 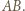 To znaczy, że prosta
To znaczy, że prosta 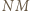 jest symetralną podstawy
jest symetralną podstawy 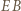 trójkąta równoramiennego
trójkąta równoramiennego 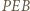 ; przechodzi więc przez punkt
; przechodzi więc przez punkt 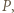 i mamy tezę
i mamy tezę