Zadanie ZM-1577
o zadaniu...
- Publikacja w Delcie: wrzesień 2018
- Publikacja elektroniczna: 1 września 2018
Rozważamy trójkąt równoboczny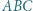 
o boku 
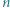podzielony na 
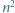trójkątów równobocznych o boku 
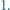Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 
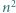trójkątów, nazwijmy węzłem.
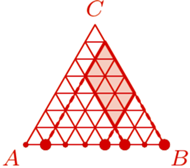
Wyznaczyć liczbę równoległoboków o wierzchołkach w węzłach, których dwa boki są równoległe do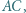 
a dwa do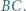 
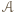będzie zbiorem 
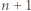węzłów należących do boku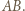 
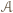jednoznacznie wyznacza równoległobok o zadanych własnościach, którego punktami przecięcia z 
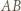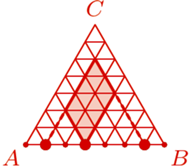
są te cztery punkty i którego "najniższy" wierzchołek nie leży na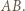 
Z kolei każda trójka różnych punktów z 
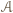jednoznacznie wyznacza taki równoległobok, którego "najniższy" wierzchołek leży na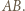 
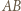w trzech lub czterech punktach i są to punkty należące do 
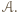Stąd wniosek, że szukana liczba równoległoboków jest równa łącznej liczbie wyborów trzech lub czterech elementów zbioru 
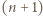-elementowego, czyli