Zadanie ZM-1578
o zadaniu...
- Publikacja w Delcie: wrzesień 2018
- Publikacja elektroniczna: 1 września 2018
Rozważamy trójkąt równoboczny 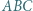 o boku
o boku 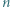 podzielony na
podzielony na 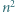 trójkątów równobocznych o boku
trójkątów równobocznych o boku  Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 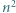 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.
Wyznaczyć liczbę trójkątów równobocznych o wierzchołkach w węzłach (ale bokach niekoniecznie równoległych do boków 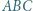 ).
).

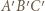 o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli
o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli 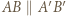 oraz punkty
oraz punkty 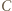 i
i 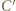 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 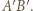
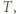 spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli
spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli 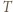 jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do
jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do 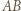 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 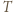 leżący najbliżej
leżący najbliżej 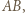 równoległą do
równoległą do 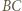 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 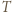 leżący najbliżej
leżący najbliżej 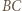 oraz równoległą do
oraz równoległą do 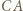 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 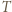 leżący najbliżej
leżący najbliżej 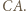
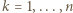 zostało w ten sposób przyporządkowanych dokładnie
zostało w ten sposób przyporządkowanych dokładnie 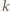 trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku
trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku 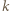 jest równa
jest równa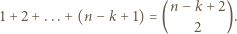
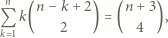
 którego drugim co do wielkości elementem jest
którego drugim co do wielkości elementem jest 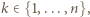 można wybrać na dokładnie
można wybrać na dokładnie 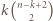 sposobów (wybierając najmniejszy element spośród
sposobów (wybierając najmniejszy element spośród 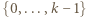 oraz dwa większe od
oraz dwa większe od 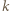 spośród
spośród 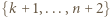 ). Sumując po wszystkich możliwych
). Sumując po wszystkich możliwych 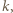 uzyskujemy liczbę sposobów wyboru
uzyskujemy liczbę sposobów wyboru 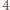 spośród
spośród 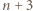 elementów.
elementów.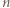 ) oraz w poprzednim (dla trójkąta o boku
) oraz w poprzednim (dla trójkąta o boku 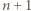 ).
).