Nigdy Cię nie zobaczę?
- Hop, hop, jest tam kto? - krzyczy 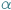 otoczona tłumem.
otoczona tłumem.
- Hop, hop, spójrz tutaj. - odpowiada 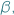 który co prawda słyszy
który co prawda słyszy 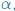 ale zupełnie jej nie widzi.
ale zupełnie jej nie widzi.
- Jakie "tutaj"? Przecież dookoła nie ma żywej duszy. - 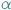 otoczona tłumem po raz kolejny usiłuje dostrzec
otoczona tłumem po raz kolejny usiłuje dostrzec 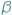 pośród otaczającej pustki.
pośród otaczającej pustki.
Dookoła ludzi tłum, a jakby nikogo nie było  Przyjrzyjmy się światu, w którym
Przyjrzyjmy się światu, w którym 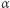 i
i 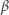 próbują się bezskutecznie dostrzec. Na zwykłej płaszczyźnie
próbują się bezskutecznie dostrzec. Na zwykłej płaszczyźnie
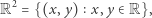 |
w każdym jej punkcie o wymiernych współrzędnych 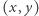 siedzi samotny człowiek i... wypatruje towarzysza, kierując tęsknie wzrok w losowo obranym kierunku. Ten losowy kierunek jest wyznaczony przez wybór punktu na ruletce o promieniu 1 - zadekretowane prawdopodobieństwo wylosowania półprostej wzroku przebijającej brzeg ruletki na łuku
siedzi samotny człowiek i... wypatruje towarzysza, kierując tęsknie wzrok w losowo obranym kierunku. Ten losowy kierunek jest wyznaczony przez wybór punktu na ruletce o promieniu 1 - zadekretowane prawdopodobieństwo wylosowania półprostej wzroku przebijającej brzeg ruletki na łuku 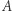 wynosi
wynosi ![[A]/2 |](/math/temat/matematyka/rachunek_prawdopodobienstwa/2020/11/30/nigdy-cie-nie-zobacze/7x-231ebcfda85e4e2e3778d897ae154bc46cf06426-im-33,33,33-FF,FF,FF.gif) (
( ![[A] |](/math/temat/matematyka/rachunek_prawdopodobienstwa/2020/11/30/nigdy-cie-nie-zobacze/8x-231ebcfda85e4e2e3778d897ae154bc46cf06426-im-33,33,33-FF,FF,FF.gif) oznacza długość łuku
oznacza długość łuku 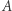 ). Oczywiście każdy ma swoją osobistą ruletkę i każdy wykręca kierunek swojego spojrzenia niezależnie.
). Oczywiście każdy ma swoją osobistą ruletkę i każdy wykręca kierunek swojego spojrzenia niezależnie.
Dla 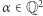 niech
niech 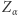 oznacza zdarzenie, że
oznacza zdarzenie, że 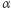 kogoś widzi. Wykażemy, że
kogoś widzi. Wykażemy, że 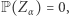 niestety... Zauważmy, że moc zbioru prostych
niestety... Zauważmy, że moc zbioru prostych 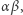 gdzie
gdzie 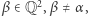 jest nie większa niż moc zbioru punktów
jest nie większa niż moc zbioru punktów 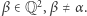 Oznacza to, że moc zbioru tych prostych jest przeliczalna - stąd teza.
Oznacza to, że moc zbioru tych prostych jest przeliczalna - stąd teza.

Ale nie tylko 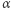 nikogo nie widzi. Ponieważ miara probabilistyczna jest przeliczalnie addytywna, więc również
nikogo nie widzi. Ponieważ miara probabilistyczna jest przeliczalnie addytywna, więc również
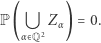 |
Zatem zdarzenie przeciwne jest pewne
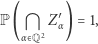 |
czyli prawie na pewno nikt nikogo nie widzi. Zauważmy, że założenie o niezależności rozglądania się różnych osób jest w zasadzie zbędne.
No dobrze... Wiemy skądinąd, że zdarzenie niemożliwe może się zdarzyć. Wyobraźmy sobie, że jakimś cudem 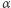 spojrzała w przestrzeń tak, że zobaczyła swoją drugą połówkę, którą jest
spojrzała w przestrzeń tak, że zobaczyła swoją drugą połówkę, którą jest 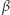 (oczywiście
(oczywiście 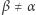 ). Mimo cudu nie zdołają się zobaczyć! Na drodze między
). Mimo cudu nie zdołają się zobaczyć! Na drodze między 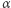 i
i 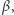 dokładnie w połowie, stoi bowiem
dokładnie w połowie, stoi bowiem 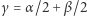 (rzecz jasna
(rzecz jasna 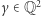 ). Oznacza to, że
). Oznacza to, że 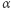 nie widzi
nie widzi 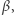 ponieważ jest zasłonięty przez
ponieważ jest zasłonięty przez 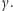 Oczywiście z podobnych powodów
Oczywiście z podobnych powodów 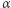 nie widzi
nie widzi 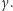 Idąc dalej tym tropem, dochodzimy do wniosku, że na pewno (bez wyjątków i cudów) nikt nie widzi nikogo (bez żadnego modelu probabilistycznego!).
Idąc dalej tym tropem, dochodzimy do wniosku, że na pewno (bez wyjątków i cudów) nikt nie widzi nikogo (bez żadnego modelu probabilistycznego!).
Hmm... Coś jest nie tak w naszym świecie - po prostu ludzie siedzą za gęsto i to prowadzi do powyższych paradoksów interpretacyjnych. Zmieńmy ten świat na lepszy! Usadowmy ludzi wyłącznie w punktach kraty całkowitoliczbowej 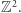 Oczywiście wcześniejszy model probabilistyczny znowu jest użyteczny i daje pewien wgląd w beznadziejną sytuację ludzkości:nikt nie dostrzega innych, prawie na pewno.
Oczywiście wcześniejszy model probabilistyczny znowu jest użyteczny i daje pewien wgląd w beznadziejną sytuację ludzkości:nikt nie dostrzega innych, prawie na pewno.
Pojawia się jednak naturalne pytanie o prawdopodobieństwo zdarzenia, że losowo sobie przeznaczeni 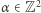 oraz
oraz 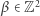 mogą się zobaczyć, jeśli spojrzą we właściwym kierunku. Niech zatem
mogą się zobaczyć, jeśli spojrzą we właściwym kierunku. Niech zatem 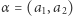 oraz
oraz 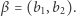 Łatwo, nomen omen, widzieć, że
Łatwo, nomen omen, widzieć, że 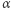 i
i 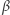 mogą się zobaczyć wtedy i tylko wtedy, gdy nikt nie stoi im na drodze, czyli
mogą się zobaczyć wtedy i tylko wtedy, gdy nikt nie stoi im na drodze, czyli 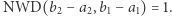 Dowodzi się w teorii liczb, że
Dowodzi się w teorii liczb, że
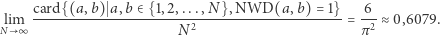 |
Oto szkic rozumowania prowadzącego do tego intrygującego wyniku. Niech 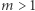 będzie dowolną, ale ustaloną liczbą naturalną. Jakie jest prawdopodobieństwo, że losując spośród liczb naturalnych, otrzymamy taką, która będzie podzielna przez
będzie dowolną, ale ustaloną liczbą naturalną. Jakie jest prawdopodobieństwo, że losując spośród liczb naturalnych, otrzymamy taką, która będzie podzielna przez 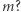 Intuicja podpowiada, że
Intuicja podpowiada, że 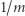 : jeśli losujemy tę liczbę ze zbioru
: jeśli losujemy tę liczbę ze zbioru 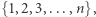 i wylosowanie każdej liczby jest jednakowo prawdopodobne, to prawdopodobieństwo
i wylosowanie każdej liczby jest jednakowo prawdopodobne, to prawdopodobieństwo 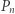 rozważanego zdarzenia wynosi dokładnie
rozważanego zdarzenia wynosi dokładnie
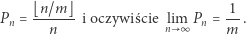 |

Należy więc uznać (można to łatwo sformalizować), iż prawdopodobieństwo zdarzenia 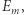 że dwie niezależnie wylosowane liczby całkowite
że dwie niezależnie wylosowane liczby całkowite 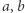 są obie podzielne przez
są obie podzielne przez 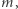 wynosi
wynosi 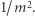 Prawdopodobieństwo zdarzenia przeciwnego
Prawdopodobieństwo zdarzenia przeciwnego 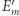 wynosi zatem
wynosi zatem 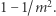 Niech teraz
Niech teraz
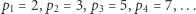 |
będzie ciągiem rosnącym wszystkich liczb pierwszych. Zauważmy, że 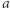 i
i 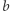 są względnie pierwsze wtedy i tylko wtedy, gdy nie są podzielne równocześnie przez żadną liczbę pierwszą
są względnie pierwsze wtedy i tylko wtedy, gdy nie są podzielne równocześnie przez żadną liczbę pierwszą 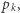 czyli gdy zajdzie zdarzenie
czyli gdy zajdzie zdarzenie 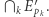 Przyda się teraz obserwacja, że jeśli
Przyda się teraz obserwacja, że jeśli 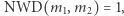 to zdarzenia
to zdarzenia 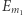 oraz
oraz 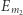 są niezależne - wynika to stąd, że liczba całkowita dzieli się jednocześnie przez
są niezależne - wynika to stąd, że liczba całkowita dzieli się jednocześnie przez 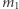 oraz
oraz 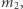 gdy dzieli się przez
gdy dzieli się przez 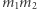 oraz ze wzoru
oraz ze wzoru 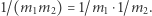 Uogólniając tę obserwację, widzimy, że zarówno
Uogólniając tę obserwację, widzimy, że zarówno 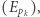 jak i
jak i 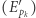 są ciągami zdarzeń niezależnych. W szczególności zachodzi
są ciągami zdarzeń niezależnych. W szczególności zachodzi
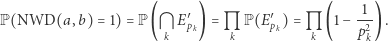 |
Już Leonhard Euler zauważył, że dla 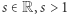 mamy
mamy
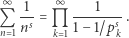 |
Formalnie ta tożsamość wynika ze wzoru na sumę ciągu geometrycznego
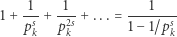 |
i twierdzenia o jednoznacznym rozkładzie każdej liczby naturalnej na iloczyn potęg liczb pierwszych. Wyżej występujące szeregi i iloczyny nieskończone są rzeczywiście zbieżne, ale mówi się, że Euler specjalnie tym się nie przejmował. Geniusz Eulera przejawił się jednak szczególnie wtedy, gdy obwieścił światu, że
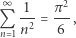 |
i przedstawił wyprowadzenie tego wyniku. Jak na dzisiejsze standardy ścisłości matematycznej jego uzasadnienie nie było do końca zadowalające, ale w zasadzie poprawne. To, że powyższy szereg, tylko niewinnie różniący się od szeregu
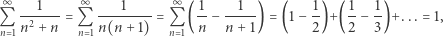 |
ma tak intrygującą sumę, zakrawa na cud! Naszkicowaliśmy zatem dowód faktu, że przeznaczeni sobie mają więcej niż 3 szanse na 5, że nikt im nie stanie na przeszkodzie.