Deltoid
Prawdopodobieństwo geometryczne
Rozmaite zagadnienia można wygodnie i ładnie ilustrować geometrycznie. Jeśli wyniki doświadczenia losowego dają się zinterpretować jako punkty pewnego obszaru i każdy wynik jest jednakowo prawdopodobny, to prawdopodobieństwo określonego zdarzenia można wyznaczyć jako stosunek miary (pola, objętości etc.) odpowiadającej mu części obszaru do miary całości.
Słynnym przykładem jest tzw. igła Buffona, z którą związana jest ciekawa metoda eksperymentalnego przybliżania wartości liczby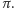 
Więcej na ten temat w artykule Regularność przypadku w tym numerze Delty.
Trzeba jednak uważać na pewne trudności, widoczne np. w paradoksie Bertranda, w którym na to samo pytanie udziela się trzech różnych odpowiedzi. Można o nim przeczytać np. w artykule Paradoksy rachunku prawdopodobieństwa w Delcie nr 4/1992.