Każdy ruch zmniejsza wartość przekazywanej liczby. Gra się zatem zawsze
kończy, a któryś z graczy ma strategię wygrywającą. Dodatnią liczbę
całkowitą nazwijmy zieloną, jeśli – startując od tej liczby – gracz rozpoczynający
ma strategię zwycięską; nazwijmy ją czerwoną, gdy strategię zwycięską ma jego
przeciwnik; również liczbę 0 będziemy uważać za czerwoną. Wykażemy,
że liczba
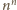 jest zielona; a więc (jak zwykle w tego typu zadaniach)
wygrywa dziewczyna.
jest zielona; a więc (jak zwykle w tego typu zadaniach)
wygrywa dziewczyna.
Rozbicie zbioru liczb całkowitych nieujemnych na liczby zielone i czerwone jest
scharakteryzowane przez własności:
-
(1)
- od każdej liczby zielonej można przejść jednym ruchem do
czerwonej;
-
(2)
- od każdej liczby czerwonej wszystkie ruchy prowadzą do liczb
zielonych.
Wśród liczb mniejszych od
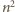 liczbami czerwonymi są wielokrotności
liczby
liczbami czerwonymi są wielokrotności
liczby
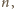 i tylko one; sprawdzenie własności (1), (2) jest natychmiastowe.
Sama liczba
i tylko one; sprawdzenie własności (1), (2) jest natychmiastowe.
Sama liczba
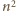 jest wszelako zielona (dzielenie przez
jest wszelako zielona (dzielenie przez
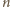 prowadzi do
czerwonej liczby
prowadzi do
czerwonej liczby
 ). Liczby z przedziału
). Liczby z przedziału
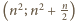 też są
zielone (dzielenie z zaokrągleniem prowadzi do
też są
zielone (dzielenie z zaokrągleniem prowadzi do
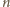 ). Zajmiemy się teraz
liczbami większymi.
). Zajmiemy się teraz
liczbami większymi.
Przyjmijmy
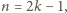 czyli
czyli
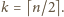 Weźmy pod uwagę
zbiór
Weźmy pod uwagę
zbiór
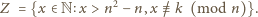
Udowodnimy, że wszystkie liczby w zbiorze
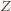 są zielone.
są zielone.
Przypuśćmy, że tak nie jest. Niech
 będzie najmniejszą liczbą
czerwoną w zbiorze
będzie najmniejszą liczbą
czerwoną w zbiorze
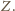 Wiemy już, że zielone są wszystkie liczby od
Wiemy już, że zielone są wszystkie liczby od
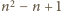 do
do
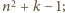 tak więc
tak więc
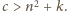 Niech
Niech
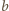 będzie największą liczbą spełniającą warunki
będzie największą liczbą spełniającą warunki
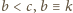 (mod
(mod
 ); zatem
); zatem
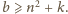 Jest ona osiągalna z liczby
Jest ona osiągalna z liczby
 ruchem
odejmowania.
ruchem
odejmowania.
Dzielenie przez
 z zaokrągleniem, zastosowane do każdej z liczb
z zaokrągleniem, zastosowane do każdej z liczb
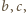 daje w wyniku tę samą liczbę
daje w wyniku tę samą liczbę
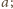 konkretnie: liczbę
konkretnie: liczbę
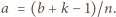 Liczba
Liczba
 jest czerwona, więc w myśl
własności (2) liczby
jest czerwona, więc w myśl
własności (2) liczby
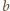 i
i
 (osiągalne z
(osiągalne z
 ) są zielone.
W myśl własności (1), istnieje ruch, prowadzący od liczby
) są zielone.
W myśl własności (1), istnieje ruch, prowadzący od liczby
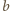 do jakiejś
liczby czerwonej. Nie jest to dzielenie z zaokrągleniem (które daje liczbę
do jakiejś
liczby czerwonej. Nie jest to dzielenie z zaokrągleniem (które daje liczbę
 ); zaś odejmowanie od
); zaś odejmowanie od
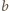 liczb
liczb
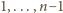 nie
wyprowadza ze zbioru
nie
wyprowadza ze zbioru
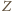 (skoro
(skoro
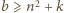 oraz
oraz
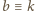 ).
Któraś z tak uzyskanych różnic powinna być liczbą czerwoną –
wbrew określeniu
).
Któraś z tak uzyskanych różnic powinna być liczbą czerwoną –
wbrew określeniu
 jako najmniejszej liczby czerwonej w zbiorze
jako najmniejszej liczby czerwonej w zbiorze
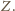
Sprzeczność dowodzi, że istotnie cały zbiór
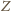 jest zielony.
Oczywiście
jest zielony.
Oczywiście
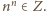 Ala wygrywa.
Ala wygrywa.
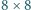 ułożono 12 klocków o wymiarach
ułożono 12 klocków o wymiarach
 tak,
aby każdy klocek pokrywał całkowicie 5 pól. Które cztery pola pozostały
niepokryte?
tak,
aby każdy klocek pokrywał całkowicie 5 pól. Które cztery pola pozostały
niepokryte?
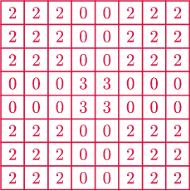
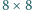 stoi królowa. Gracze na przemian
przesuwają ją o dowolną liczbę pól w prawo, do góry albo po przekątnej
w prawo i do góry. Wygrywa ten, kto postawi królową na polu h8. Który
gracz ma strategię wygrywającą i jaką?
stoi królowa. Gracze na przemian
przesuwają ją o dowolną liczbę pól w prawo, do góry albo po przekątnej
w prawo i do góry. Wygrywa ten, kto postawi królową na polu h8. Który
gracz ma strategię wygrywającą i jaką?
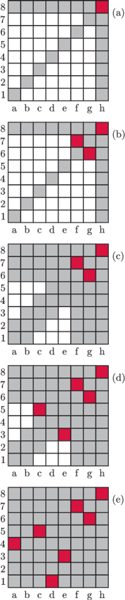
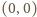 (nic jeszcze nie
zjedzono) odpowiada początkowemu polu c1. Wygrywa ten, kto zje ostatni
owoc, czyli zajmie pozycję
(nic jeszcze nie
zjedzono) odpowiada początkowemu polu c1. Wygrywa ten, kto zje ostatni
owoc, czyli zajmie pozycję
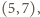 odpowiadającą polu h8. Po takim
„przetłumaczeniu” problemu można natychmiast wywnioskować z zadania 1,
że strategię wygrywającą ma gracz rozpoczynający (i nawet wiemy,
jaką!)
odpowiadającą polu h8. Po takim
„przetłumaczeniu” problemu można natychmiast wywnioskować z zadania 1,
że strategię wygrywającą ma gracz rozpoczynający (i nawet wiemy,
jaką!)
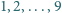 napisano na osobnych kartkach. Gracze na przemian
zabierają sobie po jednej z nich. Wygrywa ten, kto jako pierwszy skompletuje
trzy kartki o sumie liczb równej 15. Gracz rozpoczynający wybrał kartkę z „2”.
Jak powinien postąpić drugi gracz?
napisano na osobnych kartkach. Gracze na przemian
zabierają sobie po jednej z nich. Wygrywa ten, kto jako pierwszy skompletuje
trzy kartki o sumie liczb równej 15. Gracz rozpoczynający wybrał kartkę z „2”.
Jak powinien postąpić drugi gracz?
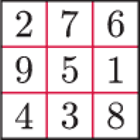
 Ala i Bartek grają w grę,
wykonując ruchy na przemian. Stan gry jest liczbą całkowitą i zmienia swą
wartość w trakcie gry. Gracz, do którego należy ruch, może do tej
liczby zastosować jedną z dwóch operacji: odjąć od niej dowolną
dodatnią liczbę całkowitą, mniejszą niż
Ala i Bartek grają w grę,
wykonując ruchy na przemian. Stan gry jest liczbą całkowitą i zmienia swą
wartość w trakcie gry. Gracz, do którego należy ruch, może do tej
liczby zastosować jedną z dwóch operacji: odjąć od niej dowolną
dodatnią liczbę całkowitą, mniejszą niż
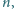 albo podzielić ją przez
albo podzielić ją przez
 i zaokrąglić wynik do najbliższej liczby całkowitej (wobec
nieparzystości
i zaokrąglić wynik do najbliższej liczby całkowitej (wobec
nieparzystości
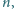 kierunek zaokrąglenia jest zawsze dobrze określony).
Powstała nowa wartość przechodzi do dyspozycji przeciwnika. Wygrywa,
kto pierwszy uzyska wartość 0. Rozpoczyna Ala, startując od liczby
kierunek zaokrąglenia jest zawsze dobrze określony).
Powstała nowa wartość przechodzi do dyspozycji przeciwnika. Wygrywa,
kto pierwszy uzyska wartość 0. Rozpoczyna Ala, startując od liczby
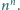 Kto ma strategię wygrywającą?
Kto ma strategię wygrywającą?
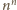 jest zielona; a więc (jak zwykle w tego typu zadaniach)
wygrywa dziewczyna.
jest zielona; a więc (jak zwykle w tego typu zadaniach)
wygrywa dziewczyna.
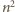 liczbami czerwonymi są wielokrotności
liczby
liczbami czerwonymi są wielokrotności
liczby
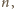 i tylko one; sprawdzenie własności (1), (2) jest natychmiastowe.
Sama liczba
i tylko one; sprawdzenie własności (1), (2) jest natychmiastowe.
Sama liczba
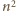 jest wszelako zielona (dzielenie przez
jest wszelako zielona (dzielenie przez
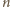 prowadzi do
czerwonej liczby
prowadzi do
czerwonej liczby
 ). Liczby z przedziału
). Liczby z przedziału
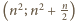 też są
zielone (dzielenie z zaokrągleniem prowadzi do
też są
zielone (dzielenie z zaokrągleniem prowadzi do
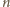 ). Zajmiemy się teraz
liczbami większymi.
). Zajmiemy się teraz
liczbami większymi.
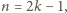 czyli
czyli
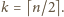 Weźmy pod uwagę
zbiór
Weźmy pod uwagę
zbiór
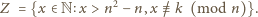
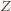 są zielone.
są zielone.
 będzie najmniejszą liczbą
czerwoną w zbiorze
będzie najmniejszą liczbą
czerwoną w zbiorze
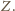 Wiemy już, że zielone są wszystkie liczby od
Wiemy już, że zielone są wszystkie liczby od
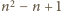 do
do
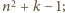 tak więc
tak więc
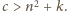 Niech
Niech
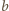 będzie największą liczbą spełniającą warunki
będzie największą liczbą spełniającą warunki
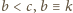 (mod
(mod
 ); zatem
); zatem
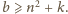 Jest ona osiągalna z liczby
Jest ona osiągalna z liczby
 ruchem
odejmowania.
ruchem
odejmowania.
 z zaokrągleniem, zastosowane do każdej z liczb
z zaokrągleniem, zastosowane do każdej z liczb
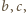 daje w wyniku tę samą liczbę
daje w wyniku tę samą liczbę
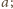 konkretnie: liczbę
konkretnie: liczbę
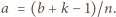 Liczba
Liczba
 jest czerwona, więc w myśl
własności (2) liczby
jest czerwona, więc w myśl
własności (2) liczby
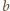 i
i
 (osiągalne z
(osiągalne z
 ) są zielone.
W myśl własności (1), istnieje ruch, prowadzący od liczby
) są zielone.
W myśl własności (1), istnieje ruch, prowadzący od liczby
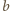 do jakiejś
liczby czerwonej. Nie jest to dzielenie z zaokrągleniem (które daje liczbę
do jakiejś
liczby czerwonej. Nie jest to dzielenie z zaokrągleniem (które daje liczbę
 ); zaś odejmowanie od
); zaś odejmowanie od
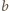 liczb
liczb
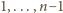 nie
wyprowadza ze zbioru
nie
wyprowadza ze zbioru
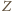 (skoro
(skoro
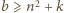 oraz
oraz
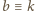 ).
Któraś z tak uzyskanych różnic powinna być liczbą czerwoną –
wbrew określeniu
).
Któraś z tak uzyskanych różnic powinna być liczbą czerwoną –
wbrew określeniu
 jako najmniejszej liczby czerwonej w zbiorze
jako najmniejszej liczby czerwonej w zbiorze
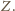
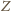 jest zielony.
Oczywiście
jest zielony.
Oczywiście
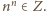 Ala wygrywa.
Ala wygrywa.

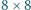 , jedna kostka jest zatruta (
, jedna kostka jest zatruta (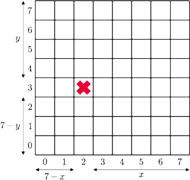
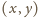 jest zatrute. Pokażemy, że Lolek ma
strategię wygrywającą. Gra polega tak naprawdę na zmniejszaniu przez graczy
w każdym ruchu jednej z liczb
jest zatrute. Pokażemy, że Lolek ma
strategię wygrywającą. Gra polega tak naprawdę na zmniejszaniu przez graczy
w każdym ruchu jednej z liczb
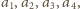 które na początku mają
wartości
które na początku mają
wartości
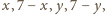 odpowiednio, a oznaczają liczbę kolumn na
prawo, na lewo, liczbę wierszy w górę, w dół od zatrutego pola w aktualnej
tabliczce czekolady. Rozważmy liczbę
odpowiednio, a oznaczają liczbę kolumn na
prawo, na lewo, liczbę wierszy w górę, w dół od zatrutego pola w aktualnej
tabliczce czekolady. Rozważmy liczbę
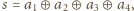 gdzie
gdzie
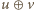 oznacza dodawanie liczb
oznacza dodawanie liczb
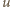 i
i
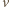 zapisanych binarnie,
bez przeniesienia (np.
zapisanych binarnie,
bez przeniesienia (np.
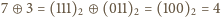 ).
).
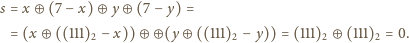
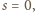 w następnym ruchu będziemy mieli
w następnym ruchu będziemy mieli
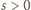 (któraś z liczb
(któraś z liczb
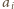 zmieniła się). Gdy
zmieniła się). Gdy
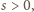 zawsze
istnieje taki ruch, że po jego wykonaniu
zawsze
istnieje taki ruch, że po jego wykonaniu
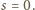 Istotnie, bez utraty
ogólności możemy zakładać, że
Istotnie, bez utraty
ogólności możemy zakładać, że
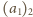 ma niezerowy bit na pozycji
pierwszego bitu znaczącego liczby
ma niezerowy bit na pozycji
pierwszego bitu znaczącego liczby
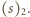 Wówczas
Wówczas
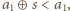 więc
wystarczy zmniejszyć liczbę
więc
wystarczy zmniejszyć liczbę
 o
o
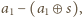 bo wtedy liczba
bo wtedy liczba
 wyniesie
wyniesie
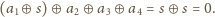
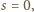 więc w końcu Bolek zastanie sytuację, w której
więc w końcu Bolek zastanie sytuację, w której
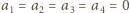 (w każdym ruchu któraś liczba się zmniejsza),
co odpowiada temu, że Bolek zostanie z zatrutą kostką i przegra.
(w każdym ruchu któraś liczba się zmniejsza),
co odpowiada temu, że Bolek zostanie z zatrutą kostką i przegra.
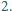 Wygrywa ten, który pierwszy przekroczy
Wygrywa ten, który pierwszy przekroczy
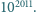 Który
z graczy ma strategię wygrywającą?
Który
z graczy ma strategię wygrywającą?
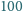 i z
i z
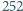 zapałkami. Dwóch graczy
na przemian zabiera z dowolnej kupki liczbę zapałek bedącą dzielnikiem liczby
zapałek w pozostałej kupce. Który z graczy ma strategię wygrywającą?
zapałkami. Dwóch graczy
na przemian zabiera z dowolnej kupki liczbę zapałek bedącą dzielnikiem liczby
zapałek w pozostałej kupce. Który z graczy ma strategię wygrywającą?
 zapałkami?
zapałkami?
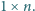 Na jej ostatnich
trzech polach stoi po jednym pionku. Dwóch graczy wykonuje naprzemiennie
ruchy polegające na przestawieniu dowolnego pionka na dowolne wolne pole
bliższe początku planszy. Przegrywa ten, który nie może zrobić ruchu.
Który z graczy ma strategię wygrywającą?
Na jej ostatnich
trzech polach stoi po jednym pionku. Dwóch graczy wykonuje naprzemiennie
ruchy polegające na przestawieniu dowolnego pionka na dowolne wolne pole
bliższe początku planszy. Przegrywa ten, który nie może zrobić ruchu.
Który z graczy ma strategię wygrywającą?
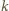 pionków stoi na końcowych polach planszy. Jeżeli zarówno
pionków stoi na końcowych polach planszy. Jeżeli zarówno
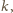 jak i
jak i
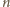 są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
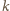 jest parzyste, a
jest parzyste, a
 nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
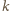 jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
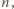 pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
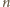 i
i
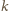 parzystych – a wiec
zawsze wygra.
parzystych – a wiec
zawsze wygra.
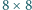 wieże,
tak by żadne dwie z nich się nie biły (wieża atakuje wszystkie pola
w swoim wierszu i w swojej kolumnie, gracze mają duży zapas wież).
Przegra ten z graczy, który jako pierwszy nie będzie mógł postawić
kolejnej wieży. Który gracz (rozpoczynający czy drugi) może zawsze
wygrać?
wieże,
tak by żadne dwie z nich się nie biły (wieża atakuje wszystkie pola
w swoim wierszu i w swojej kolumnie, gracze mają duży zapas wież).
Przegra ten z graczy, który jako pierwszy nie będzie mógł postawić
kolejnej wieży. Który gracz (rozpoczynający czy drugi) może zawsze
wygrać?
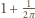 km (z pewną dokładnością). Chodzi o to, by potem, po
przebyciu kilometra, dojść w takie miejsce, skąd po kilometrowym
marszu na zachód znów się w nim znajdziemy. Ale są jeszcze inne
takie punkty! Można przecież, idąc na zachód, okrążyć biegun kilka
razy... Mimo to biegun północny jest jedynym rozwiązaniem, gdyż
na Antarktydzie nie ma niedźwiedzi. A niedźwiedź, oczywiście,
jest biały.
km (z pewną dokładnością). Chodzi o to, by potem, po
przebyciu kilometra, dojść w takie miejsce, skąd po kilometrowym
marszu na zachód znów się w nim znajdziemy. Ale są jeszcze inne
takie punkty! Można przecież, idąc na zachód, okrążyć biegun kilka
razy... Mimo to biegun północny jest jedynym rozwiązaniem, gdyż
na Antarktydzie nie ma niedźwiedzi. A niedźwiedź, oczywiście,
jest biały.


 ?
?