Zadanie ZM-1424
o zadaniu...
- Publikacja w Delcie: czerwiec 2014
- Publikacja elektroniczna: 02-06-2014
Udowodnić, że jedynym rozwiązaniem równania
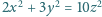 w zbiorze
liczb całkowitych jest
w zbiorze
liczb całkowitych jest
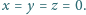
Udowodnić, że jedynym rozwiązaniem równania
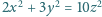 w zbiorze
liczb całkowitych jest
w zbiorze
liczb całkowitych jest
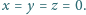
Zadanie 684 zaproponował pan Tomasz Ordowski.
Wykazać, że dla żadnej pary różnych liczb pierwszych 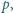
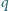 układ równań
układ równań
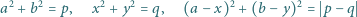
nie ma rozwiązań w liczbach całkowitych 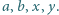
Znaleźć wszystkie funkcje
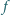 odwzorowujące zbiór liczb rzeczywistych
w siebie i spełniające dla każdych liczb rzeczywistych
odwzorowujące zbiór liczb rzeczywistych
w siebie i spełniające dla każdych liczb rzeczywistych
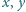 równanie
równanie
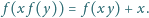 |
Rozważamy trójki liczb rzeczywistych
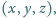 spełniające
warunki
spełniające
warunki
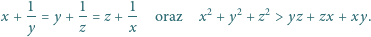 |
Wyznaczyć wszystkie możliwe wartości iloczynu
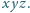
Zadanie 674 zaproponował pan Paweł Najman z Krakowa.
Znaleźć wszystkie funkcje
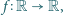 które spełniają układ równań
funkcyjnych
które spełniają układ równań
funkcyjnych
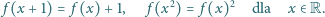
Udowodnić, że równanie
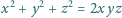
nie ma rozwiązania w liczbach całkowitych dodatnich.
Zadanie 664 zaproponował pan Tomasz Ordowski
Dowieść, że jeśli liczba rzeczywista
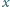 spełnia równanie
spełnia równanie
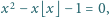 to każda potęga liczby
to każda potęga liczby
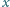 o wykładniku
dodatnim nieparzystym także spełnia to równanie.
o wykładniku
dodatnim nieparzystym także spełnia to równanie.
Rozstrzygnij, ile rozwiązań ma układ równań

Rozstrzygnij, ile rozwiązań ma układ równań

Liczby rzeczywiste
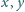 spełniają równość
spełniają równość
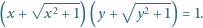
Udowodnić, że
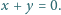
Znaleźć wszystkie funkcje określone na zbiorze liczb rzeczywistych dodatnich, o wartościach w tym samym zbiorze, spełniające nierówność
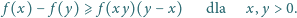
Rozwiązać równanie
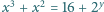 w liczbach całkowitych
w liczbach całkowitych
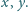
Udowodnij, że nie istnieją liczby nieparzyste
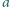 i
i
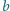 spełniające
równanie
spełniające
równanie
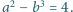
Znaleźć wszystkie funkcje
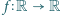 , spełniające równanie
, spełniające równanie