Zadanie ZM-1504
o zadaniu...
- Publikacja w Delcie: wrzesień 2016
- Publikacja elektroniczna: 1 września 2016
Rozstrzygnąć, czy istnieje liczba rzeczywista 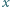 spełniająca równanie
spełniająca równanie
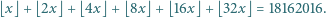
Rozstrzygnąć, czy istnieje liczba rzeczywista 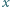 spełniająca równanie
spełniająca równanie
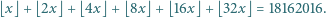
Czy istnieją takie funkcje kwadratowe 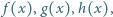 że równanie
że równanie 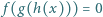 jest spełnione przez liczby 0, 1, 2, 3, 4, 5, 6, 7?
jest spełnione przez liczby 0, 1, 2, 3, 4, 5, 6, 7?
Zadanie 724 zostało opracowane na podstawie propozycji, którą przysłał pan Paweł Najman z Krakowa.
Dowieść, że liczby zespolone 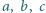 spełniają równanie
spełniają równanie
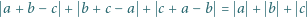
wtedy i tylko wtedy, gdy spełniają równanie
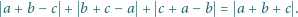
Zadanie 722 zaproponował pan Witold Bednarek z Łodzi.
Rozwiązać równanie 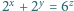 w liczbach całkowitych dodatnich
w liczbach całkowitych dodatnich 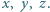
Wyznaczyć największą liczbę naturalną 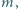 dla której istnieją takie liczby naturalne
dla której istnieją takie liczby naturalne 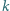 i
i 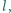 że spełnione jest równanie
że spełnione jest równanie
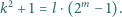
Rozstrzygnąć, czy istnieją liczby naturalne 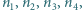 wszystkie większe od
wszystkie większe od 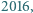 spełniające równanie
spełniające równanie

Znaleźć wszystkie wartości parametru 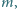 dla których wszystkie rozwiązania równania
dla których wszystkie rozwiązania równania
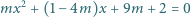
są liczbami naturalnymi.
Znajdź wszystkie trójki dodatnich liczb całkowitych  dla których
dla których 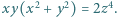
Znajdź wszystkie pary liczb całkowitych 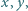 dla których
dla których 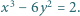
Zadanie 712 zaproponował pan Paweł Kubit z Krakowa.
Liczby rzeczywiste 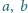 spełniają równania:
spełniają równania:
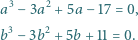
Obliczyć wartość sumy 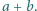
Niech 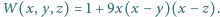 Znaleźć wszystkie trójki liczb zespolonych
Znaleźć wszystkie trójki liczb zespolonych 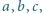 dla których spełnione jest równanie
dla których spełnione jest równanie 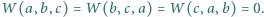
Wykaż, że istnieje nieskończenie wiele trójek 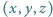 dodatnich liczb całkowitych spełniających równanie
dodatnich liczb całkowitych spełniających równanie

Udowodnić, że dla liczby całkowitej dodatniej 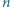 oraz liczb rzeczywistych
oraz liczb rzeczywistych  spełniających
spełniających 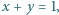 prawdziwa jest tożsamość
prawdziwa jest tożsamość
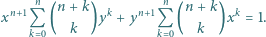
Zadanie 702 zaproponował pan Piotr Kumor z Olsztyna.
Niech 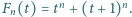 Udowodnić, że istnieje nieskończenie wiele liczb całkowitych
Udowodnić, że istnieje nieskończenie wiele liczb całkowitych 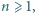 dla których równanie
dla których równanie 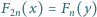 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 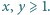
Na płaszczyźnie dany jest skończony zbiór punktów, wśród których żadne trzy nie leżą na jednej prostej. Niech 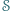 oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta
oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta 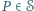 przez
przez 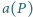 i
i 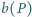 oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta
oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta 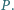 Wykazać, że dla każdej liczby rzeczywistej
Wykazać, że dla każdej liczby rzeczywistej  zachodzi równość
zachodzi równość
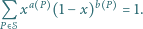
Znaleźć wszystkie pary wielomianów rzeczywistych 
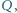 spełniające równanie
spełniające równanie
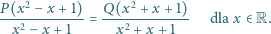
Wyznaczyć wszystkie liczby rzeczywiste 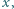 które spełniają równanie
które spełniają równanie 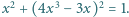
Liczby całkowite dodatnie 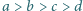 spełniają równanie
spełniają równanie

Udowodnić, że liczba 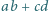 nie jest liczbą pierwszą.
nie jest liczbą pierwszą.
Rozwiąż równanie 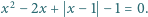
Zadanie 686 zaproponował pan Paweł Kubit z Krakowa
Udowodnić, że istnieje nieskończenie wiele liczb naturalnych 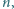 dla których równanie
dla których równanie 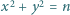 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 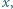
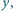 różnych od zera, ale ma rozwiązania w liczbach wymiernych
różnych od zera, ale ma rozwiązania w liczbach wymiernych 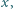
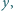 różnych od zera.
różnych od zera.