Kąty dwuścienne»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: Olimpiada Matematyczna 45-I-12
- Zadanie pochodzi z artykułu Kąty dwuścienne
- Publikacja w Delcie: październik 2011
- Publikacja elektroniczna: 02-10-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (64 KB)
Wykazać, że sumy przeciwległych kątów dwuściennych czworościanu są równe wtedy i tylko wtedy, gdy sumy długości przeciwległych krawędzi są równe.
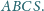 Krawędzie podstawy mają
długości
Krawędzie podstawy mają
długości
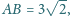
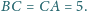 Krawędzie boczne mają
długości
Krawędzie boczne mają
długości
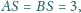
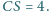 Oblicz objętość tego
ostrosłupa.
Oblicz objętość tego
ostrosłupa.
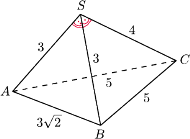
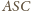 jest trójkątem o bokach długości
jest trójkątem o bokach długości
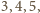 ma zatem
kąt prosty przy wierzchołku
ma zatem
kąt prosty przy wierzchołku
 Analogicznie
Analogicznie
 Ściana
Ściana
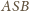 ma boki długości
ma boki długości
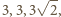 czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
 Ustawmy dany
ostrosłup inaczej: niech
Ustawmy dany
ostrosłup inaczej: niech
 będzie podstawą. Wobec powyższych
obserwacji
będzie podstawą. Wobec powyższych
obserwacji
 jest wtedy wysokością i
jest wtedy wysokością i
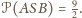 Stąd
objętość ostrosłupa to
Stąd
objętość ostrosłupa to
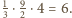
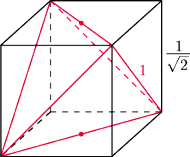
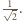 Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
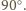 Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
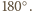 W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
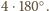 Sprzeczność, gdyż ta suma jest równa
Sprzeczność, gdyż ta suma jest równa
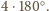
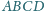 kąty
kąty
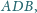
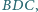
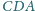 są
rozwarte, a krawędzie
są
rozwarte, a krawędzie
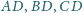 są równe. Dowieść, że trójkąt
są równe. Dowieść, że trójkąt
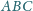 jest ostrokątny.
jest ostrokątny.
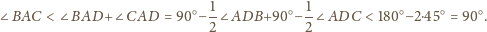
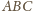 są ostre.
są ostre.
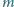 będzie liczbą krawędzi czworościanu o długości
będzie liczbą krawędzi czworościanu o długości
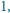 a
a
 liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
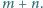
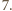
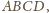 w którym
w którym
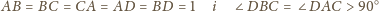
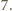 Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
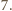 Wynika stąd w szczególności, że liczba krawędzi
długości
Wynika stąd w szczególności, że liczba krawędzi
długości
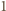 jest równa co najmniej
jest równa co najmniej
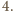 Jeśli jest
Jeśli jest
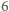 krawędzi
długości
krawędzi
długości
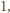 to nie ma kątów rozwartych. Jeśli jest
to nie ma kątów rozwartych. Jeśli jest
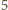 krawędzi
długości
krawędzi
długości
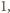 to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
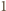 musi być równa
musi być równa
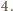 Tym samym
liczba kątów rozwartych musi być równa
Tym samym
liczba kątów rozwartych musi być równa
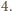 Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
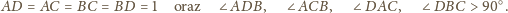
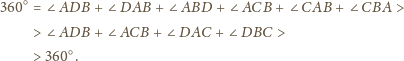
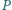 będzie dowolnym punktem wewnątrz czworościanu
będzie dowolnym punktem wewnątrz czworościanu
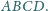 Dowieść, że
Dowieść, że

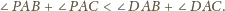
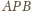 przecina krawędź
przecina krawędź
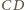 w
punkcie
w
punkcie
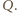 Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
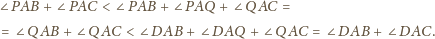
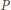 leży wewnątrz trójkąta
leży wewnątrz trójkąta
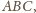 to
to
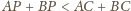 –
wystarczy rozważyć sferę o środku
–
wystarczy rozważyć sferę o środku
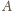 i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
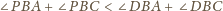
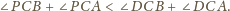
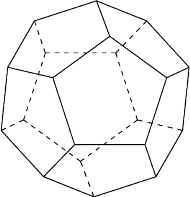
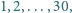 używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
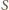 oznacza sumę wszystkich numerów
krawędzi:
oznacza sumę wszystkich numerów
krawędzi:
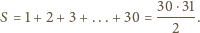
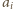 oznacza sumę numerów w
oznacza sumę numerów w
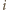 -tym wierzchołku (
-tym wierzchołku (
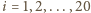 ). Wtedy
). Wtedy
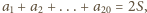 bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
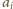 była podzielna przez 4, to
była podzielna przez 4, to
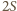 także. Jednak
także. Jednak
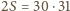 nie dzieli się przez 4.
nie dzieli się przez 4.
 oznacza ich sumę, a
oznacza ich sumę, a
 – sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
– sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
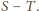 Początkowo
Początkowo
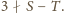 Tymczasem gdyby
Tymczasem gdyby
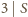 i
i
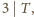 to
to
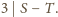
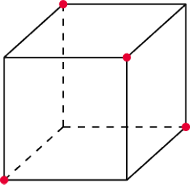
 można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.
można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.
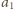 i
i
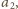
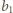 i
i
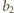 oraz
oraz
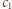 i
i
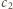 liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
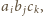 gdzie
gdzie
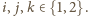 Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako
Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako
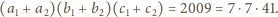
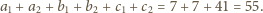
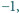 a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
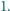 Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
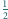 w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
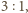 licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
 można wpisać kulę
można wpisać kulę
 o środku
o środku
 i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
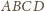 przez jednokładność względem punktu
przez jednokładność względem punktu
 o skali
o skali
 W efekcie otrzymamy czworościan
W efekcie otrzymamy czworościan
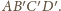 Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
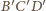 przecina wysokość
przecina wysokość
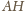 w punkcie
w punkcie
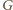 w taki
sposób, że
w taki
sposób, że
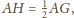 a kula
a kula
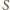 jest również styczna do
płaszczyzny
jest również styczna do
płaszczyzny
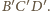 Zatem kula
Zatem kula
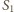 wpisana w czworościan
wpisana w czworościan
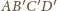 ma promień
ma promień
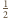 i ma tylko jeden punkt wspólny z kulą
i ma tylko jeden punkt wspólny z kulą
 umieszczone w każdym „rogu” czworościanu
umieszczone w każdym „rogu” czworościanu
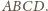 Każda z tych kul
ma tylko jeden punkt wspólny z kulą
Każda z tych kul
ma tylko jeden punkt wspólny z kulą
 Ponieważ kula
Ponieważ kula
 ma
promień 1, więc można umieścić w niej dwie kule o promieniu
ma
promień 1, więc można umieścić w niej dwie kule o promieniu
 które mają tylko jeden punkt wspólny.
które mają tylko jeden punkt wspólny.
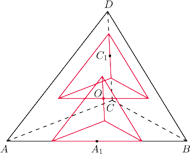
 będą odpowiednio środkami krawędzi
będą odpowiednio środkami krawędzi
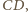
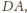
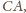
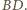 Przekształćmy kulę
Przekształćmy kulę
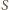 i czworościan
i czworościan
 przez
przez  i skali
i skali
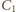 i skali
i skali
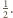
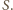 Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
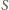 przez
przez 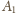 i skali
i skali
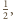
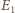 i skali
i skali
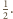
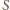 będą środki kul o promieniach
będą środki kul o promieniach
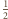 znajdujące się w połowie odcinków
znajdujące się w połowie odcinków
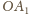 i
i
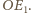 Wykażemy teraz,
że kule te nie mają punktów wspólnych.
Wykażemy teraz,
że kule te nie mają punktów wspólnych.
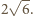 Zatem odległość
punktów
Zatem odległość
punktów
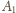 i
i
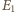 wynosi
wynosi
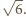 Środki boków
Środki boków
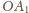 i
i
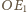 w trójkącie
w trójkącie
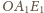 pozostają w odległości
pozostają w odległości
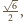 która
jest większa od 1.
która
jest większa od 1.
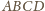 można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
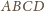 w
jednokładności o skali
w
jednokładności o skali
 i środku będącym środkiem krawędzi
czworościanu.
i środku będącym środkiem krawędzi
czworościanu.
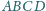 jest styczna do ścian
jest styczna do ścian
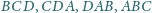 odpowiednio w punktach
odpowiednio w punktach
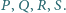 Odcinek
Odcinek
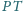 jest średnicą tej sfery, zaś punkty
jest średnicą tej sfery, zaś punkty
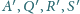 są
punktami przecięcia prostych
są
punktami przecięcia prostych
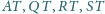 z płaszczyzną
z płaszczyzną
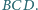 Dowieść , że punkt
Dowieść , że punkt
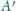 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
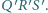
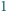 od jego wierzchołków jest
nie większa niż
od jego wierzchołków jest
nie większa niż
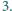
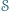 jest styczna do krawędzi
jest styczna do krawędzi
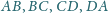 czworościanu
czworościanu
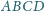 dpowiednio w punktach
dpowiednio w punktach
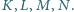 Wykaż, że leżą one
na jednej płaszczyźnie.
Wykaż, że leżą one
na jednej płaszczyźnie.
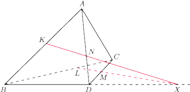
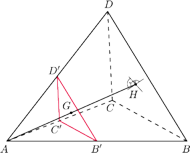
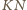 przecina prostą
przecina prostą
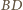 w pewnym punkcie
w pewnym punkcie
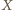 (poza odcinkiem
(poza odcinkiem
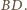 Wtedy z twierdzenia Menelaosa dla
trójkąta
Wtedy z twierdzenia Menelaosa dla
trójkąta
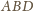 i prostej
i prostej
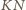 mamy
mamy
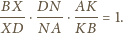
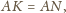
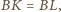
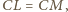
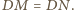 Wobec powyższego
Wobec powyższego
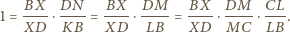
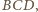 prosta
prosta
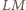 przecina prostą
przecina prostą
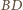 w punkcie
w punkcie
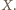 Stąd proste
Stąd proste
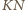 i
i
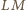 przecinają się, więc punkty
przecinają się, więc punkty
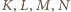 leżą na jednej
płaszczyźnie. Prostszy przypadek
leżą na jednej
płaszczyźnie. Prostszy przypadek
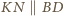 pozostawiam jako
ćwiczenie.
pozostawiam jako
ćwiczenie.
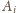 oraz
długość krawędzi wychodzących z wierzchołka
oraz
długość krawędzi wychodzących z wierzchołka
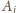 przez
przez
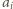 ,
gdzie
,
gdzie
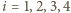 . Wtedy krawędź
. Wtedy krawędź
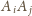 , gdzie
, gdzie
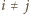 ,
wychodzi z wierzchołka
,
wychodzi z wierzchołka
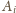 oraz z wierzchołka
oraz z wierzchołka
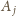 . Oznacza to,
że
. Oznacza to,
że
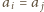 , a więc czworościan jest foremny.
, a więc czworościan jest foremny.