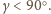Klub 44M - zadania X 2014»Zadanie 688
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania X 2014
- Publikacja w Delcie: październik 2014
- Publikacja elektroniczna: 1 października 2014
- Artykuł źródłowy w wersji do druku [application/pdf]: (66 KB)
-
Zadanie 688 zaproponował pan Witold Bednarek z Łodzi.
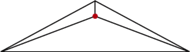
Trójkąt równoboczny 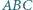 o boku długości 1 jest podstawą ostrosłupa prawidłowego
o boku długości 1 jest podstawą ostrosłupa prawidłowego 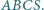 Na krawędziach
Na krawędziach 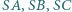 leżą takie punkty
leżą takie punkty 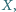
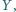
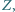 że suma kwadratów pól trójkątów
że suma kwadratów pól trójkątów  jest równa kwadratowi pola trójkąta
jest równa kwadratowi pola trójkąta 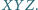 Obliczyć objętość ostrosłupa
Obliczyć objętość ostrosłupa 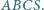
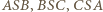 są przystającymi trójkątami równoramiennymi, z jednakowym kątem
są przystającymi trójkątami równoramiennymi, z jednakowym kątem 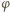 przy wierzchołku
przy wierzchołku 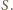 Niech
Niech 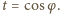 Oznaczając
Oznaczając 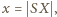
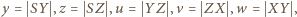 mamy
mamy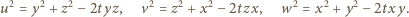
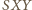 wynosi
wynosi 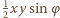 ; podobnie wyrażają się pola trójkątów
; podobnie wyrażają się pola trójkątów 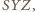
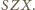 Suma kwadratów ich pól jest równa
Suma kwadratów ich pól jest równa 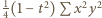 ; tu i dalej symbol
; tu i dalej symbol 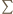 oznacza sumę cykliczną względem trójki
oznacza sumę cykliczną względem trójki 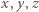 (lub
(lub  ).
).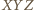 wyrażamy zgodnie ze wzorem Herona jako
wyrażamy zgodnie ze wzorem Herona jako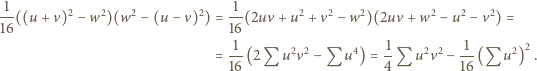
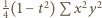 ; mnożąc przez 4 dostajemy równanie
; mnożąc przez 4 dostajemy równanie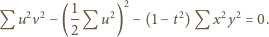
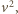
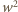 wyrażeń (1) i pogrupowaniu wszystkiego według potęg
wyrażeń (1) i pogrupowaniu wszystkiego według potęg 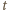 (to mechaniczny rachunek) okazuje się, że wyrazy niezawierające
(to mechaniczny rachunek) okazuje się, że wyrazy niezawierające 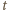 znoszą się, a całe równanie (2) redukuje się do postaci
znoszą się, a całe równanie (2) redukuje się do postaci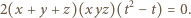
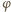 jest niezerowy, więc
jest niezerowy, więc 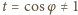 ; stąd
; stąd 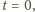 czyli
czyli 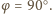 Zatem każdy z trójkątów
Zatem każdy z trójkątów 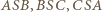 jest prostokątny i równoramienny, o przeciwprostokątnej długości 1; przyprostokątne
jest prostokątny i równoramienny, o przeciwprostokątnej długości 1; przyprostokątne 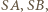
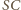 mają długość
mają długość 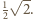 Ostrosłup
Ostrosłup 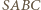 jest szóstą częścią sześcianu o krawędzi
jest szóstą częścią sześcianu o krawędzi 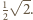 Jego objętość wynosi
Jego objętość wynosi 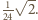
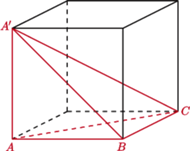
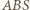 i
i  ostrosłupa z rysunku są prostopadłe do podstawy.
ostrosłupa z rysunku są prostopadłe do podstawy.
 (na ścianę
(na ścianę  ) nie ma wspólnych punktów z wysokością
) nie ma wspólnych punktów z wysokością 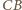 (na ścianę
(na ścianę 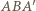 ), tym bardziej nie można więc oczekiwać wspólnego punktu dla wszystkich czterech wysokości.
), tym bardziej nie można więc oczekiwać wspólnego punktu dla wszystkich czterech wysokości.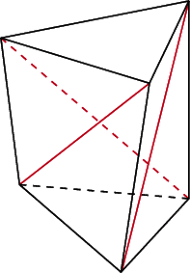
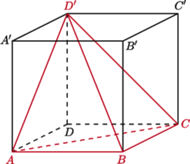
 to punkt
to punkt  Wysokość z wierzchołka
Wysokość z wierzchołka 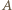 zawarta jest w prostej
zawarta jest w prostej 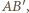 prostopadłej do płaszczyzny
prostopadłej do płaszczyzny 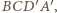 więc spodek tej wysokości to środek przedniej ściany sześcianu. Analogicznie spodkiem wysokości z wierzchołka
więc spodek tej wysokości to środek przedniej ściany sześcianu. Analogicznie spodkiem wysokości z wierzchołka 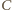 jest środek kwadratu
jest środek kwadratu 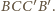 Przekątna
Przekątna 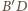 sześcianu jest prostopadła do ściany
sześcianu jest prostopadła do ściany 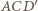 czworościanu, zatem wysokość z wierzchołka
czworościanu, zatem wysokość z wierzchołka 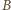 jest równoległa do
jest równoległa do 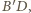 a co za tym idzie jej spodek również trafia poza odpowiednią podstawę.
a co za tym idzie jej spodek również trafia poza odpowiednią podstawę.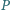 będzie pewnym wielościanem. Udowodnić, że istnieje stała
dodatnia
będzie pewnym wielościanem. Udowodnić, że istnieje stała
dodatnia
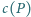 o następującej własności: jeśli pewnych
o następującej własności: jeśli pewnych
 kul
o sumie objętości
kul
o sumie objętości
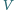 pokrywa wszystkie ściany (czyli każdy
punkt każdej ściany
pokrywa wszystkie ściany (czyli każdy
punkt każdej ściany
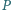 należy do co najmniej jednej z nich),
to
należy do co najmniej jednej z nich),
to
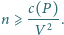
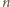 kul o promieniach
kul o promieniach
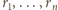 spełnia
podaną własność (pokrywa wszystkie ściany
spełnia
podaną własność (pokrywa wszystkie ściany
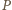 ). Wówczas
). Wówczas
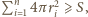 gdzie
gdzie
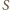 to pole powierzchni bocznej
to pole powierzchni bocznej
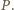 Ponadto
Ponadto
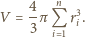
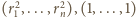 i wag
i wag
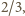
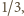 otrzymujemy
otrzymujemy
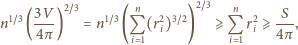
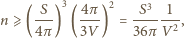
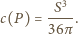
 w przestrzeni, definiujemy zbiór
w przestrzeni, definiujemy zbiór
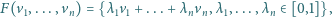
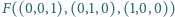 to standardowa kostka. Rozstrzygnąć,
czy dla pewnych wektorów można w ten sposób otrzymać ośmiościan
foremny.
to standardowa kostka. Rozstrzygnąć,
czy dla pewnych wektorów można w ten sposób otrzymać ośmiościan
foremny.
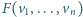 w geometrii wypukłej nazywa się sumą
Minkowskiego odcinków
w geometrii wypukłej nazywa się sumą
Minkowskiego odcinków
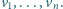
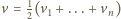 jest środkiem
symetrii zbioru
jest środkiem
symetrii zbioru
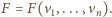 Istotnie, symetria
Istotnie, symetria
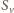 o środku
o środku
 przeprowadza wektor
przeprowadza wektor
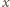 na
na
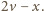 Dla dowolnego
Dla dowolnego
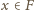 w postaci
w postaci
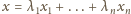 mamy
mamy
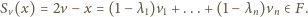
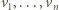 zbiór
zbiór
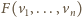 to ośmiościan foremny
to ośmiościan foremny
 i że
i że
 jest
najmniejsze możliwe (oczywiście
jest
najmniejsze możliwe (oczywiście
 ). Zauważmy, że wtedy
). Zauważmy, że wtedy
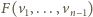 jest ścianą
jest ścianą
 czyli trójkątem równobocznym,
który nie ma środka symetrii – sprzeczność.
czyli trójkątem równobocznym,
który nie ma środka symetrii – sprzeczność.
 w jego
wnętrzu. Suma odległości punktu
w jego
wnętrzu. Suma odległości punktu
 od krawędzi tego czworościanu jest
równa
od krawędzi tego czworościanu jest
równa
 Wykaż, że
Wykaż, że
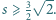
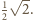
 od dwóch przeciwległych krawędzi
czworościanu jest nie mniejsza od sumy odległości
od dwóch przeciwległych krawędzi
czworościanu jest nie mniejsza od sumy odległości
 od zawierających
je przeciwległych ścian sześcianu, która z kolei jest większa lub równa
odległości pomiędzy takimi ścianami, czyli długości krawędzi sześcianu.
Czworościan ma trzy pary przeciwległych krawędzi, stąd
od zawierających
je przeciwległych ścian sześcianu, która z kolei jest większa lub równa
odległości pomiędzy takimi ścianami, czyli długości krawędzi sześcianu.
Czworościan ma trzy pary przeciwległych krawędzi, stąd
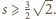
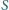 i
i
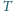 o następujących dwóch
własnościach:
o następujących dwóch
własnościach:
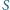 jest większa od objętości
czworościanu
jest większa od objętości
czworościanu
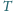 ;
;
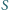 nie przekracza pola
żadnej ściany czworościanu
nie przekracza pola
żadnej ściany czworościanu
 zbudujemy czworościan
zbudujemy czworościan
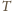 o żądanych własnościach. Niech
o żądanych własnościach. Niech
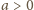 będzie taką liczbą, aby
liczba
będzie taką liczbą, aby
liczba
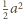 była większa od pola każdej ściany czworościanu
była większa od pola każdej ściany czworościanu
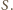 Niech
Niech
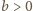 będzie taką liczbą, aby liczba
będzie taką liczbą, aby liczba
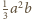 była
mniejsza od objętości czworościanu
była
mniejsza od objętości czworościanu
 będzie czworościanem wpisanym w prostopadłościan
o podstawie
będzie czworościanem wpisanym w prostopadłościan
o podstawie
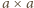 i wysokości
i wysokości
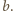 Objętość
Objętość
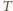 równa
jest
równa
jest
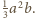 Każdą ścianę czworościanu
Każdą ścianę czworościanu
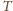 można
zrzutować na połowę podstawy prostopadłościanu, więc jej pole
przekracza
można
zrzutować na połowę podstawy prostopadłościanu, więc jej pole
przekracza
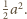 Z definicji liczb
Z definicji liczb
 i
i
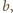 czworościany
czworościany
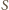 i
i
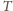 spełniają żądane warunki.
spełniają żądane warunki.
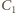 i
i
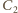 wpisane
odpowiednio w prostopadłościany o wymiarach
wpisane
odpowiednio w prostopadłościany o wymiarach
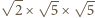 oraz
oraz
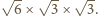
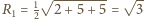 oraz
oraz
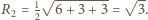
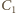 jest
trójkątem o bokach
jest
trójkątem o bokach
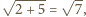
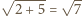 oraz
oraz
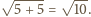 Wysokość takiego trójkąta, opuszczona na bok
o długości
Wysokość takiego trójkąta, opuszczona na bok
o długości
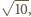 równa jest
równa jest
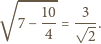
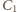 równe jest
równe jest
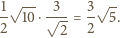
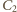 też równe jest
też równe jest
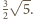
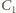 i
i
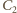 mają więc równe pola ścian
i promienie kul opisanych. Tymczasem ich objętości są różne:
mają więc równe pola ścian
i promienie kul opisanych. Tymczasem ich objętości są różne:
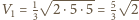 oraz
oraz
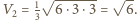

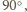 czyli trzeciemu kątowi.
czyli trzeciemu kątowi.

 w którym
w którym

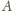 spełniają warunek
spełniają warunek
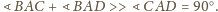 Z kolei rozważając kąt trójścienny
przy
Z kolei rozważając kąt trójścienny
przy
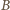 oraz trójkąty prostokątne
oraz trójkąty prostokątne
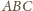 i
i
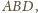 wnioskujemy,
że
wnioskujemy,
że
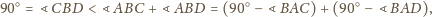
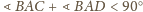 – sprzeczność.
– sprzeczność.
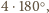 jako
suma kątów czterech trójkątów. Wobec tego istnieje taki wierzchołek
czworościanu, przy którym suma trzech kątów płaskich nie przekracza
jako
suma kątów czterech trójkątów. Wobec tego istnieje taki wierzchołek
czworościanu, przy którym suma trzech kątów płaskich nie przekracza
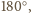 w przeciwnym razie suma wszystkich kątów płaskich czworościanu
przekraczałaby
w przeciwnym razie suma wszystkich kątów płaskich czworościanu
przekraczałaby
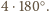
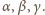 Wówczas
Wówczas
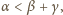 więc
więc
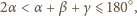
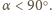 Analogicznie
Analogicznie
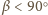 oraz
oraz