Wielościany w wielościanach, czyli matematyka eksperymentalna»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Wielościany w wielościanach, czyli matematyka eksperymentalna
- Publikacja w Delcie: sierpień 2020
- Publikacja elektroniczna: 1 sierpnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (560 KB)
"Sześcian w Dwudziestościanie".
W dwudziestościanie foremnym zawarty jest sześcian o największej możliwej objętości. Jaką część objętości dwudziestościanu zajmuje ten sześcian?
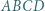 wszystkie kąty płaskie przy wierzchołku
wszystkie kąty płaskie przy wierzchołku 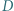 mają miarę
mają miarę 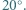 Wykazać, że
Wykazać, że 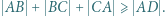
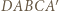 będzie siatką tego czworościanu po rozcięciu wzdłuż krawędzi
będzie siatką tego czworościanu po rozcięciu wzdłuż krawędzi 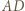 i usunięciu ściany
i usunięciu ściany 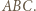 Wówczas trójkąt
Wówczas trójkąt 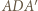 jest równoboczny.
jest równoboczny.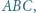 w którym
w którym 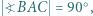 jest podstawą ostrosłupa
jest podstawą ostrosłupa 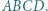 Ponadto zachodzą równości
Ponadto zachodzą równości 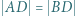 oraz
oraz 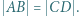 Udowodnić, że
Udowodnić, że 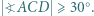
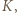 by czworokąt
by czworokąt 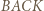 był prostokątem. Wtedy trójkąt
był prostokątem. Wtedy trójkąt 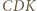 jest równoboczny. Z nierówności kąta trójściennego mamy
jest równoboczny. Z nierówności kąta trójściennego mamy 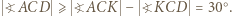
 jest częścią wspólną sfer
jest częścią wspólną sfer  i
i 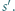 Trzy różne punkty
Trzy różne punkty 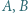 i
i 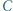 leżą na okręgu
leżą na okręgu  Punkt
Punkt 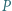 leży na sferze
leży na sferze 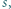 na zewnątrz sfery
na zewnątrz sfery 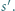 Prosta
Prosta 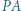 przecina sferę
przecina sferę 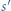 w punkcie
w punkcie 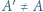 ; analogicznie określamy punkty
; analogicznie określamy punkty 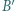 i
i 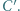 Dowieść, że płaszczyzna
Dowieść, że płaszczyzna 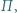 przechodząca przez punkt
przechodząca przez punkt 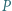 i styczna do sfery
i styczna do sfery 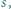 jest równoległa do płaszczyzny
jest równoległa do płaszczyzny 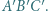
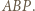 Oznaczmy przez
Oznaczmy przez 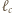 prostą będącą częścią wspólną płaszczyzn
prostą będącą częścią wspólną płaszczyzn 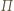 i
i 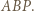 Rachunek na kątach dowodzi, że
Rachunek na kątach dowodzi, że 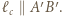 Analogicznie, dla przekroju płaszczyzną
Analogicznie, dla przekroju płaszczyzną 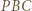 można dowieść, że
można dowieść, że 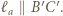
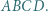 Punkt
Punkt 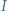 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 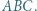 Punkt
Punkt 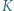 leży na odcinku
leży na odcinku 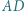 i spełnia warunek
i spełnia warunek
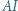 i
i 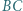 przecinają się w punkcie
przecinają się w punkcie 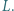 Dowieść, że prosta
Dowieść, że prosta 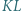 przechodzi przez środek odcinka
przechodzi przez środek odcinka 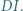
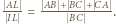 Teraz wystarczy zastosować twierdzenie Menelaosa dla trójkąta
Teraz wystarczy zastosować twierdzenie Menelaosa dla trójkąta 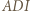 i prostej
i prostej 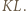
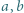 i
i  Wyznaczyć najkrótszą drogę łączącą dwa przeciwległe wierzchołki tego prostopadłościanu, biegnącą po jego powierzchni.
Wyznaczyć najkrótszą drogę łączącą dwa przeciwległe wierzchołki tego prostopadłościanu, biegnącą po jego powierzchni.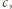 otrzymując z sąsiadujących ścian prostokąt o bokach
otrzymując z sąsiadujących ścian prostokąt o bokach  i
i 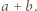 Poszukiwana najkrótsza droga wiedzie po linii prostej, czyli wzdłuż przekątnej tego prostokąta. Jej długość to
Poszukiwana najkrótsza droga wiedzie po linii prostej, czyli wzdłuż przekątnej tego prostokąta. Jej długość to 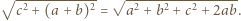 Dwa analogiczne wyniki otrzymamy dla krawędzi
Dwa analogiczne wyniki otrzymamy dla krawędzi 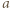 i
i 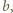 więc powyższa droga jest najkrótsza, jeśli
więc powyższa droga jest najkrótsza, jeśli 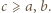
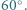 Dowieść, że obwód podstawy tego ostrosłupa jest nie mniejszy od długości każdej jego bocznej krawędzi.
Dowieść, że obwód podstawy tego ostrosłupa jest nie mniejszy od długości każdej jego bocznej krawędzi.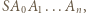 w którym
w którym 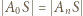 i
i 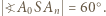 Z tego wynika, że trójkąt
Z tego wynika, że trójkąt 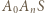 jest równoboczny. Brzeg podstawy ostrosłupa na narysowanej siatce jest łamaną
jest równoboczny. Brzeg podstawy ostrosłupa na narysowanej siatce jest łamaną 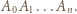
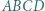 zachodzą równości
zachodzą równości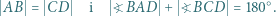
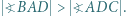
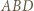 i
i 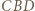 jest trapezem równoramiennym.
jest trapezem równoramiennym.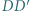 jest wysokością czworościanu
jest wysokością czworościanu 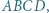 w którym zachodzą równości
w którym zachodzą równości
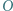 będzie środkiem okręgu opisanego na trójkącie
będzie środkiem okręgu opisanego na trójkącie 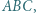 zaś
zaś 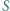 środkiem ciężkości tego trójkąta. Dowieść, że punkty
środkiem ciężkości tego trójkąta. Dowieść, że punkty 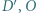 i
i 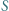 leżą na jednej prostej.
leżą na jednej prostej.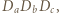 w którym punkty
w którym punkty 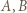 i
i 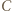 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 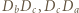 i
i 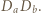 Punkt
Punkt 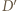 jest ortocentrum trójkąta
jest ortocentrum trójkąta 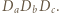 Wystarczy skorzystać z twierdzenia o prostej Eulera.
Wystarczy skorzystać z twierdzenia o prostej Eulera.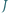 sfery wpisanej oraz środek
sfery wpisanej oraz środek 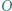 sfery opisanej na czworościanie
sfery opisanej na czworościanie 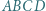 przecina krawędź
przecina krawędź 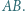 Wykazać, że miary kątów
Wykazać, że miary kątów 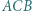 i
i 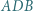 są równe lub sumują się do
są równe lub sumują się do 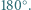
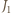 oraz
oraz 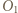 punktów
punktów 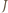 oraz
oraz 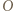 na płaszczyznę
na płaszczyznę 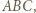 analogicznie
analogicznie 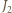 oraz
oraz 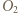 na płaszczyznę
na płaszczyznę 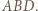 Ponieważ
Ponieważ 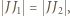 otrzymujemy
otrzymujemy 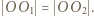 Dalej, z twierdzenia Pitagorasa, okręgi opisane na ścianach
Dalej, z twierdzenia Pitagorasa, okręgi opisane na ścianach 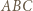 i
i 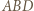 mają równe promienie. Teza wynika z twierdzenia sinusów.
mają równe promienie. Teza wynika z twierdzenia sinusów.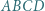 wszystkie wewnętrzne kąty dwuścienne są ostre. Punkt
wszystkie wewnętrzne kąty dwuścienne są ostre. Punkt 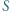 leży wewnątrz tego czworościanu, a jego odległość od każdej z płaszczyzn
leży wewnątrz tego czworościanu, a jego odległość od każdej z płaszczyzn 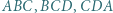 i
i 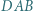 jest większa niż
jest większa niż 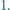 Dowieść, że przynajmniej dwa spośród odcinków
Dowieść, że przynajmniej dwa spośród odcinków 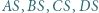 mają długość większą niż
mają długość większą niż 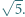
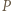 na płaszczyznę
na płaszczyznę 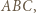 otrzymamy punkt
otrzymamy punkt 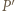 leżący wewnątrz trójkąta
leżący wewnątrz trójkąta 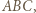 którego odległość od każdego z boków tego trójkąta jest większa od
którego odległość od każdego z boków tego trójkąta jest większa od 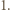 Któryś z kątów trójkąta
Któryś z kątów trójkąta 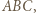 powiedzmy kąt
powiedzmy kąt 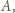 ma miarę nieprzekraczającą
ma miarę nieprzekraczającą 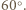 Stąd
Stąd 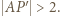 Mamy też
Mamy też 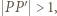 więc z twierdzenia Pitagorasa dla trójkąta
więc z twierdzenia Pitagorasa dla trójkąta 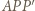 otrzymamy
otrzymamy 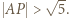 Powtarzając to rozumowanie dla płaszczyzny
Powtarzając to rozumowanie dla płaszczyzny 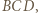 otrzymamy tezę.
otrzymamy tezę.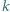 przecinamy płaszczyzną
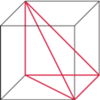
przecinamy płaszczyzną 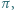 położoną w odległości
położoną w odległości 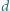 od środka sześcianu. Jaka jest maksymalna wartość
od środka sześcianu. Jaka jest maksymalna wartość 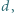 przy której płaszczyzna
przy której płaszczyzna 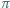 może mieć z każdą ścianą sześcianu co najmniej jeden punkt wspólny?
może mieć z każdą ścianą sześcianu co najmniej jeden punkt wspólny?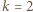 i ustalmy prostokątny układ współrzędnych, w którym wierzchołkami sześcianu są punkty
i ustalmy prostokątny układ współrzędnych, w którym wierzchołkami sześcianu są punkty 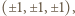 a rzutem prostokątnym punktu
a rzutem prostokątnym punktu 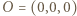 na płaszczyznę
na płaszczyznę 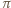 jest punkt
jest punkt 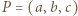 o współrzędnych
o współrzędnych 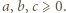 Zatem
Zatem 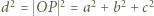 ; zaś płaszczyzna
; zaś płaszczyzna 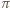 jest dana równaniem
jest dana równaniem 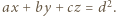
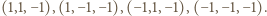 Każda z półprzestrzeni (
Każda z półprzestrzeni ( 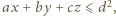
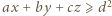 ) musi zawierać jeden z tych czterech wierzchołków. Zatem przy pewnym doborze znaków mamy nierówność
) musi zawierać jeden z tych czterech wierzchołków. Zatem przy pewnym doborze znaków mamy nierówność 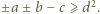 Skoro
Skoro 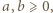 znaczy to, że
znaczy to, że 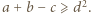
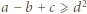 oraz
oraz 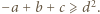 Dodajemy te trzy nierówności i otrzymujemy
Dodajemy te trzy nierówności i otrzymujemy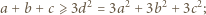
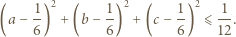
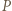 od punktu
od punktu 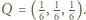 Tak więc
Tak więc 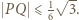 A ponieważ
A ponieważ 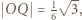 ostatecznie
ostatecznie 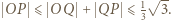
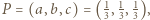 wszystkie nierówności stają się równościami; płaszczyzna o równaniu
wszystkie nierówności stają się równościami; płaszczyzna o równaniu 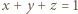 leży w odległości
leży w odległości 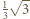 od
od 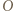 i spotyka wszystkie ściany. Dla
i spotyka wszystkie ściany. Dla 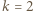 szukane maksimum wynosi więc
szukane maksimum wynosi więc 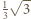 ; zaś w przypadku ogólnym - po przeskalowaniu - wynosi
; zaś w przypadku ogólnym - po przeskalowaniu - wynosi 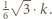
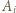 będzie wierzchołkiem kostki, odległym od stołu o
będzie wierzchołkiem kostki, odległym od stołu o 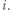 Oznaczmy długość krawędzi kostki przez
Oznaczmy długość krawędzi kostki przez  Łatwo zauważyć, że odcinki
Łatwo zauważyć, że odcinki 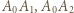 oraz
oraz 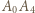 muszą być krawędziami sześcianu (wynika to z faktu, że jeśli krawędziami są
muszą być krawędziami sześcianu (wynika to z faktu, że jeśli krawędziami są 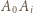 i
i 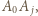 to
to 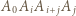 jest ścianą). Niech
jest ścianą). Niech 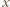 będzie długością krawędzi sześcianu. Dobierzmy układ współrzędnych tak, by
będzie długością krawędzi sześcianu. Dobierzmy układ współrzędnych tak, by 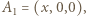
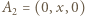 i
i 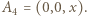 Oznaczmy przez
Oznaczmy przez 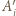 rzut prostokątny punktu
rzut prostokątny punktu 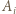 na prostą prostopadłą do stołu, przechodzącą przez
na prostą prostopadłą do stołu, przechodzącą przez 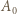 ; wówczas
; wówczas 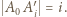 Przyjmijmy
Przyjmijmy 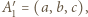 wtedy
wtedy 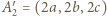 i
i 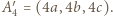 Korzystając z twierdzenia Pitagorasa dla trójkątów prostokątnych
Korzystając z twierdzenia Pitagorasa dla trójkątów prostokątnych 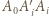 dla
dla 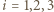 dostajemy
dostajemy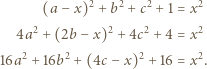
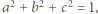 dostajemy
dostajemy 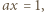
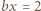 i
i 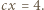 Po podniesieniu ostatnich trzech równości do kwadratu i zsumowaniu, otrzymamy
Po podniesieniu ostatnich trzech równości do kwadratu i zsumowaniu, otrzymamy 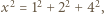 zatem
zatem 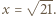

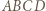 w którym
w którym 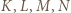 są punktami styczności sfery wpisanej i ścian leżących odpowiednio naprzeciw wierzchołków
są punktami styczności sfery wpisanej i ścian leżących odpowiednio naprzeciw wierzchołków 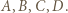
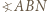 oraz
oraz 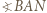 w zależności od miar kątów wewnętrznych ścian czworościanu (które są dane, gdy dana jest siatka).
w zależności od miar kątów wewnętrznych ścian czworościanu (które są dane, gdy dana jest siatka).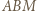 i
i 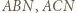 i
i 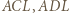 i
i 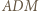 to pary trójkątów przystających; oznaczmy kąty wewnętrzne przy wierzchołku
to pary trójkątów przystających; oznaczmy kąty wewnętrzne przy wierzchołku 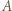 w poszczególnych z nich odpowiednio przez
w poszczególnych z nich odpowiednio przez 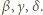 Wówczas
Wówczas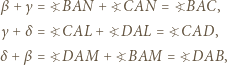
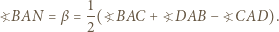
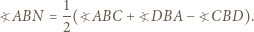
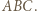 Dla pozostałych ścian konstrukcja jest w pełni analogiczna.
Dla pozostałych ścian konstrukcja jest w pełni analogiczna.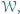 który można rozciąć płaszczyzną na dwa wielościany podobne do
który można rozciąć płaszczyzną na dwa wielościany podobne do 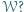
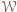 o wymiarach
o wymiarach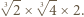
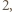 rozetniemy go na dwa przystające prostopadłościany o wymiarach
rozetniemy go na dwa przystające prostopadłościany o wymiarach 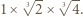 Każdy z nich jest podobny do
Każdy z nich jest podobny do 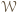 w skali
w skali 
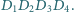 Niech
Niech 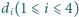 będzie odległością punktu
będzie odległością punktu 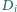 od płaszczyzny ustalonej podstawy graniastosłupa. Udowodnić, że
od płaszczyzny ustalonej podstawy graniastosłupa. Udowodnić, że
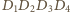 jest równoległobokiem i przesuń go tak, aby jego środek pokrył się ze środkiem podstawy.
jest równoległobokiem i przesuń go tak, aby jego środek pokrył się ze środkiem podstawy.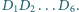 Niech
Niech 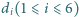 będzie odległością punktu
będzie odległością punktu 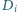 od płaszczyzny ustalonej podstawy graniastosłupa. Dowieść, że
od płaszczyzny ustalonej podstawy graniastosłupa. Dowieść, że
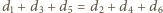 (wykorzystaj poprzednie zadanie).
(wykorzystaj poprzednie zadanie).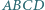 zachodzą równości:
zachodzą równości:
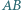 i
i 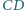 nie przekracza 4.
nie przekracza 4.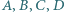 są takimi czterema wierzchołkami pewnego prostopadłościanu, że żadne dwa z nich nie są połączone krawędzią. Sfery
są takimi czterema wierzchołkami pewnego prostopadłościanu, że żadne dwa z nich nie są połączone krawędzią. Sfery 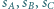 o środkach odpowiednio w punktach
o środkach odpowiednio w punktach 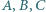 są parami styczne. Udowodnić, że istnieje sfera
są parami styczne. Udowodnić, że istnieje sfera 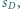 o środku w punkcie
o środku w punkcie 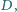 która jest styczna do sfer
która jest styczna do sfer 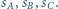
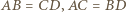 oraz
oraz 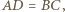 gdyż są to pary przekątnych przystających prostokątów.
gdyż są to pary przekątnych przystających prostokątów.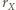 promień sfery
promień sfery 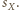 Jeżeli sfery
Jeżeli sfery 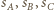 są parami styczne, to pewne dwie z nich - bez straty ogólności
są parami styczne, to pewne dwie z nich - bez straty ogólności 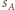 i
i 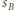 - są styczne zewnętrznie, czyli
- są styczne zewnętrznie, czyli 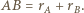 Jeśli
Jeśli 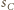 jest styczna zewnętrznie do
jest styczna zewnętrznie do 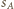 i
i 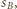 to
to 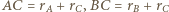 i wystarczy przyjąć
i wystarczy przyjąć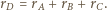
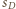 będzie styczna wewnętrznie do pozostałych trzech sfer, gdyż
będzie styczna wewnętrznie do pozostałych trzech sfer, gdyż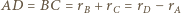

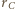 jest styczna wewnętrznie do
jest styczna wewnętrznie do 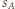 i
i 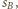 to
to
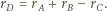
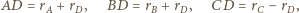
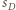 będzie styczna zewnętrznie do
będzie styczna zewnętrznie do 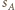 i
i 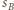 oraz styczna wewnętrznie do
oraz styczna wewnętrznie do