Cięcie piłą»Cięcie piłą
o zadaniu...
- Zadanie pochodzi z artykułu Dlaczego Martin Gardner był wielkim matematykiem, choć matematykiem nie był
- Publikacja w Delcie: styczeń 2011
- Publikacja elektroniczna: 18-12-2010
- Artykuł źródłowy w wersji do druku [application/pdf]: (146 KB)
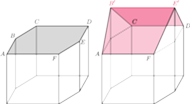
Jak wiadomo, sześcian dzieli się na 27 sześcianów o trzy razy krótszej krawędzi. Jaka jest najmniejsza liczba cięć, które pozwolą to zrealizować? Uzyskane w jakimś cięciu kawałki można ułożyć jedne na drugich i ciąć za jednym zamachem.
 (licząc
od wierzchołków) leżą na jednej sferze.
(licząc
od wierzchołków) leżą na jednej sferze.
 niech
niech
 będzie
środkiem sfery opisanej, a
będzie
środkiem sfery opisanej, a
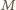 i
i
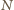 – środkami krawędzi
– środkami krawędzi
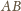 i
i
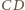 . Przez
. Przez
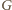 oznaczmy środek odcinka
oznaczmy środek odcinka
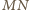 ,
czyli środek ciężkości czworościanu
,
czyli środek ciężkości czworościanu
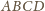 . Niech
. Niech
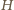 będzie
punktem symetrycznym do
będzie
punktem symetrycznym do
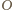 względem
względem
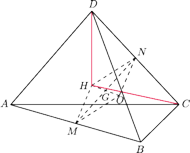
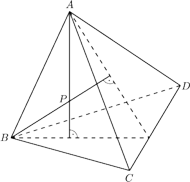
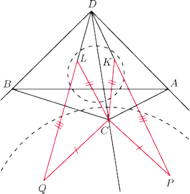
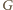 (rysunek). Punkty
(rysunek). Punkty
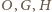 leżą wtedy na jednej prostej, a
leżą wtedy na jednej prostej, a
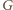 jest środkiem
odcinka
jest środkiem
odcinka
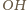 . Wobec tego chcemy wykazać, że
. Wobec tego chcemy wykazać, że
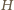 jest
ortocentrum czworościanu
jest
ortocentrum czworościanu
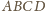 .
.
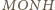 jest równoległobokiem.
W szczególności proste
jest równoległobokiem.
W szczególności proste
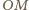 i
i
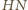 są równoległe. Z definicji
punktów
są równoległe. Z definicji
punktów
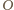 i
i
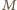 wynika, że odcinki
wynika, że odcinki
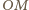 i
i
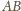 są
prostopadłe, więc również
są
prostopadłe, więc również
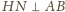 . Stąd i z prostopadłości
prostych
. Stąd i z prostopadłości
prostych
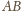 i
i
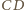 (
(
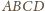 jest ortocentryczny!)
wynika, że płaszczyzna
jest ortocentryczny!)
wynika, że płaszczyzna
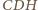 jest prostopadła do prostej
jest prostopadła do prostej
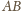 .
W takim razie prosta
.
W takim razie prosta
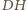 jest prostopadła do prostej
jest prostopadła do prostej
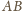 .
Analogicznie dowodzimy, że
.
Analogicznie dowodzimy, że
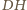 jest prostopadła również do
prostej
jest prostopadła również do
prostej
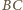 .
.
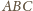 , czyli
stanowi wysokość czworościanu
, czyli
stanowi wysokość czworościanu
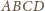 . Podobnie dowodzimy, że
proste
. Podobnie dowodzimy, że
proste
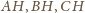 są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
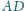 czworościanu
czworościanu
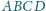 jest prostopadła do
płaszczyzny
jest prostopadła do
płaszczyzny
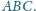 Wykazać, że rzut prostokątny ortocentrum
trójkąta
Wykazać, że rzut prostokątny ortocentrum
trójkąta
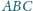 na płaszczyznę
na płaszczyznę
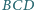 jest ortocentrum trójkąta
jest ortocentrum trójkąta
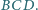
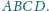 Dowieść, że krawędzie
Dowieść, że krawędzie
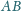 i
i
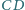 są prostopadłe wtedy i tylko wtedy, gdy istnieje w przestrzeni
taki równoległobok
są prostopadłe wtedy i tylko wtedy, gdy istnieje w przestrzeni
taki równoległobok
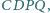 że
że
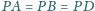 oraz
oraz
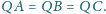
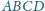 wysokości
poprowadzone z wierzchołków
wysokości
poprowadzone z wierzchołków
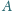 i
i
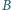 przecinają się, to również
wysokości poprowadzone z wierzchołków
przecinają się, to również
wysokości poprowadzone z wierzchołków
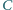 i
i
 przecinają
się.
przecinają
się.
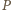 będzie punktem przecięcia wysokości czworościanu
poprowadzonych z wierzchołków
będzie punktem przecięcia wysokości czworościanu
poprowadzonych z wierzchołków
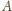 i
i
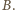 Mamy
Mamy
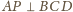 ,
więc też
,
więc też
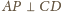 i analogicznie
i analogicznie
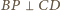 . W takim razie
płaszczyzna
. W takim razie
płaszczyzna
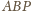 jest prostopadła do krawędzi
jest prostopadła do krawędzi
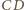 , w szczególności
, w szczególności
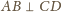 . Na prostej
. Na prostej
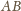 wybierzmy taki punkt
wybierzmy taki punkt
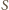 , że
, że
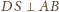 . Zatem płaszczyzna
. Zatem płaszczyzna
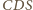 jest prostopadła do krawędzi
jest prostopadła do krawędzi
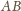 . Niech
. Niech
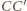 i
i
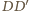 będą wysokościami trójkąta
będą wysokościami trójkąta
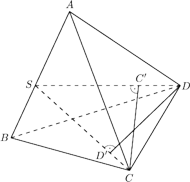
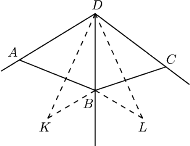
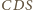 (rysunek obok). Prosta
(rysunek obok). Prosta
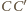 jest prostopadła zarówno
do
jest prostopadła zarówno
do
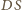 , jak i do
, jak i do
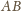 (bo leży w płaszczyźnie prostopadłej
do tej krawędzi). Jest więc wysokością czworościanu
(bo leży w płaszczyźnie prostopadłej
do tej krawędzi). Jest więc wysokością czworościanu
 poprowadzoną z wierzchołka
poprowadzoną z wierzchołka
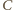 . Analogicznie dowodzimy, że również
. Analogicznie dowodzimy, że również
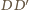 jest wysokością danego czworościanu. Te dwie proste mają punkt
wspólny będący ortocentrum trójkąta
jest wysokością danego czworościanu. Te dwie proste mają punkt
wspólny będący ortocentrum trójkąta
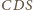 . Dowód jest więc
zakończony.
. Dowód jest więc
zakończony.
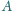 czworościanu
czworościanu
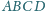 są proste. Wykazać, że rzut prostokątny
są proste. Wykazać, że rzut prostokątny
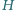 punktu
punktu
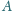 na
płaszczyznę
na
płaszczyznę
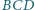 jest ortocentrum trójkąta
jest ortocentrum trójkąta
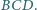
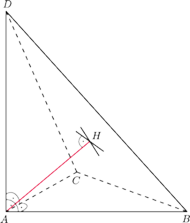
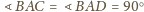 , to
, to
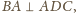 a więc
a więc
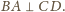 Ponadto
Ponadto
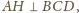 skąd
skąd
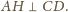 Zatem płaszczyzna
Zatem płaszczyzna
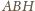 jest prostopadła do prostej
jest prostopadła do prostej
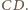 W takim razie
W takim razie
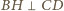 .
Analogicznie udowodnimy, że
.
Analogicznie udowodnimy, że
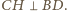 Zatem punkt
Zatem punkt
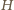 jest
ortocentrum trójkąta
jest
ortocentrum trójkąta
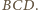
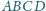 jest styczna do ściany
jest styczna do ściany
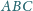 w punkcie
w punkcie
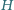 . Druga sfera jest styczna do ściany
. Druga sfera jest styczna do ściany
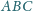 w punkcie
w punkcie
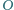 oraz jest styczna do płaszczyzn zawierających
pozostałe ściany tego czworościanu w punktach, które do czworościanu
nie należą. Wykaż, że jeżeli
oraz jest styczna do płaszczyzn zawierających
pozostałe ściany tego czworościanu w punktach, które do czworościanu
nie należą. Wykaż, że jeżeli
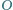 jest środkiem okręgu opisanego na
trójkącie
jest środkiem okręgu opisanego na
trójkącie
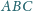 , to
, to
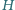 jest punktem przecięcia wysokości
tego trójkąta.
jest punktem przecięcia wysokości
tego trójkąta.
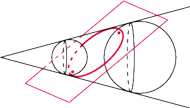
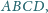 w którym
w którym
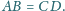 Sfera
wpisana w ten czworościan jest styczna do ścian
Sfera
wpisana w ten czworościan jest styczna do ścian
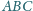 i
i
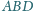 odpowiednio w punktach
odpowiednio w punktach
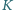 i
i
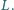 Dowieść, że jeżeli punkty
Dowieść, że jeżeli punkty
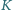 i
i
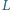 są środkami ciężkości ścian
są środkami ciężkości ścian
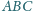 i
i
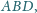 to czworościan
to czworościan
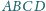 jest foremny.
jest foremny.
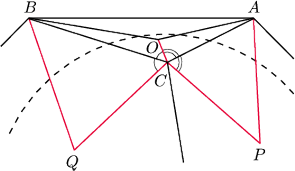
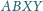 jest opisany na sferze. Punkty
jest opisany na sferze. Punkty
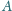 i
i
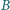 są
ustalone, a punkty
są
ustalone, a punkty
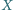 i
i
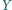 poruszają się. Udowodnić, że suma
kątów
poruszają się. Udowodnić, że suma
kątów

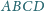 jest styczna do ściany
jest styczna do ściany
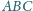 w punkcie
w punkcie
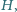 a sfera dopisana do tego czworościanu jest styczna do
ściany
a sfera dopisana do tego czworościanu jest styczna do
ściany
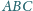 w punkcie
w punkcie
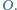 Dowieść, że jeżeli
Dowieść, że jeżeli
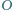 jest
środkiem okręgu opisanego na trójkącie
jest
środkiem okręgu opisanego na trójkącie
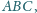 to
to
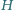 jest punktem
przecięcia wysokości tego trójkąta.
jest punktem
przecięcia wysokości tego trójkąta.
 i
i
 będą punktami styczności sfery wpisanej
w czworościan
będą punktami styczności sfery wpisanej
w czworościan
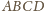 odpowiednio ze ścianami
odpowiednio ze ścianami
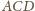 i
i
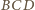 , a
, a
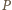 i
i
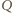 punktami styczności sfery dopisanej
odpowiednio z płaszczyznami
punktami styczności sfery dopisanej
odpowiednio z płaszczyznami
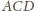 i
i
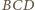 . Wówczas
trójkąty
. Wówczas
trójkąty
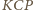 i
i
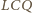 są przystające (
są przystające (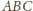 przy wierzchołkach
przy wierzchołkach
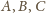 odpowiednio przez
odpowiednio przez
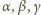 . Trójkąty
. Trójkąty
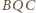 i
i
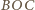 są
przystające, skąd wynika, że
są
przystające, skąd wynika, że
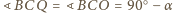 (
(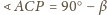 . Niech
. Niech
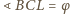 . Wtedy
. Wtedy
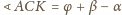 (bo
(bo
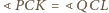 ). Jednakże
). Jednakże
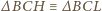 i
i
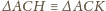 , więc
, więc
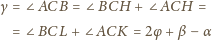
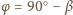 . Zatem
. Zatem
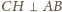 . Analogicznie
dowodzimy, że
. Analogicznie
dowodzimy, że
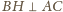 , a to oznacza, że
, a to oznacza, że
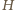 jest punktem
przecięcia wysokości trójkąta
jest punktem
przecięcia wysokości trójkąta
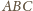 .
.
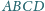 jest styczna do ścian
jest styczna do ścian
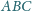 i
i
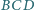 odpowiednio w punktach
odpowiednio w punktach
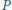 i
i
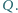 Dowieść, że
Dowieść, że
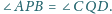
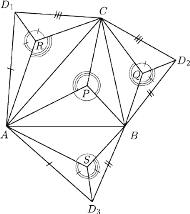
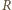 i
i
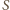 będą punktami styczności sfery wpisanej
odpowiednio ze ścianami
będą punktami styczności sfery wpisanej
odpowiednio ze ścianami
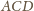 i
i
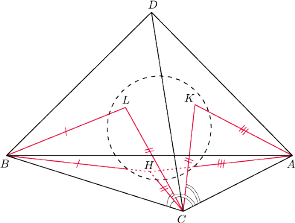
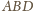 . Trójkąty utworzone przez
pewną krawędź i punkty styczności sfery wpisanej z dwoma ścianami
zawierającymi tę krawędź są przystające. Wygodnie jest teraz wszystko rysować
na siatce Oznaczmy:
. Trójkąty utworzone przez
pewną krawędź i punkty styczności sfery wpisanej z dwoma ścianami
zawierającymi tę krawędź są przystające. Wygodnie jest teraz wszystko rysować
na siatce Oznaczmy:
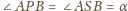 ,
,
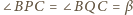 ,
,
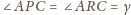 ,
,
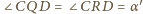 ,
,
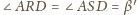 ,
,
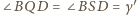 .
.

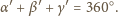
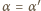 . Zatem
. Zatem
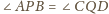 .
.
 ściany
ściany
 ).
).
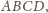 styczną do
ściany
styczną do
ściany
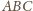 w punkcie
w punkcie
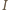 , który jest środkiem koła
wpisanego w trójkąt
, który jest środkiem koła
wpisanego w trójkąt
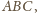 oraz styczną do płaszczyzn
oraz styczną do płaszczyzn
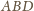 i
i
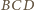 odpowiednio w punktach
odpowiednio w punktach
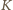 i
i
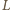 . Zauważmy, że
. Zauważmy, że
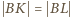 i
i
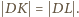
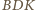 i
i
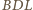 są przystające, a stąd
są przystające, a stąd
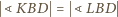
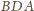 i
i
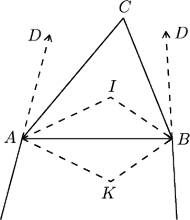
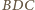 ,,rozłożone płasko”).
,,rozłożone płasko”).
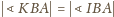 (rys.2) przedstawia
półpłaszczyzny
(rys.2) przedstawia
półpłaszczyzny
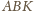 i
i
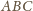 ,,rozłożone płasko”) – oraz że
,,rozłożone płasko”) – oraz że
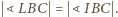
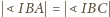 ; stąd
; stąd
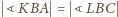 i w konsekwencji
i w konsekwencji
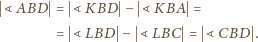
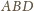 , stwierdzamy
analogicznie, że
, stwierdzamy
analogicznie, że
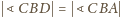 . Zatem wszystkie kąty płaskie ścian
przy wierzchołku
. Zatem wszystkie kąty płaskie ścian
przy wierzchołku
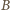 są równe:
są równe:
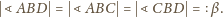
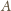 są równe (oznaczmy ich miarę przez
są równe (oznaczmy ich miarę przez
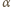 ), kąty przy wierzchołku
), kąty przy wierzchołku
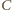 są równe
są równe
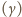 oraz kąty przy wierzchołku
oraz kąty przy wierzchołku
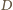 są równe
są równe
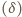 .
.
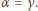 Analogicznie uzasadniamy, że
Analogicznie uzasadniamy, że
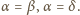 To znaczy, że wszystkie kąty
wszystkich ścian czworościanu są równe. Zatem ściany są trójkątami
równobocznymi i czworościan jest foremny.
To znaczy, że wszystkie kąty
wszystkich ścian czworościanu są równe. Zatem ściany są trójkątami
równobocznymi i czworościan jest foremny.