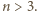w - k + s = 2»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu w - k + s = 2
- Publikacja w Delcie: marzec 2016
- Publikacja elektroniczna: 29 lutego 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (56 KB)
Czy istnieje wielościan wypukły, w którym 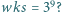
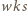 jest liczbą nieparzystą, to liczby
jest liczbą nieparzystą, to liczby 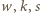 są nieparzyste, a więc niemożliwe, by
są nieparzyste, a więc niemożliwe, by 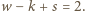
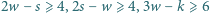 oraz
oraz 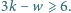
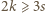 uzyskujemy
uzyskujemy 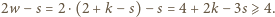 Pozostałych nierówności dowodzimy analogicznie.
Pozostałych nierówności dowodzimy analogicznie.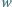 wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.
wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.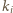 oznacza liczbę krawędzi ściany
oznacza liczbę krawędzi ściany 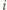 dla
dla 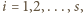 wówczas
wówczas 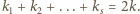 Suma kątów płaskich ścian wielościanu równa jest
Suma kątów płaskich ścian wielościanu równa jest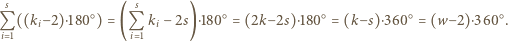
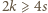 oraz
oraz 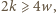 zatem
zatem 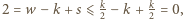 sprzeczność.
sprzeczność.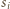 liczbę ścian
liczbę ścian 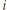 -kątnych, a przez
-kątnych, a przez 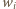 liczbę naroży
liczbę naroży 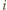 -ściennych
-ściennych 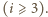
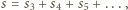
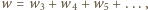
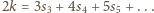 oraz
oraz 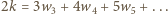 Stąd
Stąd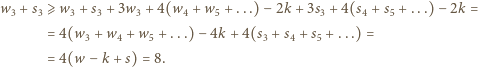
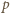 ścian pięciokątnych i
ścian pięciokątnych i 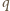 sześciokątnych, to
sześciokątnych, to 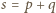 oraz
oraz 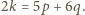 Wielokąty są foremne, zatem w każdym wierzchołku schodzą się po trzy. Stąd
Wielokąty są foremne, zatem w każdym wierzchołku schodzą się po trzy. Stąd 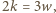 czyli
czyli 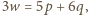 a więc
a więc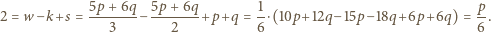
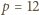 - wielościan ma 12 ścian pięciokątnych.
- wielościan ma 12 ścian pięciokątnych.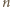 -kątów foremnych, po
-kątów foremnych, po 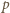 w każdym wierzchołku. Oznacza to, że
w każdym wierzchołku. Oznacza to, że 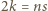 oraz
oraz 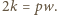 Wobec tego
Wobec tego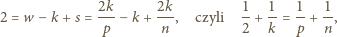
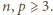 Równanie to ma pięć rozwiązań.
Równanie to ma pięć rozwiązań.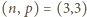 czworościan,
czworościan, 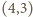 - sześcian,
- sześcian, 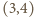 - ośmiościan,
- ośmiościan, 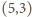 - dwunastościan i
- dwunastościan i 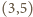 - dwudziestościan. Powyższe rozumowanie wskazuje, że więcej ich być nie może.
- dwudziestościan. Powyższe rozumowanie wskazuje, że więcej ich być nie może.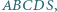 którego podstawą jest prostokąt
którego podstawą jest prostokąt 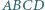 i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość
i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość 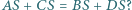 Odpowiedź uzasadnij.
Odpowiedź uzasadnij.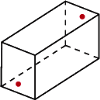
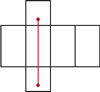
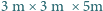 (
(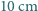 , siedzi pająk. Chce on dotrzeć do punktu położonego
, siedzi pająk. Chce on dotrzeć do punktu położonego 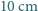 pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na
pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na 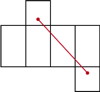

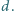 W wierzchołku
W wierzchołku 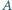 podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż
podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż 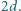

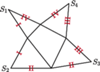
 z
z 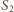 sklejają się w innym punkcie, niż
sklejają się w innym punkcie, niż 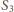 z
z 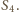 Wynika to z faktu, że na rysunku wysokości trójkątów, poprowadzone z wierzchołków
Wynika to z faktu, że na rysunku wysokości trójkątów, poprowadzone z wierzchołków 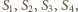 nie przecinają się w jednym punkcie - spodku wysokości ostrosłupa - a powinny.
nie przecinają się w jednym punkcie - spodku wysokości ostrosłupa - a powinny.
 o wszystkich bokach równej długości i kątach przy wierzchołkach
o wszystkich bokach równej długości i kątach przy wierzchołkach 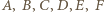 równych odpowiednio:
równych odpowiednio: 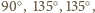
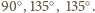 Niech
Niech 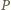 będzie punktem przecięcia przekątnych
będzie punktem przecięcia przekątnych 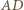 oraz
oraz 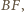 a
a 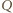 punktem przecięcia przekątnych
punktem przecięcia przekątnych 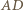 oraz
oraz 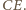 (
(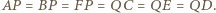 Wybierzmy teraz w przestrzeni punkty
Wybierzmy teraz w przestrzeni punkty 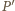 oraz
oraz 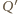 po tej samej stronie płaszczyzny sześciokąta, tak aby proste
po tej samej stronie płaszczyzny sześciokąta, tak aby proste 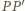 i
i 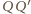 były prostopadłe do tej płaszczyzny oraz aby
były prostopadłe do tej płaszczyzny oraz aby 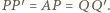 Wielościan
Wielościan 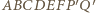 (
(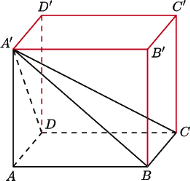
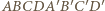 będzie prostopadłościanem. Wówczas ostrosłup
będzie prostopadłościanem. Wówczas ostrosłup 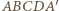 spełnia warunki zadania.
spełnia warunki zadania.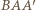 oraz
oraz 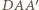 są, oczywiście, prostokątne. Ponadto, ponieważ prosta
są, oczywiście, prostokątne. Ponadto, ponieważ prosta 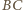 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 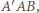 to jest ona prostopadła do każdej prostej z tej płaszczyzny, w szczególności do prostej
to jest ona prostopadła do każdej prostej z tej płaszczyzny, w szczególności do prostej 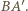 Zatem trójkąt
Zatem trójkąt 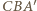 jest prostokątny. Podobnie dowodzimy, że trójkąt
jest prostokątny. Podobnie dowodzimy, że trójkąt 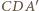 jest prostokątny.
jest prostokątny.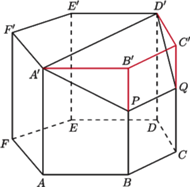
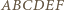 oraz
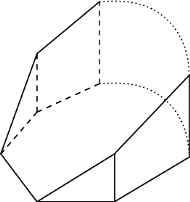
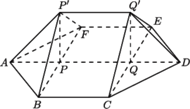
oraz 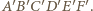 Graniastosłup ten ma 18 krawędzi i wszystkie jego ściany mają parzystą liczbę boków. Gdyby udało się dodać jedną krawędź, nie zmieniając własności ścian, to otrzymany wielościan spełniałby warunki zadania. Zauważmy, że sześciokąt
Graniastosłup ten ma 18 krawędzi i wszystkie jego ściany mają parzystą liczbę boków. Gdyby udało się dodać jedną krawędź, nie zmieniając własności ścian, to otrzymany wielościan spełniałby warunki zadania. Zauważmy, że sześciokąt 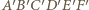 można bez trudu podzielić jedną z przekątnych na dwa czworokąty. Teraz tylko trzeba zrobić z tych czworokątów ściany wielościanu przez pochylenie jednego z nich. Poprowadźmy więc przez punkty
można bez trudu podzielić jedną z przekątnych na dwa czworokąty. Teraz tylko trzeba zrobić z tych czworokątów ściany wielościanu przez pochylenie jednego z nich. Poprowadźmy więc przez punkty 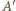 oraz
oraz 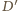 płaszczyznę przecinającą krawędzie
płaszczyznę przecinającą krawędzie 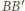 i
i 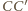 odpowiednio w punktach
odpowiednio w punktach 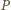 oraz
oraz 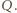 Płaszczyzna ta dzieli graniastosłup na dwa wielościany, z których jeden spełnia warunki zadania: ma osiem ścian będących czworokątami i jedną ścianę sześciokątną. Ponadto wielościan ten ma
Płaszczyzna ta dzieli graniastosłup na dwa wielościany, z których jeden spełnia warunki zadania: ma osiem ścian będących czworokątami i jedną ścianę sześciokątną. Ponadto wielościan ten ma 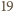 krawędzi.
krawędzi.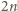 -kątem, dla
-kątem, dla