Geometria Bolyaia–Łobaczewskiego

Najdłużej badanym problemem matematycznym była kwadratura koła. Zaraz za nią uplasowała się kwestia piątego postulatu Euklidesa. Chodziło o to, czy zdanie "jeśli dwie proste przecięte trzecią tworzą kąty wewnętrzne jednostronne o sumie mniejszej od dwóch kątów prostych, to proste te po przedłużeniu przetną się i to właśnie z tej strony" spełnia wymagane dla postulatów warunki, czyli czy wyraża rzeczy jasne i oczywiste i czy jest dostatecznie zwięzłe, by być uznane za pierwotną prawdę. Debatę zapoczątkował w V wieku Proklos, odpowiadając dwukrotnie nie i proponując, by wykazać, że usunięcie tego postulatu gmachu geometrii nie naruszy.

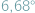 względem kierunku prostopadłego do płaszczyzny jego okołoziemskiej orbity (Księżyc orbituje w płaszczyźnie, która z kolei przecina ekliptykę pod kątem
względem kierunku prostopadłego do płaszczyzny jego okołoziemskiej orbity (Księżyc orbituje w płaszczyźnie, która z kolei przecina ekliptykę pod kątem 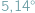 ). Jako że okres rotacji Księżyca wokół osi jest zsynchronizowany z okresem orbitalnym (miesiącem księżycowym), widzimy zawsze tę samą, upstrzoną kraterami i ciemnymi plamami (morzami, maria, które w istocie są bazaltowymi równinami) stronę satelity...
). Jako że okres rotacji Księżyca wokół osi jest zsynchronizowany z okresem orbitalnym (miesiącem księżycowym), widzimy zawsze tę samą, upstrzoną kraterami i ciemnymi plamami (morzami, maria, które w istocie są bazaltowymi równinami) stronę satelity...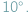 Jak co roku, główną atrakcją sierpnia są promieniujące już od lipca meteory z roju Perseidów. Są to szybkie meteory, ich prędkość zderzenia z atmosferą Ziemi wynosi 59 km/s i często zostawiają za sobą smugi dymu, powoli rozwiewające się w powietrzu.
Jak co roku, główną atrakcją sierpnia są promieniujące już od lipca meteory z roju Perseidów. Są to szybkie meteory, ich prędkość zderzenia z atmosferą Ziemi wynosi 59 km/s i często zostawiają za sobą smugi dymu, powoli rozwiewające się w powietrzu.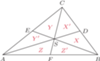
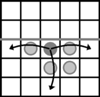
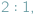 licząc od wierzchołka trójkąta (rys. obok).
licząc od wierzchołka trójkąta (rys. obok).