Zadanie ZM-1575
o zadaniu...
- Publikacja w Delcie: sierpień 2018
- Publikacja elektroniczna: 31 lipca 2018
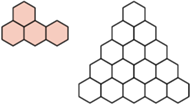
Płytką nazwiemy pokazaną na rysunku figurę złożoną z czterech sześciokątów foremnych o boku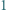 
oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei 
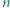-trójkątem nazwiemy trójkątny układ tworzony przez 
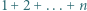sześciokątów foremnych o boku 
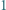(na rysunku pokazano 
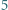-trójkąt). Znaleźć wszystkie dodatnie liczby całkowite 
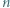o tej własności, że z pewnej liczby płytek można ułożyć 
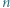-trójkąt.
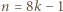lub 
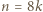dla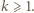 
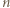-trójkąt można ułożyć z płytek, to jest on złożony z podzielnej przez 
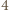liczby sześciokątów foremnych o boku 
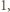co oznacza, że liczba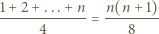
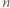daje resztę 0 lub 
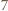przy dzieleniu przez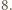 
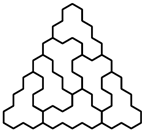
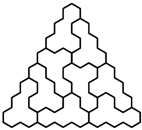
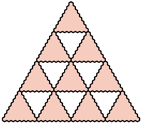
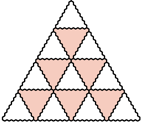
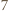-trójkąt oraz 
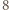-trójkąt można ułożyć z płytek. Ponadto dla każdego 
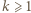z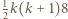 
-trójkątów oraz 
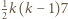-trójkątów można ułożyć 
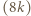-trójkąt, a z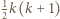 
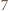-trójkątów oraz 
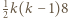-trójkątów można ułożyć 
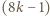-trójkąt (rysunki 3 i 4; 
).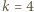