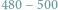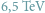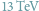20 III, od godziny 23:45, nareszcie astronomiczna wiosna!

Jakiś czas temu (Delta 11/2012) zwróciliśmy uwagę na nowy typ bardzo jasnych źródeł rentgenowskich, odkrytych w galaktykach M31 i M83. Ilość promieniowania tych obiektów jest w trakcie przejściowych pojaśnień o wiele większa niż przewidywana przez standardowy model cienkiego dysku akrecyjnego...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Odklejanie etykiet z cenami lub kodami paskowymi w taki sposób, by nie pozostawiły po sobie żadnych śladów, jest jedną z tych czynności, które potrafią doprowadzić do stanu irytacji niemal każdego. Co ciekawe, niezależnie od stopnia zdeterminowania jednostki, by - mierząc się z takim wyzwaniem - zachować spokój i pełną kontrolę nad wykonywanymi ruchami, przebieg jej zmagań na ogół odtwarza ten sam uniwersalny schemat, po którym zamiast słodyczy długo oczekiwanego zwycięstwa należy spodziewać się raczej goryczy kolejnej porażki...

Emitery światła oparte na azotku galu (GaN) rewolucjonizują codzienne życie. Dzięki niebieskim laserom azotkowym Blu-ray czterokrotnie zwiększyła się gęstość optycznego zapisu danych. Gdy włączamy telewizor, cieszy nas wysoka jakość obrazu i odwzorowanie kolorów, możliwe dzięki nowoczesnym wyświetlaczom z podświetleniem diodowym. Od kilku lat powszechne stają się mikroprojektory, oparte na bardzo jasnych, półprzewodnikowych źródłach światła. Poszerzają się też możliwości diagnostyki medycznej czy komunikacji podwodnej dzięki laserom emitującym światło zielone nm. Wszystko to zawdzięczamy kryształowi azotku galu, który określany jest jako półprzewodnik przyszłości.

Żeby zrozumieć coś z zachodzących w świecie procesów, należy to i owo pomierzyć. Żeby odkryć coś nowego - trzeba wykonać pomiar i uzasadnić, że nie zgadza się on z istniejącą wiedzą. Jednak wykonywanie pomiarów na granicy możliwości doświadczalnych to nie taka prosta sprawa.

Przygotowania biegną zgodnie z planem. Schłodzony już został hel, i to aż do nadciekłości (styczeń 2015), w największej i najzimniejszej lodówce znanego wszechświata. Pierwsze wiązki protonów o energii spodziewane są tuż po ukazaniu się tego numeru Delty, a pierwsze zderzenia przy mają zajść dwa miesiące później.

W tym kąciku omówimy zadanie Filary, które pojawiło się na Akademickich Mistrzostwach Polski w Programowaniu Zespołowym 2014. Zadanie, pomimo prostej treści i (jak się za chwilę przekonamy) całkiem prostego rozwiązania, sprawiło sporo kłopotów drużynom startującym w zawodach i ostatecznie zostało rozwiązane tylko przez jedną z nich.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W dniach 24-26 października 2014 roku odbyła się kolejna - siódma już - konferencja organizowana przez Stowarzyszenie na rzecz Edukacji Matematycznej. Konferencja była okazją do spotkania się osób z różnych środowisk zaangażowanych w edukację matematyczną, popularyzację matematyki i pracę z młodzieżą uzdolnioną matematycznie.

Rozpowszechnione jest przeświadczenie, że znaczna część dowodów geometrycznych prowadzonych przez mędrców Złotego Wieku Grecji, a więc czasów po zwycięskich wojnach perskich i kojarzących się nam np. z Peryklesem, wyglądała tak, iż był to rysunek ze słownym komentarzem: Patrz. Niezależnie od podziwu dla intelektualnej estetyki takich dowodów podejrzewamy, że dotyczyły one problemów mało skomplikowanych, rozumowań wymagających jednego kroku myślowego.

Istnieje zaskakujący związek między okręgiem wpisanym w trójkąt i okręgiem na nim opisanym.

W pewnym mieście podjęto decyzję o budowie nowego osiedla. Postanowiono, że będzie to szereg ośmiu budynków. Przyjęto, że żadne trzy stojące obok siebie budynki nie mogą być tej samej wysokości. Ustalono, że budynki będą mieć wysokości równe odpowiednio: 5, 10, 10, 15, 25, 25, 30 i 45 metrów...

Najbardziej zachęcającym aspektem uprawiania matematyki (oczywiście, poza niezaprzeczalnym pięknem matematycznych teorii) jest jej szeroka gama zastosowań i olbrzymia efektywność w modelowaniu świata rzeczywistego. Popularne jest nawet określenie "niepojęta skuteczność matematyki" (np. w pracy E. Wignera pod tożsamym tytułem The Unreasonable Effectiveness of Mathematics in the Natural Sciences). Warto jednak pamiętać, że modelowanie matematyczne jest czymś więcej niż tylko wyjątkowo użytecznym młotkiem wbijającym kolejne gwoździe, na których opiera się nasze zrozumienie wszechświata. Dzięki matematyce możemy modelować nie tylko to, co jest rzeczywiste (w jakimkolwiek tego słowa znaczeniu), ale też wszystko, co tylko potrafimy sobie wyobrazić.

...jeden lepiej, a drugi trochę gorzej... co jest lekko zmienionym świetnym tekstem Jonasza Kofty o śpiewaniu. Rzeczywiście, władza ludowa wypleniła w Polsce zjawisko analfabetyzmu i wydawało się, że odtąd wystarczy już wydawać gazety i książki i cały naród (teraz się mówi "społeczeństwo") będzie wiedział wszystko, co należy. Jeżeli były też jakieś wiadomości mniej zalecane, to jeszcze były wydawnictwa drugiego obiegu i nadal życie społeczeństwa biegło w porządku właściwego uświadomienia.

Na brzegu Dzikiej Orlicy, w wiosce Helvíkovice, która dziś jest przedmieściem Žamberku, stoi niewielki dom, wybudowany w stylu charakterystycznym dla regionu Gór Orlickich. Urodził się w nim wynalazca Wacław Divíšek, który na kartach nauki zapisał się jako Prokop Diviš (1698 -1765). Kiedy po śmierci ojca gospodarstwo objął jego starszy brat, dzięki pomocy pochodzącego z Žamberku rektora szkoły Henryka Dušíka, chłopiec nie został, na przykład, pomocnikiem cieśli albo kowala, ale rozpoczął naukę w jezuickim kolegium w Znojmie. Wstąpił do zakonu norbertanów i uczył się dalej, obronił doktoraty z teologii oraz z filozofii w Salzburgu i w Ołomuńcu. Jednak pasją jego życia stały się nauki przyrodnicze.