Dowody „just-do-it” w zadaniach o przeliczalności
W zeszłym roku (już po raz drugi!) miałem przyjemność pełnić funkcję tutora podczas obozu Maths Beyond Limits. Poprowadziłem dwie serie zajęć, z których jedna dotyczyła teorii mnogości. Starając się dać uczestnikom podstawy arytmetyki zbiorów nieskończonych w zajmujący i bezbolesny, mam nadzieję, sposób, pokazałem ciekawe zadania, wykorzystujące różne metody i pomysły. Jeden z nich jest szczególnie warty uwagi...
Zadając proste pytanie "Czy istnieje zbiór […] spełniający warunki […]?", można wygenerować wiele zadań. Niektórzy nawet zaznaczą, że przeliczalnie wiele. Struktura zbiorów jest na tyle prosta, że jeśli rozwiązanie istnieje (i przypadkiem nie jest równoważne hipotezie continuum), prawdopodobnie znajdziemy je, korzystając z podstawowych własności funkcji działających na zbiorach. Dodatkowo, czasem warto przeformułować problem, powiązać go z czymś dobrze znanym, pozwalającym lepiej go zwizualizować (np. myśleć o podzbiorach płaszczyzny zamiast o całej płaszczyźnie). Dobrym planem ataku może być więc nie próba znalezienia abstrakcyjnego dowodu, a konstrukcja przykładu metodą just-do-it! Jeżeli zbiór rzeczywiście istnieje, być może nie będzie trudno go znaleźć. Jeżeli zaś pomysły (bądź nerwy) wyczerpią się, można spróbować dowieść jego nieistnienia.
Metodę just-do-it dobrze promuje na swoim blogu Medalista Fieldsa, Tim Gowers, poprzez następujące zadanie:
Zadanie. Czy istnieje gęsty podzbiór płaszczyzny, który nie zawiera trzech współliniowych punktów?
Istnienie takiego zbioru byłoby raczej zaskakujące, mając na uwadze, że zbiory gęste są w pewnym sensie duże (w odniesieniu do zbioru, w którym są gęste), natomiast brak trzech współliniowych punktów sugeruje, że zbiór powinien być mały. Wszelkie wątpliwości znikną jednak, gdy zastosujemy podejście just-do-it. Oczywiście zachęcam Czytelnika do próby samodzielnego rozwiązania przed przejściem do dalszej części tekstu.
Spróbujmy zatem ów zbiór skonstruować. Oznaczmy go przez 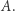 Wiemy, że zbiór punktów o współrzędnych
Wiemy, że zbiór punktów o współrzędnych 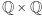 jest gęsty na płaszczyźnie. Zauważmy, że wystarczy pokazać gęstość zbioru
jest gęsty na płaszczyźnie. Zauważmy, że wystarczy pokazać gęstość zbioru 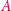 względem zbioru
względem zbioru 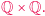 Zamiast analizować całą płaszczyznę na raz, rozważmy jej mniejsze kawałki: kule otwarte
Zamiast analizować całą płaszczyznę na raz, rozważmy jej mniejsze kawałki: kule otwarte 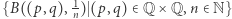 o środkach w punktach
o środkach w punktach 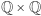 i promieniach
i promieniach 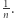 Czyli dla każdego punktu z
Czyli dla każdego punktu z 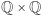 rozważmy przeliczalnie wiele kul (mogą mieć dowolnie mały promień). Przeformułujmy zadanie następująco:
rozważmy przeliczalnie wiele kul (mogą mieć dowolnie mały promień). Przeformułujmy zadanie następująco:
Zadanie. Dany jest przeliczalny zbiór kul otwartych 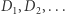 Czy istnieje zbiór
Czy istnieje zbiór 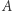 (podzbiór
(podzbiór 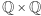 ) taki, że
) taki, że 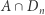 jest niepusty dla każdego
jest niepusty dla każdego 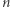 i żadne trzy punkty z
i żadne trzy punkty z 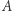 nie leżą na jednej prostej?
nie leżą na jednej prostej?
Zbiór 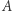 skonstruujemy indukcyjnie. Niech
skonstruujemy indukcyjnie. Niech 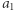 będzie dowolnym punktem z
będzie dowolnym punktem z 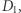 natomiast
natomiast 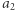 dowolnym punktem z
dowolnym punktem z 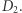 Dalej, wybierzmy
Dalej, wybierzmy 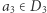 takie, że nie leży ono na prostej zawierającej
takie, że nie leży ono na prostej zawierającej 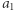 i
i 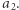 Kuli otwartej nie da się pokryć skończoną liczbą prostych, zatem na pewno istnieje odpowiednie
Kuli otwartej nie da się pokryć skończoną liczbą prostych, zatem na pewno istnieje odpowiednie 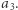 Tę konstrukcję można kontynuować, co daje finalne rozwiązanie.
Tę konstrukcję można kontynuować, co daje finalne rozwiązanie.
Okazuje się zatem, że nasza konstrukcja sprowadza się do kilku pomysłów, które można uogólnić do całej klasy zadań tego typu. Po pierwsze, skorzystaliśmy z faktu, że zbiór 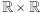 ma przeliczalny podzbiór gęsty (jest ośrodkowy). Pozwoliło nam to sprowadzić problem do podobnego, prawie że skończonego i umożliwiło konstrukcję krok po kroku. Jedyne, co pozostało, to zacisnąć zęby i dokończyć rozumowanie.
ma przeliczalny podzbiór gęsty (jest ośrodkowy). Pozwoliło nam to sprowadzić problem do podobnego, prawie że skończonego i umożliwiło konstrukcję krok po kroku. Jedyne, co pozostało, to zacisnąć zęby i dokończyć rozumowanie.
Podczas moich zajęć wiele zadań można było rozwiązać, korzystając z podobnego rozumowania. Na przykład:
Zadanie. Czy istnieje nieprzeliczalny zbiór parami rozłącznych bałwanków na płaszczyźnie?
Nie można zapomnieć, że funkcje w pewnym sensie są także zbiorami, czyli że o 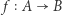 można myśleć jako o podzbiorze
można myśleć jako o podzbiorze 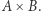 Możemy zatem mieć nadzieję, że pytania o istnienie funkcji o określonych własnościach można rozwiązywać podobnie. Warto przyjrzeć się następującemu zadaniu:
Możemy zatem mieć nadzieję, że pytania o istnienie funkcji o określonych własnościach można rozwiązywać podobnie. Warto przyjrzeć się następującemu zadaniu:
Zadanie. Wykazać, że dla każdej funkcji 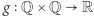 istnieje funkcja
istnieje funkcja 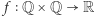 taka, że
taka, że 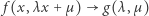 przy
przy 
W przypadku problemów, wystarczy przypomnieć sobie przytoczone rozumowanie i... Just do it!
Tłumaczyli Anna ŁEŃ (MISMaP UW) oraz Paweł PIWEK (Uniwersytet Cambridge)
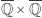 jest podzbiorem gęstym płaszczyzny. Jeżeli z tego zbioru wyrzucimy punkt o współrzędnych
jest podzbiorem gęstym płaszczyzny. Jeżeli z tego zbioru wyrzucimy punkt o współrzędnych 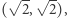 to zbiór nadal będzie gęsty.
to zbiór nadal będzie gęsty.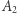 jest gęsty w zbiorze
jest gęsty w zbiorze 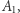 a
a 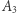 jest gęsty w zbiorze
jest gęsty w zbiorze 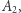 to z tego wynika, że
to z tego wynika, że 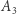 jest gęsty w
jest gęsty w 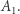
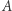 jest gęstym podzbiorem płaszczyzny: w dowolnym zbiorze otwartym można umieścić któryś ze zbiorów
jest gęstym podzbiorem płaszczyzny: w dowolnym zbiorze otwartym można umieścić któryś ze zbiorów 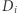 (dowolnie mała kula), a z nim zbiór
(dowolnie mała kula), a z nim zbiór 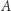 ma na pewno co najmniej jeden punkt wspólny.
ma na pewno co najmniej jeden punkt wspólny.