Zbiór

Zbiór to najbardziej podstawowe pojęcie matematyki. Ze zbiorami mamy do czynienia właściwie we wszystkich dyscyplinach matematycznych. Choć każdy Czytelnik na pewno intuicyjnie rozumie słowo "zbiór" (np. jako kolekcję lub zestaw utworzony z pewnego rodzaju elementów), to pojęcie to nie ma formalnej definicji.

Do zdefiniowania dowolnego terminu zawsze potrzebujemy użyć jakiegoś innego pojęcia. Podczas studiów matematycznych każdy student usłyszy, że przestrzeń metryczna to zbiór, w którym zdefiniowano funkcję odległości o odpowiednich własnościach. Słyszy też, że grupa to zbiór, na którym zdefiniowano operację mnożenia spełniającą określone warunki. Zbiór jest pojęciem pierwotnym, nie ma więc swojej definicji - nie ma innego pojęcia, na którym tę definicję można by oprzeć. Każdy Czytelnik zna jednak wiele przykładów zbiorów, takich jak zbiór liczb naturalnych 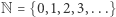$N = {0,1,2,3,...}$ czy też zbiór wszystkich egzemplarzy tego numeru Delty. Jest też specjalny zbiór, w którym nie ma żadnych elementów, nazywany zbiorem pustym i oznaczany $|∅.$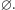

Zbiory jednak nie mają nieograniczonej dowolności w swoim istnieniu. Muszą spełniać aksjomaty, czyli zdania opisujące ich podstawowe własności (stanowiące w pewnym sensie definicję tego pojęcia). Na przykład jeden z aksjomatów mówi, że jeśli dwa zbiory mają takie same elementy, to te zbiory są sobie równe (inaczej mówiąc, patrzymy wtedy na jeden i ten sam zbiór). Inny aksjomat postuluje, że dla każdego zbioru istnieje zbiór jego podzbiorów. 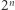Łatwo można wysnuć wniosek, że podzbiorów zbioru $n$ -elementowego jest $2n$ - wyjaśnienie w Kąciku Młodego Olimpijczyka.

Zauważmy także, że nie wszystkie koncepty, którym chcemy przypisać własność zbioru, istnieją. Na przykład nie istnieje "zbiór wszystkich zbiorów". Widać, że w szczególności taki zbiór musiałby być swoim elementem, co już jest niepokojące. Załóżmy mimo wszystko istnienie "zbioru wszystkich zbiorów" i rozważmy jego podzbiór 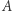$|A$ złożony ze wszystkich zbiorów, które nie są własnymi elementami. Zastanówmy się, czy 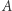$A |$ należy do samego siebie. Jeśli tak, to 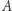$|A$ nie należy do 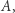$A, |$ bo nie spełnia warunku definiującego ten zbiór. Jeśli nie, to 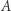$A |$ należy do 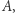$A, |$ bo ten warunek spełnia. Ale to jest sprzeczność.