Dwa dowody jednego twierdzenia
Zbiór wszystkich liczb rzeczywistych 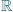 nie jest równoliczny ze zbiorem wszystkich liczb naturalnych
nie jest równoliczny ze zbiorem wszystkich liczb naturalnych 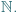
Przypomnijmy: zbiory 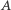 i
i 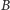 są równoliczne, gdy istnieje funkcja różnowartościowa z
są równoliczne, gdy istnieje funkcja różnowartościowa z 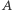 na
na 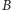 (lub - równoważnie - z
(lub - równoważnie - z 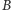 na
na 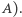
Twierdzenie. Zbiór wszystkich liczb rzeczywistych 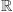 nie jest równoliczny ze zbiorem wszystkich liczb naturalnych
nie jest równoliczny ze zbiorem wszystkich liczb naturalnych 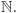
Dowód przekątniowy
Gwoli jednoznaczności przyjmijmy, że każdą niezerową liczbę z przedziału ![|[0, 1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/1x-e1fda79bf71eedae21d61308c0ba9defb0ae3a4b-im-33,33,33-FF,FF,FF.gif) reprezentujemy przez jej rozwinięcie dziesiętne, w którym jest nieskończenie wiele cyfr niezerowych (a więc, na przykład, 1/4 jest reprezentowana przez
reprezentujemy przez jej rozwinięcie dziesiętne, w którym jest nieskończenie wiele cyfr niezerowych (a więc, na przykład, 1/4 jest reprezentowana przez 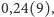 a nie
a nie 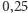 ). Wówczas każda liczba rzeczywista z przedziału
). Wówczas każda liczba rzeczywista z przedziału ![|[0,1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/4x-e1fda79bf71eedae21d61308c0ba9defb0ae3a4b-im-33,33,33-FF,FF,FF.gif) ma dokładnie jedną reprezentację dziesiętną. Niech
ma dokładnie jedną reprezentację dziesiętną. Niech ![| f N [0,1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/5x-e1fda79bf71eedae21d61308c0ba9defb0ae3a4b-im-33,33,33-FF,FF,FF.gif) będzie dowolną funkcją z
będzie dowolną funkcją z 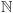 w przedział domknięty
w przedział domknięty ![|[0, 1],](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/7x-e1fda79bf71eedae21d61308c0ba9defb0ae3a4b-im-33,33,33-FF,FF,FF.gif) czyli ciągiem o wyrazach rzeczywistych należących do tego przedziału, i niech
czyli ciągiem o wyrazach rzeczywistych należących do tego przedziału, i niech 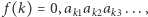 gdzie
gdzie 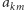 oznacza
oznacza  -tą cyfrę po przecinku liczby
-tą cyfrę po przecinku liczby 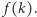 Niech dalej
Niech dalej

Wówczas liczba 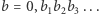 należy do przedziału
należy do przedziału ![[0,1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/14x-e1fda79bf71eedae21d61308c0ba9defb0ae3a4b-im-33,33,33-FF,FF,FF.gif) i nie jest wyrazem ciągu
i nie jest wyrazem ciągu 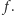 Rzeczywiście:
Rzeczywiście: 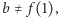 bo
bo 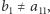 podobnie
podobnie 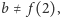 bo
bo 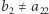 i tak dalej. Ogólniej, dla każdej liczby naturalnej
i tak dalej. Ogólniej, dla każdej liczby naturalnej 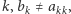 co oznacza, że
co oznacza, że 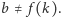
Wobec dowolności wyboru funkcji 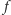 możemy stwierdzić, że nie istnieje funkcja z
możemy stwierdzić, że nie istnieje funkcja z 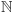 w
w ![|[0,1],](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/3x-c73778e85cc8f06fa2dce831987ec42cadbe1ec3-im-33,33,33-FF,FF,FF.gif) której zbiór wartości wyczerpywałby przedział
której zbiór wartości wyczerpywałby przedział ![|[0, 1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/4x-c73778e85cc8f06fa2dce831987ec42cadbe1ec3-im-33,33,33-FF,FF,FF.gif) ; tym bardziej nie istnieje funkcja z
; tym bardziej nie istnieje funkcja z 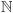 na całe
na całe 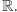
Dowód analityczny
Jak poprzednio, niech ![f N [0,1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/1x-029b826b37e5af4bc5b303d1fb6de2245f977dfd-im-33,33,33-FF,FF,FF.gif) będzie dowolną funkcją z
będzie dowolną funkcją z 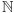 w przedział domknięty
w przedział domknięty ![[0,1],](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/3x-029b826b37e5af4bc5b303d1fb6de2245f977dfd-im-33,33,33-FF,FF,FF.gif) czyli ciągiem o wyrazach rzeczywistych należących do tego przedziału.
czyli ciągiem o wyrazach rzeczywistych należących do tego przedziału.
Niech 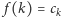 dla
dla 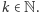 Podzielmy przedział
Podzielmy przedział ![[0,1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/3x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) na trzy domknięte podprzedziały o długości 1/3 każdy i niech
na trzy domknięte podprzedziały o długości 1/3 każdy i niech ![[a ,b ] 0 0](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/4x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) będzie takim z nich, do którego nie należy
będzie takim z nich, do którego nie należy 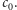 Tak więc
Tak więc ![1 |[a0,b0] ⊂ [0, 1],b0 −a0 = 3](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/6x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![|c0 /∈ [a0,b0].](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/7x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) Załóżmy, że dla
Załóżmy, że dla 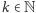 zdefiniowaliśmy już przedział
zdefiniowaliśmy już przedział ![|[ak, bk]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/9x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) tak, że
tak, że ![[ak,bk] ⊂ [0,1],bk − ak = 31k 1](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/10x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) oraz
oraz ![ck /∈ [ak,bk].](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/11x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) Wówczas dzielimy przedział
Wówczas dzielimy przedział ![|[a ,b ] k k](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/12x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) na trzy domknięte podprzedziały równej długości i definiujemy
na trzy domknięte podprzedziały równej długości i definiujemy ![|[ak+1,bk+1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/13x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) jako ten podprzedział, do którego nie należy
jako ten podprzedział, do którego nie należy 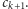 Mamy wtedy:
Mamy wtedy:
![--1- [ak+1,bk+1]⊂ [ak,bk], bk+1− ak+1 = 3k+2 oraz ck+1 /∈ [ak+1,bk+1].](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/15x-c30fac757bcb54b747dc3145277d7155fa13f5f2-dm-33,33,33-FF,FF,FF.gif)
W ten sposób na mocy indukcji otrzymujemy taki ciąg przedziałów ![|[a ,b ], n n](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/16x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) że dla każdej liczby naturalnej
że dla każdej liczby naturalnej 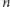
![[an+1,bn+1]⊂ [an,bn] ⊂[0,1], bn − an =--1- oraz cn /∈ [an,bn]. 3n+1](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/18x-c30fac757bcb54b747dc3145277d7155fa13f5f2-dm-33,33,33-FF,FF,FF.gif)
Ciąg 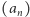 jest niemalejący i ograniczony z góry przez 1, ciąg
jest niemalejący i ograniczony z góry przez 1, ciąg 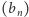 jest nierosnący i ograniczony z dołu przez 0, zatem oba te ciągi są zbieżne i mają wspólną granicę, gdyż ciąg
jest nierosnący i ograniczony z dołu przez 0, zatem oba te ciągi są zbieżne i mają wspólną granicę, gdyż ciąg 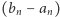 dąży do 0; nazwijmy ją
dąży do 0; nazwijmy ją 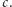 Ponadto dla każdej liczby naturalnej
Ponadto dla każdej liczby naturalnej ![n, c∈ [a ,b ], n n](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/23x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) podczas gdy
podczas gdy ![|cn /∈ [an, bn].](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/24x-c30fac757bcb54b747dc3145277d7155fa13f5f2-im-33,33,33-FF,FF,FF.gif) Wniosek:
Wniosek: 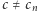 dla każdego
dla każdego 
Tak więc nie istnieje funkcja z 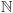 w
w ![[0,1],](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/2x-ec632f632a8c371e47ee9c62151db022c722fb03-im-33,33,33-FF,FF,FF.gif) której zbiór wartości wyczerpywałby przedział
której zbiór wartości wyczerpywałby przedział ![[0,1]](/math/temat/matematyka/analiza/2017/03/26/Dwa_dowody_jednego_twierdzenia/3x-ec632f632a8c371e47ee9c62151db022c722fb03-im-33,33,33-FF,FF,FF.gif) ; tym bardziej nie istnieje funkcja z
; tym bardziej nie istnieje funkcja z 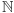 na całe
na całe