Przesuwanie w zadaniach olimpijskich»Zadanie 6
o zadaniu...
- Zadanie olimpijskie: I etap 53 OM
- Zadanie pochodzi z artykułu Przesuwanie w zadaniach olimpijskich
- Publikacja w Delcie: luty 2018
- Publikacja elektroniczna: 1 lutego 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (87 KB)
Płaszczyzna przecina krawędzie boczne graniastosłupa prawidłowego sześciokątnego, tworząc w przekroju sześciokąt wypukły 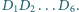 Niech
Niech 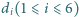 będzie odległością punktu
będzie odległością punktu 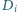 od płaszczyzny ustalonej podstawy graniastosłupa. Dowieść, że
od płaszczyzny ustalonej podstawy graniastosłupa. Dowieść, że

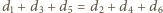 (wykorzystaj poprzednie zadanie).
(wykorzystaj poprzednie zadanie).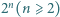 znajdują się punkty
znajdują się punkty 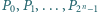 będące wierzchołkami
będące wierzchołkami 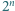 -kąta foremnego, oznaczone w taki sposób, że długość łuku
-kąta foremnego, oznaczone w taki sposób, że długość łuku 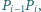 mierzonego zgodnie z ruchem wskazówek zegara, jest równa
mierzonego zgodnie z ruchem wskazówek zegara, jest równa 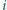 dla każdego
dla każdego 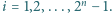 Niech
Niech
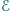 i
i 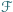 są przystające (jako podzbiory płaszczyzny).
są przystające (jako podzbiory płaszczyzny).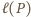 będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego
będzie długością łuku (mierzoną zgodnie z ruchem wskazówek zegara) łączącego 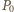 z
z 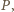 tzn. dla każdego
tzn. dla każdego 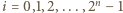
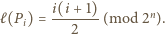
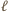 jest bijekcją zbioru wierzchołków
jest bijekcją zbioru wierzchołków 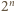 -kąta i
-kąta i ![|Z ∩ [0,2n −1].](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/30/zm-1530/8x-5a02d8212f68e6296da2e894dc2a3a250bf72f4c-im-66,57,43-FF,FF,FF.gif)
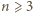 zachodzi równość
zachodzi równość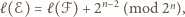
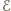 jest obrazem
jest obrazem 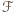 przy obrocie o
przy obrocie o 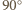 wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego
wokół środka danego okręgu zgodnie z ruchem wskazówek zegara. Konkretnie, wykażemy, że dla każdego 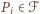
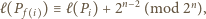
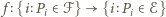 określona jest następująco
określona jest następująco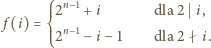
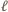 wystarczy więc sprawdzić, że dla każdego
wystarczy więc sprawdzić, że dla każdego 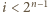 liczba
liczba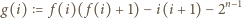
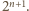 Rzeczywiście, bezpośrednio z definicji funkcji
Rzeczywiście, bezpośrednio z definicji funkcji 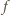 otrzymujemy, że jeżeli
otrzymujemy, że jeżeli 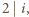 to
to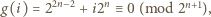
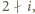 to
to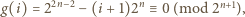
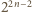 dzieli się przez
dzieli się przez 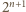 dla
dla 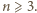 Pozostaje bezpośrednio sprawdzić, że dla
Pozostaje bezpośrednio sprawdzić, że dla 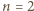 rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o
rozważane zbiory także są przystające (odpowiednia izometria znów jest obrotem o 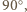 ale w przeciwną stronę).
ale w przeciwną stronę).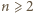 istnieje etykietowanie wierzchołków
istnieje etykietowanie wierzchołków 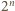 -kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie
-kąta foremnego o opisanych własnościach - jest to równoważne zadaniu 2 z I etapu LX OM, którego rozwiązanie można znaleźć na stronie 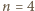 z zaznaczonymi zbiorami
z zaznaczonymi zbiorami 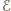 oraz
oraz 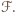
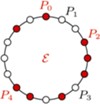
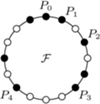
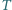 rozcięto wzdłuż odcinka na dwa trójkąty
rozcięto wzdłuż odcinka na dwa trójkąty 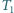 i
i 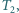 a trójkąt
a trójkąt 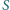 - na trójkąty
- na trójkąty 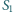 i
i 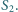 Okazało się, że trójkąt
Okazało się, że trójkąt 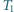 jest przystający do trójkąta
jest przystający do trójkąta 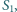 a trójkąt
a trójkąt 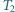 jest przystający do trójkąta
jest przystający do trójkąta 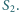 Czy wynika z tego, że trójkąty
Czy wynika z tego, że trójkąty 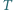 i
i 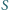 są przystające?
są przystające?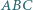 i
i 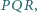 przy czym
przy czym 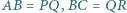 oraz
oraz 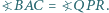 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?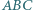 i
i 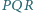 mają równe pola oraz
mają równe pola oraz 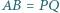 i
i 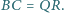 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?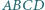 i
i 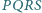 mają równe pola oraz
mają równe pola oraz 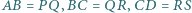 i
i 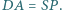 Czy wynika z tego, że czworokąty te są przystające?
Czy wynika z tego, że czworokąty te są przystające?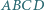 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 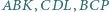 i
i 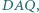 pierwsze dwa z nich na zewnątrz czworokąta, pozostałe dwa - do wewnątrz. Wykaż, że
pierwsze dwa z nich na zewnątrz czworokąta, pozostałe dwa - do wewnątrz. Wykaż, że 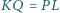 oraz
oraz 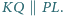

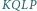
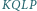
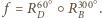 Na mocy
Na mocy 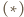 jest to przesunięcie, ponadto
jest to przesunięcie, ponadto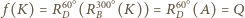
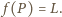 Oznacza to, że
Oznacza to, że 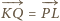 (jest to wektor przesunięcia
(jest to wektor przesunięcia 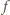 ), co kończy dowód.
), co kończy dowód.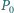 i trójkąt
i trójkąt 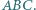 Niech
Niech 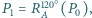
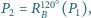
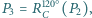
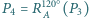 itd. Udowodnij, że jeżeli
itd. Udowodnij, że jeżeli 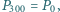 to trójkąt
to trójkąt 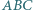 jest równoboczny.
jest równoboczny.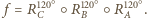 Na mocy
Na mocy 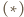 jest to przesunięcie. Z treści zadania wynika, że
jest to przesunięcie. Z treści zadania wynika, że 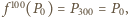 stąd wektor przesunięcia jest zerowy, czyli
stąd wektor przesunięcia jest zerowy, czyli 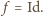 Wobec tego na mocy
Wobec tego na mocy 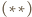 trójkąt
trójkąt 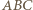 ma kąty równe
ma kąty równe 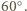
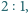 licząc od wierzchołka.
licząc od wierzchołka.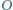 jest środkiem elipsy wpisanej w czworokąt
jest środkiem elipsy wpisanej w czworokąt 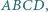 to
to
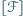 oznacza pole figury
oznacza pole figury 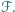
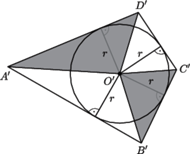
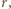 obrazem punktu
obrazem punktu 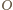 jest środek okręgu
jest środek okręgu 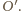 Czworokąt
Czworokąt 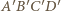 jest opisany na okręgu, zachodzi więc równość
jest opisany na okręgu, zachodzi więc równość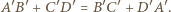
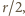 uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.
uzyskujemy tezę dla okręgu. Przekształcenia afiniczne zachowują równość pól, zatem teza zachodzi także dla wyjściowej elipsy.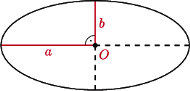
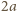 i
i 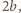 równoległych do jej półosi. Powinowactwo prostokątne o skali
równoległych do jej półosi. Powinowactwo prostokątne o skali 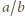 i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola
i o osi zawierającej dużą półoś elipsy przekształca nasz prostokąt na kwadrat, a elipsę na koło weń wpisane. Stąd stosunek pola 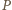 elipsy do pola
elipsy do pola 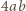 prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli
prostokąta równy jest stosunkowi pola koła do pola kwadratu na nim opisanego, czyli 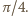 Wobec tego
Wobec tego 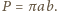
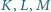 leżą odpowiednio na bokach
leżą odpowiednio na bokach 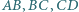 równoległoboku
równoległoboku 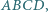 przy czym
przy czym
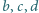 przechodzą odpowiednio przez punkty
przechodzą odpowiednio przez punkty 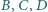 oraz są równoległe odpowiednio do prostych
oraz są równoległe odpowiednio do prostych 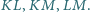 Udowodnij, że proste
Udowodnij, że proste  przecinają się w jednym punkcie.
przecinają się w jednym punkcie.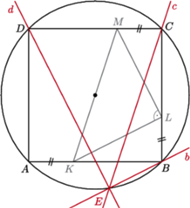
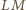 powstaje z odcinka
powstaje z odcinka 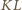 przez obrót o
przez obrót o 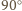 wokół środka kwadratu, zatem
wokół środka kwadratu, zatem 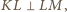 więc także
więc także 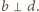 Stąd punkt
Stąd punkt 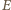 przecięcia prostych
przecięcia prostych 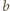 i
i 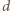 leży na okręgu opisanym na kwadracie. Ponadto skoro
leży na okręgu opisanym na kwadracie. Ponadto skoro 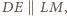 to punkt
to punkt 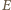 musi należeć do tego łuku
musi należeć do tego łuku 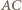 okręgu, który zawiera
okręgu, który zawiera 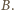 Wobec tego
Wobec tego 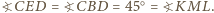 Na mocy
Na mocy 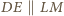 wynika stąd, iż
wynika stąd, iż 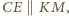 czyli
czyli 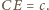 Zatem proste
Zatem proste 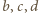 przecinają się w jednym punkcie
przecinają się w jednym punkcie 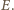
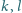 są styczne do okręgu
są styczne do okręgu
 w punktach
w punktach
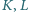 i przecinają
się w punkcie
i przecinają
się w punkcie
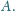 Punkt
Punkt
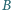 jest środkiem odcinka
jest środkiem odcinka
 Wykazać, że punkty
Wykazać, że punkty
 są symetryczne względem okręgu
są symetryczne względem okręgu
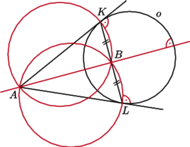
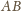 jest prostopadła do
jest prostopadła do
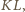 to jako bloki z definicji
można przyjąć okręgi o średnicach
to jako bloki z definicji
można przyjąć okręgi o średnicach
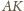 i
i
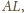 gdyż są
prostopadłe do
gdyż są
prostopadłe do
 i przechodzą przez
i przechodzą przez
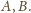 Oczywiście, sama
prosta
Oczywiście, sama
prosta
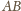 też się do tego celu nadaje.
też się do tego celu nadaje.
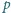 i
i
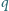 przecinają się w punktach
przecinają się w punktach
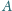 i
i
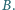 Prosta
Prosta
 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
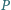 i
i
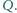 Punkt
Punkt
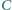 jest środkiem odcinka
jest środkiem odcinka
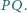 Wykazać,
że punkty
Wykazać,
że punkty
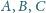 są współliniowe.
są współliniowe.

 będzie okręgiem o średnicy
będzie okręgiem o średnicy
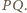 Okręgi
Okręgi
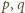 są
do niego prostopadłe, a zatem punkty
są
do niego prostopadłe, a zatem punkty
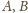 są symetryczne względem
są symetryczne względem
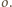 Stąd już wynika, że są współliniowe z punktem
Stąd już wynika, że są współliniowe z punktem
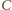 jako
środkiem tego okręgu – prosta poprowadzona z
jako
środkiem tego okręgu – prosta poprowadzona z
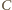 do punktu
do punktu
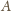 jest prostopadła do
jest prostopadła do
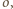 więc musi przechodzić przez punkt
więc musi przechodzić przez punkt
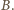
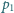 i
i
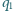 przecinają się w punktach
przecinają się w punktach
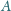 i
i
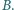 Prosta
Prosta
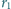 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
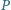 i
i
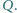 Punkt
Punkt
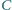 jest symetryczny do punktu
jest symetryczny do punktu
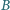 względem prostej
względem prostej
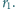 Okrąg
Okrąg
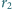 jest opisany na trójkącie
jest opisany na trójkącie
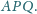 Proste
Proste
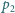 i
i
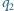 styczne do
styczne do
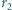 w punktach
odpowiednio
w punktach
odpowiednio
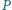 i
i
 przecinają się w punkcie
przecinają się w punkcie
 Wykazać,
że punkty
Wykazać,
że punkty
 są współliniowe.
są współliniowe.
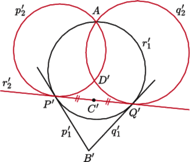
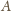 ; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
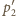 i
i
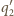 przecinają się w punktach
przecinają się w punktach
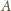 i
i
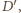 prosta
prosta
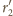 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach
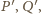 okrąg
okrąg
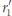 jest opisany na trójkącie
jest opisany na trójkącie
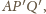 proste
proste
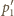 i
i
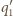 są styczne do
są styczne do
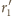 w punktach
w punktach
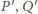 oraz
przecinają się w punkcie
oraz
przecinają się w punkcie
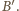
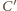 jest symetryczny do punktu
jest symetryczny do punktu
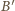 względem okręgu
względem okręgu
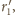 co na mocy zadania 1 oznacza, że jest
środkiem odcinka
co na mocy zadania 1 oznacza, że jest
środkiem odcinka
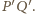 W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
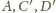 są współliniowe. Obrazem prostej
są współliniowe. Obrazem prostej
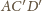 jest prosta
jest prosta
 co kończy rozwiązanie.
co kończy rozwiązanie.
 i
i
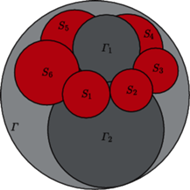
 są styczne wewnętrznie do sfery
są styczne wewnętrznie do sfery
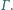 Do każdej z tych trzech sfer styczna jest każda z
Do każdej z tych trzech sfer styczna jest każda z
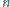 sfer
sfer
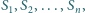 ponadto dla każdego
ponadto dla każdego
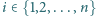 sfera
sfera
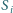 styczna jest do sfery
styczna jest do sfery
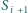 (przy czym
(przy czym
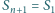 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch sfer
istnieje taki łańcuch sfer
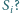 W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
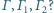 Czy i jak zależy to
od wyboru początkowej sfery
Czy i jak zależy to
od wyboru początkowej sfery
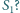
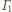 i
i
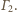 Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
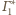 i
i
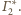 Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
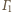 i
i
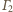 jest
środek inwersji.
jest
środek inwersji.
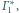
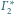
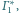
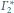
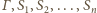 jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
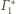 i
i
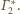 Z równoległości tych płaszczyzn wynika, że wszystkie sfery
Z równoległości tych płaszczyzn wynika, że wszystkie sfery
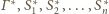 mają średnice równe odległości
mają średnice równe odległości
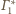 od
od
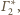 czyli są przystające. Ponadto wszystkie sfery
czyli są przystające. Ponadto wszystkie sfery
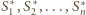 są
styczne do sfery
są
styczne do sfery
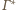 oraz dla każdego
oraz dla każdego
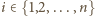 sfera
sfera
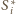 styczna jest do sfery
styczna jest do sfery
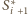 (przy czym
(przy czym
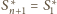 ).
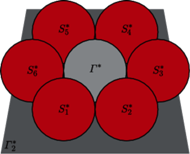
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
).
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
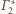 ) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
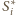 otacza środkową
piłeczkę
otacza środkową
piłeczkę
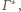 stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
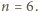
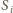 ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
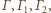 ani też od wyboru sfery
ani też od wyboru sfery
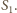 Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
 Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery
Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery
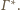
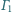 i
i
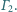 Do
każdego z nich styczny jest każdy z
Do
każdego z nich styczny jest każdy z
 okręgów
okręgów
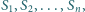 ponadto
dla każdego
ponadto
dla każdego
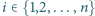 okrąg
okrąg
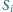 styczny jest do okręgu
styczny jest do okręgu
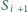 (przy czym
(przy czym
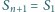 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch
okręgów
istnieje taki łańcuch
okręgów
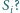 W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
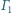 i
i
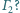 Czy i jak zależy to od wyboru
początkowego okręgu
Czy i jak zależy to od wyboru
początkowego okręgu
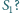
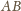 kwadratu to część prostej
kwadratu to część prostej
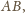 zawarta w kącie
zawarta w kącie