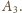Obroty w zadaniach geometrycznych»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu Obroty w zadaniach geometrycznych
- Publikacja w Delcie: październik 2004
- Publikacja elektroniczna: 16-02-2011
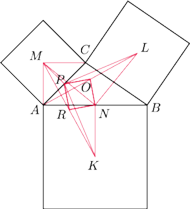
Punkty
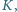
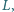
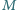 są środkami kwadratów zbudowanych
zewnętrznie na bokach
są środkami kwadratów zbudowanych
zewnętrznie na bokach
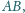
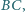
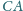 trójkąta
trójkąta
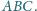 Wykazać, że
Wykazać, że
- (a)
- odcinki
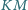 i
i
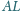 są prostopadłe,
są prostopadłe,
- (b)
- środki odcinków
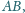
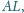
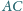 i
i
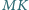 są
wierzchołkami kwadratu.
są
wierzchołkami kwadratu.
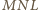 jest prostokątnym
trójkątem równoramiennym, przy czym
jest prostokątnym
trójkątem równoramiennym, przy czym
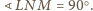 Zauważmy, że
Zauważmy, że
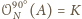 oraz
oraz
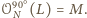 Tak więc
Tak więc
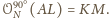 W szczególności odcinki
W szczególności odcinki
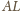 i
i
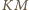 są prostopadłe.
są prostopadłe.
 wiemy, że
wiemy, że
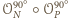 jest symetrią
środkową
jest symetrią
środkową
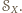 Ponieważ
Ponieważ
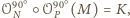 więc
środek
więc
środek
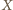 tej symetrii pokrywa się ze środkiem
tej symetrii pokrywa się ze środkiem
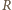 odcinka
odcinka
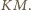 Ponadto z
Ponadto z
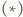 wynika również, że
wynika również, że
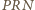 jest
prostokątnym trójkątem równoramiennym. Z zadania 4 wynika, że
jest
prostokątnym trójkątem równoramiennym. Z zadania 4 wynika, że
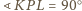 oraz
oraz
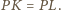 Tak więc
Tak więc
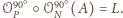 Stąd
Stąd
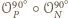 jest symetrią środkową względem środka
jest symetrią środkową względem środka
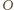 odcinka
odcinka
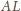 oraz tak jak poprzednio
oraz tak jak poprzednio
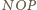 jest prostokątnym
trójkątem równoramiennym. Ostatecznie czworokąt
jest prostokątnym
trójkątem równoramiennym. Ostatecznie czworokąt
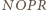 jest
kwadratem.
jest
kwadratem.
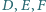 leżą odpowiednio na bokach
leżą odpowiednio na bokach
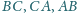 trójkąta
trójkąta
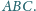 Okręgi wpisane w trójkąty
Okręgi wpisane w trójkąty
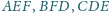 są
styczne do okręgu wpisanego w trójkąt
są
styczne do okręgu wpisanego w trójkąt
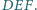 Udowodnij, że proste
Udowodnij, że proste
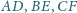 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
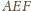 i
i
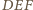 są styczne wtedy i tylko
wtedy, gdy w czworokąt
są styczne wtedy i tylko
wtedy, gdy w czworokąt
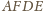 można wpisać okrąg.
można wpisać okrąg.
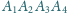 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku
 Punkty
Punkty
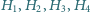 to ortocentra trójkątów, odpowiednio,
to ortocentra trójkątów, odpowiednio,
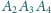 ,
,
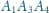 ,
,
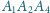 ,
,
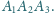 Wykaż, że czworokąty
Wykaż, że czworokąty
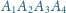 i
i
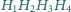 są przystające.
są przystające.
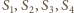 będą środkami ciężkości odpowiednio
powyższych czterech trójkątów,
będą środkami ciężkości odpowiednio
powyższych czterech trójkątów,
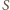 zaś – środkiem ciężkości
czwórki punktów
zaś – środkiem ciężkości
czwórki punktów
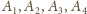 . Z własności środków ciężkości,
dla każdego
. Z własności środków ciężkości,
dla każdego
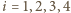 punkty
punkty
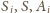 leżą, w tej
właśnie kolejności, na jednej prostej oraz
leżą, w tej
właśnie kolejności, na jednej prostej oraz
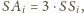 zatem
zatem
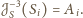 Z twierdzenia o prostej Eulera, dla każdego
Z twierdzenia o prostej Eulera, dla każdego
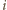 punkty
punkty
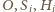 leżą, w tej właśnie kolejności, na jednej prostej oraz
leżą, w tej właśnie kolejności, na jednej prostej oraz
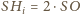 , stąd
, stąd
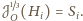 Złożenie
Złożenie
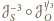 to
jednokładność o skali
to
jednokładność o skali
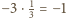 (symetria środkowa), która
przeprowadza
(symetria środkowa), która
przeprowadza
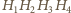 na
na
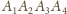 . Zatem czworokąty te są
przystające.
. Zatem czworokąty te są
przystające.

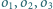 są styczne odpowiednio do par boków
są styczne odpowiednio do par boków
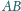 i
i
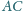 ,
,
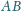 i
i
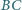 oraz
oraz
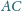 i
i
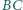 trójkąta
trójkąta
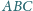 .
Okrąg
.
Okrąg
 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów
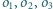 odpowiednio w punktach
odpowiednio w punktach
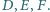 Wykaż, że proste
Wykaż, że proste
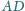 ,
,
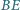 ,
,
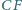 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
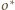 będzie okręgiem wpisanym w trójkąt
będzie okręgiem wpisanym w trójkąt
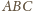 . Istnieje
. Istnieje
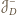 taka, że
taka, że
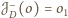 , oraz
, oraz
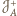 taka, że
taka, że
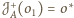 ,
wtedy
,
wtedy
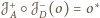 . Złożenie
. Złożenie
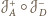 jest więc jednokładnością
odwrotną, przeprowadzającą
jest więc jednokładnością
odwrotną, przeprowadzającą
 na
na
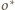 (istnieje dokładnie
jedna, nawet jeśli
(istnieje dokładnie
jedna, nawet jeśli
 i
i
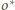 są przystające lub równe). Stąd jej
środek leży na prostej
są przystające lub równe). Stąd jej
środek leży na prostej
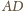 . Analogicznie, leży też na prostych
. Analogicznie, leży też na prostych
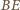 i
i
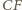 .
.
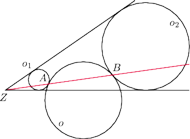
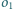 i
i
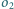 są rozłączne zewnętrznie i wpisane w kąt
o wierzchołku
są rozłączne zewnętrznie i wpisane w kąt
o wierzchołku
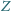 . Okrąg
. Okrąg
 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów
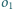 i
i
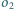 odpowiednio w punktach
odpowiednio w punktach
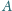 i
i
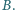 Udowodnij,
że punkty
Udowodnij,
że punkty
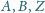 są współliniowe.
są współliniowe.
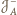 i
i
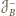 takie, że
takie, że
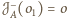 oraz
oraz
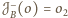 . Jednokładność
. Jednokładność
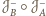 jest prosta oraz
jest prosta oraz
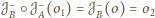 , więc jej środkiem musi być punkt
, więc jej środkiem musi być punkt
 .
Leży on zatem na prostej
.
Leży on zatem na prostej
 .
.
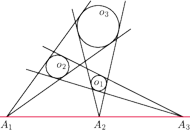
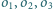 są rozłączne zewnętrznie. Te dwie styczne do
są rozłączne zewnętrznie. Te dwie styczne do
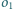 i
i
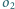 , które nie rozdzielają tych okręgów, przecinają się
w punkcie
, które nie rozdzielają tych okręgów, przecinają się
w punkcie
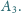 Analogicznie definiujemy punkty
Analogicznie definiujemy punkty
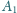 i
i
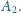 Wykaż, że punkty
Wykaż, że punkty
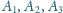 są współliniowe.
są współliniowe.
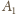 ,
,
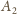 i
i
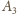 są środkami jednokładności
są środkami jednokładności
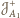 ,
,
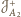 i
i
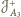 takich, że
takich, że
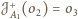 ,
,
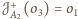 oraz
oraz
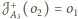 . Złożenie
. Złożenie
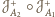 to jednokładność
prosta i
to jednokładność
prosta i
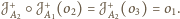 Stąd jej środkiem, który
na mocy twierdzenia musi leżeć na prostej
Stąd jej środkiem, który
na mocy twierdzenia musi leżeć na prostej
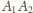 , jest na mocy faktu
punkt
, jest na mocy faktu
punkt