W krzywym zwierciadle»Zadanie 2
o zadaniu...
- Zadanie olimpijskie: XLVIII Olimpiada Matematyczna
- Zadanie pochodzi z artykułu W krzywym zwierciadle
- Publikacja w Delcie: maj 2013
- Publikacja elektroniczna: 30-04-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (68 KB)
Okrąg o środku w punkcie
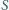 i wpisany w czworokąt wypukły
i wpisany w czworokąt wypukły
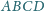 jest styczny do boków
jest styczny do boków
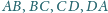 odpowiednio
w punktach
odpowiednio
w punktach
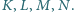 Proste
Proste
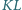 i
i
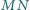 przecinają
się w punkcie
przecinają
się w punkcie
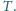 Wykaż, że proste
Wykaż, że proste
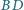 i
i
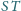 są
prostopadłe.
są
prostopadłe.

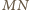 w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
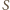 i przez stałe
punkty
i przez stałe
punkty
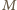 i
i
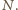 Leży na nim też punkt
Leży na nim też punkt
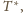 bo
punkt
bo
punkt
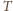 leży na prostej
leży na prostej
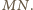 Średnicą tego okręgu jest
Średnicą tego okręgu jest
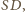 ponieważ kąty
ponieważ kąty
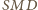 i
i
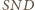 są proste, stąd także
są proste, stąd także
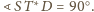
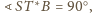 więc
więc
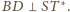 Z definicji inwersji
punkty
Z definicji inwersji
punkty
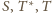 są współliniowe, co kończy dowód.
są współliniowe, co kończy dowód.

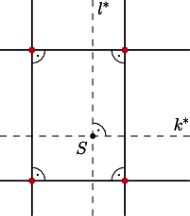
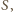 przy oznaczeniach jak na rysunku. Proste
przy oznaczeniach jak na rysunku. Proste
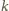 i
i
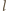 są stałe
przy tej inwersji. Obrazem każdego z okręgów, przechodzącego przez środek
inwersji, jest prosta równoległa odpowiednio do
są stałe
przy tej inwersji. Obrazem każdego z okręgów, przechodzącego przez środek
inwersji, jest prosta równoległa odpowiednio do
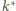 lub
lub
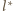 (okrąg
styczny do prostej
(okrąg
styczny do prostej
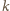 lub
lub
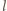 mieści się w półpłaszczyźnie przez
nią wyznaczonej, więc jego obraz też, rysunek obok). Zatem obrazami
kolorowych punktów są wierzchołki prostokąta. Leżą one na okręgu
nieprzechodzącym przez środek inwersji (bo środek ten jest wewnątrz
prostokąta), więc także przed inwersją kolorowe punkty leżą na jednym
okręgu.
mieści się w półpłaszczyźnie przez
nią wyznaczonej, więc jego obraz też, rysunek obok). Zatem obrazami
kolorowych punktów są wierzchołki prostokąta. Leżą one na okręgu
nieprzechodzącym przez środek inwersji (bo środek ten jest wewnątrz
prostokąta), więc także przed inwersją kolorowe punkty leżą na jednym
okręgu.
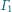 i
i
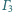 jest styczny zewnętrznie
do każdego z rozłącznych okręgów
jest styczny zewnętrznie
do każdego z rozłącznych okręgów
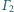 i
i
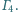 Wykaż, że punkty
styczności leżą na jednym okręgu.
Wykaż, że punkty
styczności leżą na jednym okręgu.
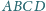 okręgi wpisane w trójkąty
okręgi wpisane w trójkąty
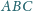 i
i
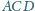 są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
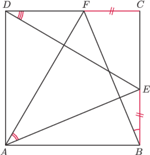
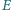 i
i
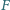 leżą odpowiednio na bokach
leżą odpowiednio na bokach
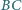 i
i
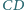 kwadratu
kwadratu
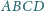 o boku 1, przy czym
o boku 1, przy czym
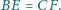 Udowodnij, że
Udowodnij, że
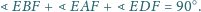
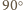 wokół środka. Obrazem trójkąta
wokół środka. Obrazem trójkąta
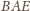 jest trójkąt
jest trójkąt
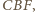 zatem
zatem
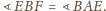 Analogicznie
Analogicznie
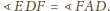 Stąd
Stąd
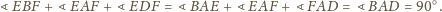
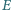 i
i
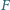 leżą odpowiednio na bokach
leżą odpowiednio na bokach
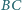 i
i
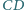 kwadratu
kwadratu
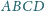 o boku 1, przy czym
o boku 1, przy czym
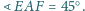 Wykaż, że
Wykaż, że
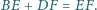
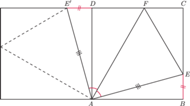
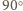 wokół wierzchołka
wokół wierzchołka
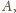 niech
niech
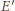 będzie obrazem punktu
będzie obrazem punktu
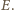 Wtedy
Wtedy
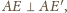 zatem
zatem
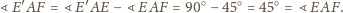
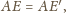 więc
więc
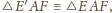 bo trójkąty te mają
dodatkowo wspólny bok
bo trójkąty te mają
dodatkowo wspólny bok
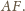 Stąd
Stąd
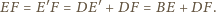
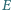 i
i
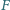 leżą odpowiednio na bokach
leżą odpowiednio na bokach
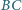 i
i
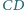 kwadratu
kwadratu
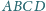 o boku 1, przy czym obwód
trójkąta
o boku 1, przy czym obwód
trójkąta
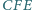 równy jest 2. Wyznacz miarę kąta
równy jest 2. Wyznacz miarę kąta
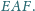
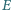 i
i
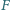 leżą odpowiednio na bokach
leżą odpowiednio na bokach
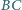 i
i
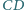 kwadratu
kwadratu
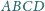 o boku 1, przy czym
o boku 1, przy czym
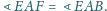 Wykaż, że
Wykaż, że
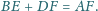
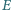 i
i
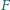 leżą odpowiednio na bokach
leżą odpowiednio na bokach
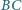 i
i
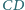 kwadratu
kwadratu
 o boku 1, przy czym
o boku 1, przy czym
 Oblicz wysokość trójkąta
Oblicz wysokość trójkąta
 poprowadzoną
z wierzchołka
poprowadzoną
z wierzchołka
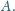
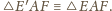 Wysokości tych
trójkątów poprowadzone z wierzchołka
Wysokości tych
trójkątów poprowadzone z wierzchołka
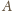 są więc obie równe
są więc obie równe
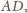 czyli 1.
czyli 1.
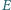 i
i
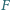 leżą odpowiednio na bokach
leżą odpowiednio na bokach
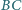 i
i
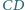 kwadratu
kwadratu
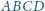 o boku 1, przy czym
o boku 1, przy czym
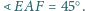 Proste
Proste
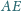 i
i
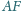 przecinają przekątną
przecinają przekątną
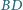 odpowiednio w punktach
odpowiednio w punktach
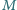 i
i
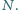 Proste
Proste
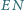 i
i
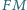 przecinają się w punkcie
przecinają się w punkcie
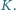 Wykaż, że proste
Wykaż, że proste
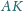 i
i
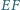 są prostopadłe.
są prostopadłe.
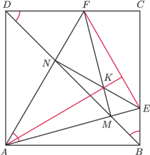
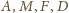 leżą na jednym okręgu, bo
leżą na jednym okręgu, bo
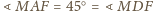 i punkty
i punkty
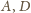 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej
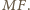 Kąt
Kąt
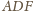 jest
prosty, więc
jest
prosty, więc
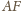 jest średnicą tego okręgu. Stąd
jest średnicą tego okręgu. Stąd
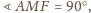 zatem
zatem
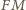 jest wysokością trójkąta
jest wysokością trójkąta
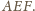 Analogicznie
Analogicznie
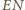 jest
wysokością tego trójkąta, więc
jest
wysokością tego trójkąta, więc
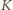 to jego ortocentrum. Wobec tego
to jego ortocentrum. Wobec tego
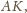 jako trzecia wysokość, jest prostopadła do
jako trzecia wysokość, jest prostopadła do
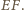
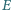 i
i
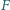 leżą odpowiednio na bokach
leżą odpowiednio na bokach
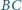 i
i
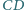 kwadratu
kwadratu
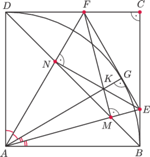
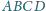 o boku 1, przy czym prosta
o boku 1, przy czym prosta
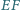 jest styczna do okręgu o środku
jest styczna do okręgu o środku
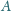 i promieniu 1. Proste
i promieniu 1. Proste
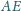 i
i
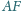 przecinają przekątną
przecinają przekątną
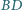 odpowiednio w punktach
odpowiednio w punktach
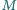 i
i
 Udowodnij, że punkty
Udowodnij, że punkty
 leżą na
jednym okręgu.
leżą na
jednym okręgu.
 będzie punktem styczności prostej
będzie punktem styczności prostej
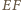 do danego
okręgu. Wtedy
do danego
okręgu. Wtedy
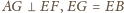 oraz
oraz
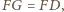 zatem
zatem
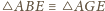 oraz
oraz
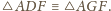 Stąd
Stąd
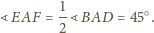
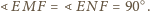
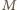 i
i
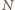 leżą na okręgu o średnicy
leżą na okręgu o średnicy
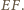 Leży na nim też punkt
Leży na nim też punkt
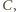 bo
bo
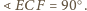
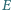 i
i
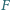 leżą odpowiednio na bokach
leżą odpowiednio na bokach
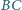 i
i
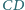 kwadratu
kwadratu
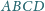 o boku 1, przy czym
o boku 1, przy czym
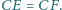 Punkt
Punkt
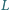 to rzut punktu
to rzut punktu
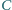 na prostą
na prostą
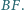 Wykaż, że
Wykaż, że
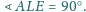
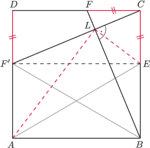
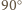 wokół środka. Obrazem punktu
wokół środka. Obrazem punktu
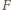 jest
taki punkt
jest
taki punkt
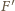 na boku
na boku
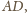 że
że
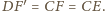 Obrazem
prostej
Obrazem
prostej
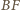 jest prosta
jest prosta
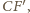 jest ona prostopadła do
jest ona prostopadła do
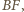 więc
zawiera punkt
więc
zawiera punkt
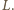 Opiszmy okrąg na prostokącie
Opiszmy okrąg na prostokącie
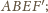 jego
średnicą jest
jego
średnicą jest
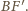 Punkt
Punkt
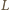 leży na tym okręgu, ponieważ kąt
leży na tym okręgu, ponieważ kąt
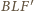 jest prosty. Średnicą okręgu jest także
jest prosty. Średnicą okręgu jest także
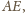 więc również
kąt
więc również
kąt
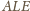 jest prosty.
jest prosty.
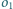 i
i
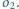 Znajdź inwersję przekształcającą
Znajdź inwersję przekształcającą
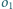 na
na
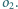
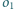 i
i
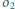 będą rozłącznymi okręgami, takimi że
będą rozłącznymi okręgami, takimi że
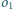 leży we wnętrzu
leży we wnętrzu
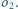 Rysujemy okrąg
Rysujemy okrąg
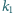 styczny
zewnętrznie do
styczny
zewnętrznie do
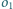 i wewnętrznie do
i wewnętrznie do
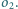 Następnie rysujemy okrąg
Następnie rysujemy okrąg
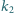 styczny zewnętrznie do
styczny zewnętrznie do
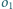 i
i
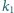 oraz wewnętrznie do
oraz wewnętrznie do
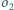 itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
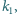 to mówimy, że okręgi
to mówimy, że okręgi
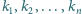 tworzą
łańcuch Steinera okręgów
tworzą
łańcuch Steinera okręgów
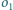 i
i
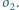 Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
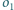 i
i
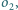 to jest to niezależne od
położenia pierwszego okręgu
to jest to niezależne od
położenia pierwszego okręgu
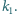
 i dwa rozłączne okręgi
i dwa rozłączne okręgi
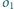 i
i
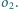 Narysuj
okrąg styczny do
Narysuj
okrąg styczny do
 i prostopadły do okręgów
i prostopadły do okręgów
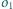 i
i
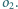
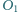 i skali
i skali
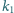 z jednokładnością o środku
z jednokładnością o środku
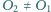 i skali
i skali
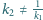 jest
jednokładnością o środku na prostej
jest
jednokładnością o środku na prostej
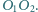
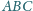 obrano punkt
obrano punkt
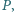 taki że
taki że
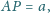

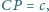 gdzie
gdzie
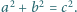 Wyznaczyć długość boku trójkąta
Wyznaczyć długość boku trójkąta
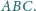
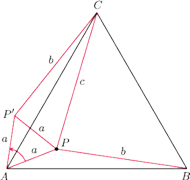
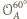 oraz punkt
oraz punkt
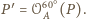 Zauważmy, że
Zauważmy, że
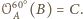 Tak więc
Tak więc
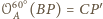 i w szczególności
i w szczególności
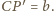 Trójkąt
Trójkąt
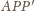 jest równoboczny, więc
jest równoboczny, więc
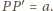 Z założeń wynika, iż
Z założeń wynika, iż
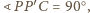 czyli
czyli
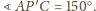 Stosując twierdzenie kosinusów
do trójkąta
Stosując twierdzenie kosinusów
do trójkąta
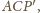 uzyskujemy
uzyskujemy
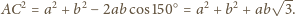
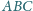 i
i
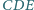 (mające wspólny wierzchołek
(mające wspólny wierzchołek
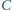 ) oraz punkty
) oraz punkty
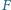 i
i
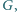 takie
że
takie
że
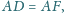
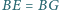 i
i
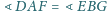 (jako kąty
skierowane). Wykazać, że trójkąt
(jako kąty
skierowane). Wykazać, że trójkąt
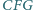 jest równoboczny.
jest równoboczny.
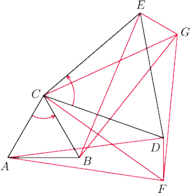
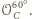 Zauważmy, że
Zauważmy, że
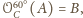
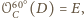 czyli
czyli
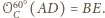 Stąd w szczególności
Stąd w szczególności
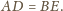 Na podstawie założeń (
Na podstawie założeń (
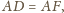
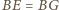 oraz
oraz
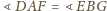 ) trójkąty
) trójkąty
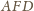 i
i
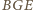 są przystające.
Tak więc
są przystające.
Tak więc
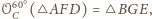 czyli
czyli
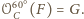
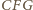 jest zatem równoboczny.
jest zatem równoboczny.
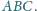 Rozważamy wszystkie takie
trójkąty równoboczne
Rozważamy wszystkie takie
trójkąty równoboczne
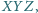 że punkty
że punkty
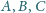 są punktami
wewnętrznymi odcinków
są punktami
wewnętrznymi odcinków
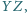
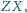
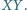 Dowieść, że
środki ciężkości wszystkich rozważanych trójkątów leżą na jednym
okręgu.
Dowieść, że
środki ciężkości wszystkich rozważanych trójkątów leżą na jednym
okręgu.
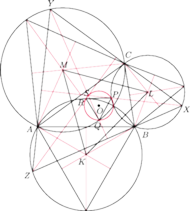
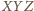 spełniający warunki zadania. Niech
spełniający warunki zadania. Niech
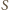 będzie jego środkiem ciężkości. Zauważmy, że bok
będzie jego środkiem ciężkości. Zauważmy, że bok
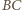 jest
widziany z punktu
jest
widziany z punktu
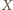 pod kątem
pod kątem
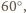 a więc
a więc
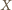 leży
na okręgu opisanym na trójkącie równobocznym zbudowanym zewnętrznie
na boku
leży
na okręgu opisanym na trójkącie równobocznym zbudowanym zewnętrznie
na boku
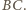 Analogicznie
Analogicznie
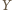 i
i
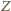 leżą na okręgach
opisanych na trójkątach równobocznych zbudowanych odpowiednio
na bokach
leżą na okręgach
opisanych na trójkątach równobocznych zbudowanych odpowiednio
na bokach
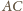 i
i
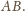
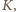
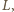
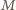 kolejne środki tych okręgów.
Z twierdzenia Napoleona (patrz np. Delta 6/2004) wynika, że trójkąt
kolejne środki tych okręgów.
Z twierdzenia Napoleona (patrz np. Delta 6/2004) wynika, że trójkąt
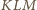 jest równoboczny. Niech
jest równoboczny. Niech
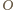 oznacza jego środek
ciężkości. Proste
oznacza jego środek
ciężkości. Proste
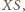
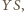
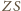 (jako dwusieczne kątów
wewnętrzych trójkąta
(jako dwusieczne kątów
wewnętrzych trójkąta
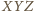 ) przecinają w połowie krótsze łuki
) przecinają w połowie krótsze łuki
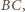
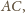
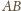 narysowanych okręgów. Środki tych
łuków oznaczmy kolejno przez
narysowanych okręgów. Środki tych
łuków oznaczmy kolejno przez
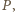
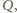
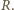 Zauważmy,
że
Zauważmy,
że
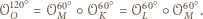
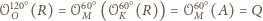
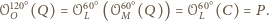
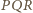 jest równoboczny
i jego środkiem ciężkości jest punkt
jest równoboczny
i jego środkiem ciężkości jest punkt
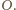 Pozostaje wykazać, iż
Pozostaje wykazać, iż
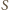 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie
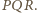 W tym celu,
ponieważ
W tym celu,
ponieważ
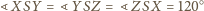
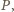
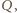
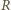 należą odpowiednio do prostych
należą odpowiednio do prostych
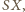
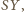
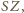 wystarczy zauważyć, że
wystarczy zauważyć, że
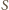 nie jest punktem
wewnętrznym trójkąta
nie jest punktem
wewnętrznym trójkąta
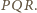 W przeciwnym razie, boki trójkąta
W przeciwnym razie, boki trójkąta
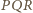 są widziane z punktu
są widziane z punktu
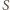 pod kątem
pod kątem
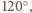 a więc
a więc
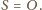 Wtedy punkt
Wtedy punkt
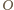 leży na zewnątrz okręgów opisanych
na „dobudowanych” na początku trójkątach równobocznych. Oznacza to, że
każdy z kątów
leży na zewnątrz okręgów opisanych
na „dobudowanych” na początku trójkątach równobocznych. Oznacza to, że
każdy z kątów
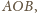
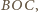
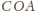 ma miarę mniejszą od
ma miarę mniejszą od
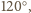 co jest niemożliwe.
co jest niemożliwe.
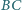 i
i
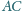 trójkąta
trójkąta
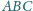 są jednocześnie bokami
kwadratów
są jednocześnie bokami
kwadratów
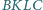 i
i
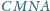 (leżących na zewnątrz trójkąta
(leżących na zewnątrz trójkąta
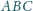 ). Punkty
). Punkty
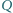 i
i
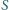 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
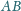 i
i
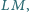 a
a
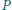 i
i
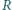 środkami kwadratów
środkami kwadratów
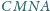 i
i
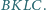 Wykazać, że czworokąt
Wykazać, że czworokąt
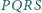 jest
kwadratem.
jest
kwadratem.
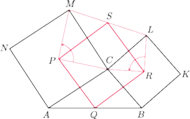
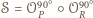 będące złożeniem dwóch
obrotów o kąt
będące złożeniem dwóch
obrotów o kąt
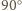 wokół punktów
wokół punktów
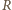 i
i
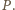 Na podstawie
Na podstawie
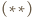
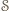 jest symetrią środkową względem punktu
jest symetrią środkową względem punktu
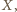 takiego
że
takiego
że
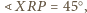
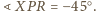 Z drugiej strony zauważmy,
że
Z drugiej strony zauważmy,
że
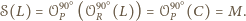
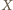 symetrii
symetrii
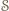 pokrywa się ze środkiem
pokrywa się ze środkiem
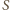 odcinka
odcinka
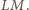 W szczególności
W szczególności
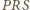 jest równoramiennym
trójkątem prostokątnym. Rozważając analogicznie złożenie obrotów
jest równoramiennym
trójkątem prostokątnym. Rozważając analogicznie złożenie obrotów
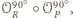 dowodzimy, że
dowodzimy, że
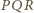 jest również równoramiennym
trójkątem prostokątnym. Tak więc czworokąt
jest również równoramiennym
trójkątem prostokątnym. Tak więc czworokąt
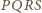 jest kwadratem.
jest kwadratem.