Delta mi!

Za co Hillel Furstenberg (Uniwersytet Hebrajski w Jerozolimie) oraz Gregory Margulis (Uniwersytet Yale w New Haven) otrzymali tegoroczną nagrodę?

Człowiek to istota nie tylko myśląca, ale i mierząca - można by rzec górnolotnie, że mierzenie (rozmiarów wrogiej armii, zaopatrzenia spichrzów, stanu skarbca itp.) leży u podstaw naszej cywilizacji. W języku matematyki miara jest definiowana przez następujące, zdroworozsądkowe warunki...

Chociaż są to pojęcia abstrakcyjne (bo przecież nikt nie widział ani punktu, ani odcinka), przemawiają dobrze do wyobraźni i zgadzają się ze zdrowym rozsądkiem. I aż dziw bierze, jak wiele wokół nas zjawisk, które zdają się ostrzegać: uwaga to co wydaje się takie oczywiste, wcale nie musi być prawdziwe.

W 1641 roku ukazały się Centrobaryca Paula Guldina, a w nich twierdzenie znane dziś jako reguły Guldina...

Wymienione w tytule tematy uchodzą za trudne. Tym ważniejsze jest zacząć od rzeczy prostych i powszechnie znanych...

Wyobraźmy sobie następującą grę. Mamy planszę o polach ponumerowanych od 0 do 100 i dwa pionki, stojące na początku na polu o numerze 0. Gracze wykonują ruchy na przemian. Gracz rzuca monetą i jeśli wypadnie reszka, to przesuwa swój pionek o 1 pole, a jeśli orzeł – o 5 pól. Wygrywa ten, kto pierwszy dojdzie do pola o numerze 100.

Zasada Cavalieriego dla figur płaskich brzmi:
jeżeli dwie figury płaskie w przecięciu z każdą prostą równoległą do danej dają przekrój o tej samej długości, to pola tych figur są równe.

Tangram to stara chińska zabawa, polegająca na układaniu zadanych figur z siedmiu klocków, ułożonych na rysunku 1 w kwadrat.

W numerze poświęconym mierze (8/2008) nie sposób pominąć tych pierwszych, czyli zwykłych miar geometrycznych (zważmy, że geometria ma miarę w swojej nazwie).Wydaje się, że wiemy o nich wszystko, bo przecież stykaliśmy się z nimi niemal od zerówki. Okazuje się jednak, że i na ich temat można postawić pytania o nieoczywistych odpowiedziach.

Korzenie teorii miary sięgają tak podstawowych pojęć, jak długość (np. odcinka), pole (np. koła) i objętość (np. kuli). Wraz z rozwojem matematyki konieczne stało się uogólnienie tych pojęć w taki sposób, żeby dało się „zmierzyć” coraz bardziej skomplikowane podzbiory danej przestrzeni – na przykład prostej rzeczywistej 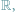do której w tym artykule ograniczymy nasze rozważania.

Jak wiadomo, komputery traktują wszystkie dane, na których działają, jako ciągi bitów, z których każdy może mieć dwie wartości (0 lub 1). Przykładowo, ten tekst jest zapisany w ten sposób, że każdej z liter i pozostałych znaków odpowiada ciąg 8 bitów. Daje to 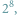czyli 256 możliwości, co w zupełności wystarcza do zapisania wszystkich potrzebnych znaków. Jednak w rzeczywistości różnych znaków występujących w tekście jest mniej. Problem jest więc taki: jak zapisać tekst tak, żeby na każdą jego literę przypadało jak najmniej bitów?

Czy zastanawiałeś się, drogi Czytelniku, dlaczego wyszukiwarka wyświetla adresy stron będących odpowiedzią na Twoje zapytanie właśnie w takiej, a nie innej kolejności?

Czy przyszło Wam kiedyś do głowy, drodzy Czytelnicy, mierzyć nitką objętość? Albo pole?