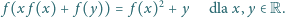Niech
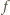 będzie funkcją, spełniającą podane równania. Wykażemy,
że jest to funkcja nieparzysta. Z drugiego równania widać, że
będzie funkcją, spełniającą podane równania. Wykażemy,
że jest to funkcja nieparzysta. Z drugiego równania widać, że
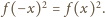 Tak więc
Tak więc
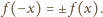 Przypuśćmy, że dla
pewnej liczby
Przypuśćmy, że dla
pewnej liczby
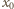 zachodzi równość
zachodzi równość
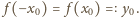 Wystarczy
pokazać, że
Wystarczy
pokazać, że
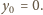 Otóż
Otóż
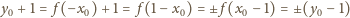
(ostatnia równość wynika ze spostrzeżenia, że
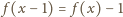 dla
wszystkich
dla
wszystkich
 ). Stąd
). Stąd
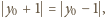 co jest prawdą jedynie dla
co jest prawdą jedynie dla
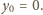 Zatem
Zatem
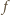 jest funkcją nieparzystą.
jest funkcją nieparzystą.
Dla
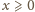 mamy
mamy
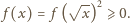 Wobec nieparzystości,
Wobec nieparzystości,
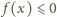 dla
dla
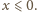 Dla
Dla
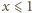 dostajemy oszacowanie
dostajemy oszacowanie
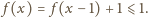 To znaczy, że funkcja
To znaczy, że funkcja
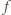 odwzorowuje
przedział
odwzorowuje
przedział
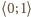 w siebie. Z równania
w siebie. Z równania
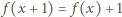 wynika
teraz, że funkcja
wynika
teraz, że funkcja
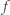 odwzorowuje każdy przedział postaci
odwzorowuje każdy przedział postaci
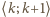 w siebie
w siebie
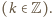 Zachodzi więc nierówność
Zachodzi więc nierówność
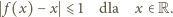
Weźmy dowolną liczbę
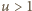 i oznaczmy
i oznaczmy
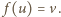 Z równania
Z równania
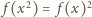 dostajemy
dostajemy
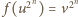 dla
dla
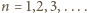 Stąd
Stąd
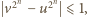 czyli
czyli
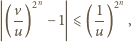
co w granicy (przy
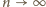 ) daje równość
) daje równość
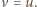 Wykazaliśmy
w ten sposób, że
Wykazaliśmy
w ten sposób, że
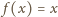 dla
dla
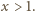
Dzięki równości
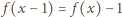 wnosimy stąd, że
wnosimy stąd, że
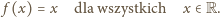
Funkcja identycznościowa spełnia oba równania układu i jest jego jedynym
rozwiązaniem.
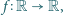 które spełniają układ równań
funkcyjnych
które spełniają układ równań
funkcyjnych
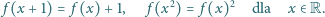
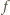 będzie funkcją, spełniającą podane równania. Wykażemy,
że jest to funkcja nieparzysta. Z drugiego równania widać, że
będzie funkcją, spełniającą podane równania. Wykażemy,
że jest to funkcja nieparzysta. Z drugiego równania widać, że
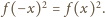 Tak więc
Tak więc
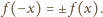 Przypuśćmy, że dla
pewnej liczby
Przypuśćmy, że dla
pewnej liczby
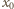 zachodzi równość
zachodzi równość
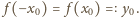 Wystarczy
pokazać, że
Wystarczy
pokazać, że
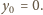 Otóż
Otóż
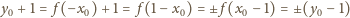
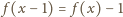 dla
wszystkich
dla
wszystkich
 ). Stąd
). Stąd
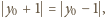 co jest prawdą jedynie dla
co jest prawdą jedynie dla
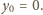 Zatem
Zatem
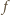 jest funkcją nieparzystą.
jest funkcją nieparzystą.
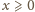 mamy
mamy
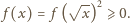 Wobec nieparzystości,
Wobec nieparzystości,
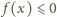 dla
dla
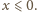 Dla
Dla
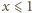 dostajemy oszacowanie
dostajemy oszacowanie
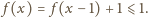 To znaczy, że funkcja
To znaczy, że funkcja
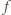 odwzorowuje
przedział
odwzorowuje
przedział
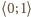 w siebie. Z równania
w siebie. Z równania
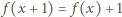 wynika
teraz, że funkcja
wynika
teraz, że funkcja
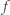 odwzorowuje każdy przedział postaci
odwzorowuje każdy przedział postaci
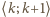 w siebie
w siebie
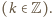 Zachodzi więc nierówność
Zachodzi więc nierówność
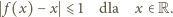
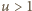 i oznaczmy
i oznaczmy
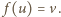 Z równania
Z równania
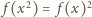 dostajemy
dostajemy
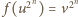 dla
dla
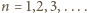 Stąd
Stąd
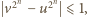 czyli
czyli
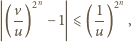
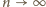 ) daje równość
) daje równość
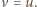 Wykazaliśmy
w ten sposób, że
Wykazaliśmy
w ten sposób, że
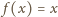 dla
dla
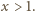
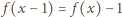 wnosimy stąd, że
wnosimy stąd, że
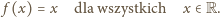
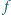 postaci
postaci
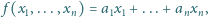
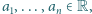 które na zbiorze
które na zbiorze
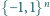 przyjmują
tylko dwie wartości:
przyjmują
tylko dwie wartości:
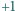 lub
lub
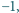 tzn. takie, że jeśli
tzn. takie, że jeśli
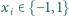 dla
dla
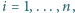 to
to
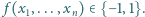
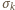 operację polegającą na zmianie znaku na
operację polegającą na zmianie znaku na
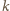 -tej
współrzędnej
-tej
współrzędnej
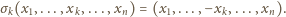
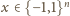 zachodzi równość
zachodzi równość
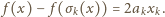
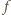 przyjmuje tylko wartości 1 i
przyjmuje tylko wartości 1 i
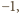 to ta
różnica może przyjmować tylko trzy wartości:
to ta
różnica może przyjmować tylko trzy wartości:
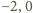 i
i
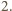 Zatem dla tych
Zatem dla tych
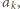 które są niezerowe, musi być
które są niezerowe, musi być
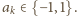
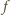 ma dokładnie jeden niezerowy
współczynnik. Załóżmy przeciwnie, że ma przynajmniej dwa, np.
ma dokładnie jeden niezerowy
współczynnik. Załóżmy przeciwnie, że ma przynajmniej dwa, np.
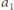 i
i
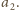 Bez utraty ogólności możemy przyjąć, że
Bez utraty ogólności możemy przyjąć, że
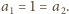 Wówczas, oznaczając przez
Wówczas, oznaczając przez
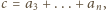 mamy
mamy
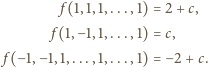
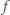 przyjmuje w tych trzech punktach trzy różne
wartości, co przeczy temu, że wartości
przyjmuje w tych trzech punktach trzy różne
wartości, co przeczy temu, że wartości
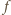 należą do zbioru
dwuelementowego. Zatem
należą do zbioru
dwuelementowego. Zatem
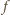 jest postaci
jest postaci
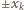 dla pewnego
dla pewnego
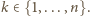
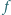 zadany wzorem
zadany wzorem
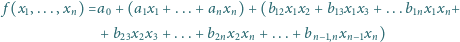
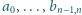 są
niezerowe, i o tej własności, że na zbiorze
są
niezerowe, i o tej własności, że na zbiorze
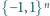 przyjmuje on tylko
wartości
przyjmuje on tylko
wartości
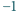 i
i
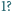 A jeśli założymy, że dokładnie cztery
współczynniki mają być niezerowe?
A jeśli założymy, że dokładnie cztery
współczynniki mają być niezerowe?
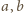 i
i
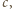 stojące zaś
przy nich jednomiany nazwijmy odpowiednio
stojące zaś
przy nich jednomiany nazwijmy odpowiednio
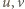 i
i
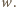 Załóżmy,
że wśród tych jednomianów najwyższy stopień ma
Załóżmy,
że wśród tych jednomianów najwyższy stopień ma
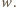 Istnieje
wtedy zmienna, która występuje w
Istnieje
wtedy zmienna, która występuje w
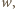 ale nie występuje w
ale nie występuje w
 lub
lub
 – bez utraty ogólności możemy przyjąć, że
– bez utraty ogólności możemy przyjąć, że
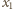 ma tę
własność. Wówczas
ma tę
własność. Wówczas
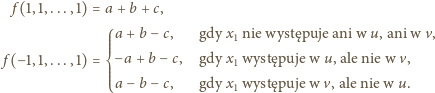
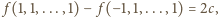 ale
z drugiej strony, skoro
ale
z drugiej strony, skoro
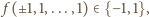 to
to
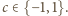 Z zadania
1394 wiemy, że
Z zadania
1394 wiemy, że
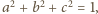 otrzymujemy więc
otrzymujemy więc
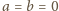 wbrew
założeniu. Pozostałe przypadki wymagają analogicznego rozumowania.
wbrew
założeniu. Pozostałe przypadki wymagają analogicznego rozumowania.
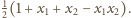
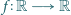 będzie ograniczona z góry, tzn. istnieje taka
liczba
będzie ograniczona z góry, tzn. istnieje taka
liczba
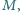 że
że
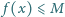 dla każdego
dla każdego
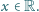 Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
Udowodnić,
że jeśli dla wszystkich liczb rzeczywistych
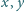 spełniona jest
nierówność
spełniona jest
nierówność
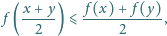
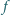 jest funkcją stałą.
jest funkcją stałą.
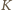 będzie najmniejszą liczbą o tej własności, że
będzie najmniejszą liczbą o tej własności, że
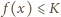 dla
każdej liczby rzeczywistej
dla
każdej liczby rzeczywistej
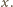 Pokażemy, że wówczas
Pokażemy, że wówczas
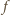 jest
funkcją stałą, równą
jest
funkcją stałą, równą
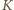 w każdym punkcie. Załóżmy nie wprost, że
dla pewnego
w każdym punkcie. Załóżmy nie wprost, że
dla pewnego
 jest
jest
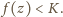 Skoro
Skoro
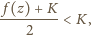
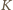 znajdziemy liczbę
znajdziemy liczbę
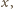 dla której
dla której
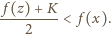
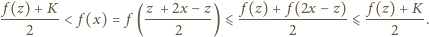
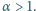 Obliczyć minimalną wartość
funkcji
Obliczyć minimalną wartość
funkcji
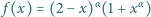
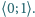
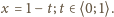 Uzyskujemy ciąg
zależności (korzystając w pewnym momencie z nierówności Bernoulliego
dla wykładnika rzeczywistego
Uzyskujemy ciąg
zależności (korzystając w pewnym momencie z nierówności Bernoulliego
dla wykładnika rzeczywistego
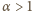 ):
):
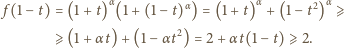
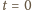 nierówność staje się równością:
nierówność staje się równością:
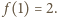 Jest to
wartość minimalna funkcji
Jest to
wartość minimalna funkcji
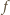 na przedziale
na przedziale
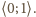
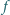 przekształcająca zbiór liczb
dodatnich w siebie, spełniająca dla wszystkich dodatnich
przekształcająca zbiór liczb
dodatnich w siebie, spełniająca dla wszystkich dodatnich
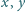 nierówność
nierówność
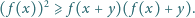
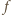 istnieje. Zauważmy, że
istnieje. Zauważmy, że
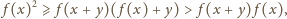
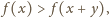 dla dowolnych
dla dowolnych
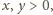 co oznacza, że
co oznacza, że
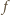 jest malejąca. Warunek z treści zadania można zapisać tak:
jest malejąca. Warunek z treści zadania można zapisać tak:
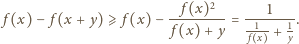
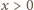 i weźmy taką liczbę całkowitą
i weźmy taką liczbę całkowitą
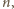 aby
aby
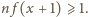 Wtedy dla
Wtedy dla
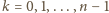 mamy
mamy
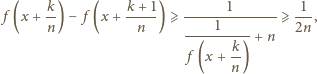
 nierówności, dostajemy
nierówności, dostajemy
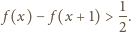
 zachodzi
nierówność
zachodzi
nierówność
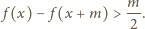
 tak duże, aby było
tak duże, aby było
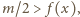 otrzymujemy
otrzymujemy
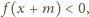 co przeczy temu, że
co przeczy temu, że
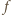 przyjmuje wyłącznie
wartości dodatnie.
przyjmuje wyłącznie
wartości dodatnie.
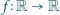 będzie funkcją ściśle rosnącą, odwzorowującą zbiór
wszystkich liczb wymiernych
będzie funkcją ściśle rosnącą, odwzorowującą zbiór
wszystkich liczb wymiernych
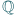 na cały zbiór
na cały zbiór
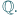 Czy stąd wynika,
że funkcja
Czy stąd wynika,
że funkcja
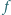 jest przedziałami liniowa (tzn. że
jest przedziałami liniowa (tzn. że
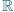 jest sumą
skończenie lub nieskończenie wielu przedziałów dodatniej długości,
o rozłącznych wnętrzach, i w każdym z tych przedziałów
jest sumą
skończenie lub nieskończenie wielu przedziałów dodatniej długości,
o rozłącznych wnętrzach, i w każdym z tych przedziałów
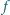 jest
liniowa)?
jest
liniowa)?
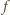 najpierw
w przedziale
najpierw
w przedziale
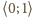 wzorem
wzorem
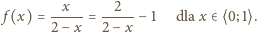
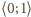 na cały ten przedział; łatwo wyznaczyć funkcję
odwrotną:
na cały ten przedział; łatwo wyznaczyć funkcję
odwrotną:
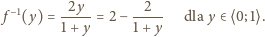
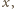
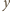 są liczbami wymiernymi z przedziału
są liczbami wymiernymi z przedziału
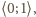 to
to
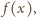
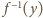 też są liczbami wymiernymi
z przedziału
też są liczbami wymiernymi
z przedziału
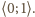 Zatem obrazem zbioru
Zatem obrazem zbioru
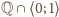 jest
ten sam zbiór.
jest
ten sam zbiór.
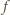 do funkcji
do funkcji
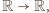 przesuwając jej wykres
o wektor
przesuwając jej wykres
o wektor
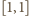 i jego całkowite wielokrotności. Formalnie: przyjmujemy
i jego całkowite wielokrotności. Formalnie: przyjmujemy

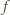 jest ściśle rosnąca; w każdym
z przedziałów
jest ściśle rosnąca; w każdym
z przedziałów
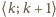 jest ściśle wypukła – więc nie jest liniowa
w żadnym przedziale długości dodatniej. Wreszcie, jest jasne, że obrazem
zbioru
jest ściśle wypukła – więc nie jest liniowa
w żadnym przedziale długości dodatniej. Wreszcie, jest jasne, że obrazem
zbioru
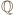 jest cały zbiór
jest cały zbiór
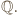
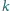 będzie liczbą naturalną większą od 1. Dla jakich dodatnich liczb
rzeczywistych
będzie liczbą naturalną większą od 1. Dla jakich dodatnich liczb
rzeczywistych
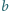 można znaleźć funkcję
można znaleźć funkcję
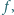 ciągłą na przedziale
ciągłą na przedziale
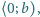 różniczkowalną wewnątrz tego przedziału oraz spełniającą
warunki:
różniczkowalną wewnątrz tego przedziału oraz spełniającą
warunki:
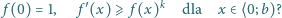
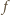 będzie funkcją, spełniającą podane warunki. Zauważmy, że
będzie funkcją, spełniającą podane warunki. Zauważmy, że
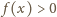 w przedziale
w przedziale
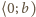 (w przeciwnym razie, oznaczając przez
(w przeciwnym razie, oznaczając przez
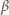 najmniejsze miejsce zerowe funkcji
najmniejsze miejsce zerowe funkcji
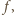 mielibyśmy w przedziale
mielibyśmy w przedziale
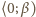 nierówności
nierówności
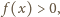
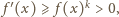 skąd
skąd
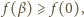 czyli
czyli
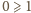 ).
).
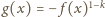 z pochodną
z pochodną
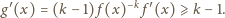
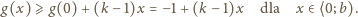
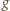 w przedziale
w przedziale
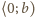 są ujemne. Tak więc
są ujemne. Tak więc
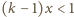 dla wszystkich
dla wszystkich
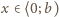 ; to znaczy, że liczba
; to znaczy, że liczba
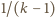 nie należy do tego przedziału – czyli zachodzi nierówność
nie należy do tego przedziału – czyli zachodzi nierówność
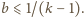 Na odwrót, jeżeli
Na odwrót, jeżeli
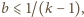 to określamy
funkcję
to określamy
funkcję
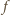 wzorem
wzorem
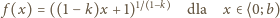
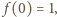
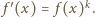 Stąd
odpowiedź: liczby
Stąd
odpowiedź: liczby
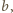 o które pyta zadanie, są scharakteryzowane
nierównością
o które pyta zadanie, są scharakteryzowane
nierównością
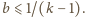
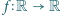 jest dana wzorem
jest dana wzorem
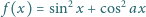
 ). Dowieść, że jeżeli
). Dowieść, że jeżeli
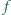 jest
funkcją okresową, to
jest
funkcją okresową, to
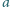 jest liczbą wymierną.
jest liczbą wymierną.
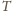 będzie okresem funkcji
będzie okresem funkcji
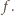 Z równości
Z równości
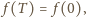 czyli
czyli
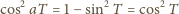
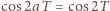 ) wnosimy, że
) wnosimy, że
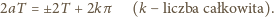
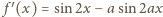 też jest funkcją
też jest funkcją
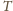 -okresową:
-okresową:
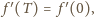 czyli
czyli
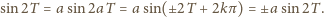
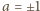 (liczba wymierna), albo
(liczba wymierna), albo
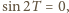 skąd
skąd
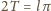 (
(
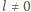 ),
),
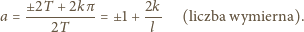
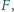 określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
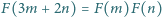 dla każdej pary liczb
całkowitych
dla każdej pary liczb
całkowitych
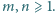
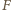 będzie jedną z szukanych funkcji. Oznaczmy wartości
będzie jedną z szukanych funkcji. Oznaczmy wartości
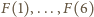 kolejno przez
kolejno przez
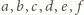 ; oznaczmy ponadto
; oznaczmy ponadto
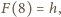
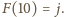 Kładąc w równaniu
Kładąc w równaniu
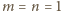 oraz
oraz
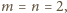 dostajemy
dostajemy

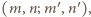 w której
w której
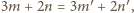 daje
informację w postaci równości
daje
informację w postaci równości
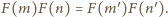 Biorąc czwórki
Biorąc czwórki
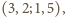
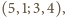
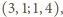
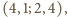
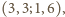 otrzymujemy
w ten sposób związki
otrzymujemy
w ten sposób związki
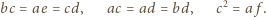
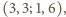
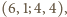
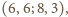
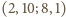 dają
zależności
dają
zależności
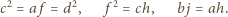
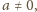 to z pierwszej równości (1) oraz ze związków (2)
wnosimy kolejno, że
to z pierwszej równości (1) oraz ze związków (2)
wnosimy kolejno, że
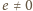 ;
;
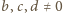 ;
;
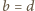 ;
;
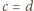 ;
;
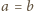 ;
;
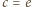 ;
;
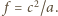 Tak więc
Tak więc
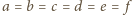 ;
skoro zaś
;
skoro zaś
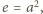 ta wspólna wartość wynosi 1.
ta wspólna wartość wynosi 1.
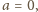 to korzystamy z zależności (3) oraz (1) i łatwo
stwierdzamy, że
to korzystamy z zależności (3) oraz (1) i łatwo
stwierdzamy, że
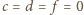 ;
;
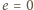 ;
;
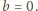 Zatem na
zbiorze
Zatem na
zbiorze
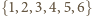 funkcja
funkcja
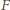 jest stała, o wartości
1 lub 0. Każda liczba naturalna
jest stała, o wartości
1 lub 0. Każda liczba naturalna
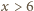 daje się zapisać w postaci
daje się zapisać w postaci
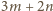 dla pewnych
dla pewnych
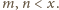 Przez oczywistą indukcję
uzyskujemy wniosek, że
Przez oczywistą indukcję
uzyskujemy wniosek, że
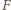 jest funkcją tożsamościowo równą
1 lub 0. Każda z nich spełnia zadane równanie.
jest funkcją tożsamościowo równą
1 lub 0. Każda z nich spełnia zadane równanie.
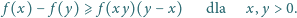
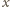 i
i
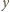 , a następnie mnożąc uzyskaną
nierówność przez
, a następnie mnożąc uzyskaną
nierówność przez
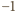 , otrzymujemy nierówność taką samą, jak
wyjściowa, lecz przeciwnie skierowaną. Treścią zadania jest więc równanie
funkcyjne
, otrzymujemy nierówność taką samą, jak
wyjściowa, lecz przeciwnie skierowaną. Treścią zadania jest więc równanie
funkcyjne
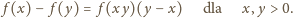
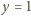 i oznaczając
i oznaczając
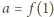 , dostajemy równanie
, dostajemy równanie
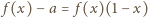 , czyli
, czyli
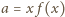 . Zatem
. Zatem

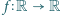 , spełniające równanie
, spełniające równanie