Piszemy tutaj "nieskończoności", mając oczywiście na myśli możliwe liczności, czyli moce, nieskończonych zbiorów. Matematycy nazywają je też liczbami kardynalnymi. Będziemy mówić, że jedna "nieskończoność" (liczność lub moc zbioru 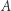) jest mniejsza od drugiej "nieskończoności" (liczności lub mocy zbioru 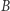), jeśli wszystkich elementów zbioru 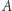nie da się ustawić w pary ze wszystkimi elementami zbioru 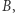ale można je ustawić z pewną częścią zbioru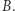

W poprzednich odcinkach rozmawialiśmy o twierdzeniu Cantora. Mówi ono, że każdy zbiór 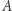ma tę cechę, że zbiór 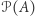wszystkich podzbiorów zbioru 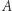nie jest równoliczny ze zbiorem 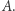Skoro jednak dla każdego elementu zbioru 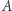do zbioru 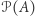należy 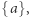czyli jednoelementowy podzbiór z tym elementem, to część zbioru 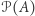złożona z jednoelementowych zbiorów jest równoliczna ze zbiorem 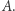Możemy zatem powiedzieć, że moc zbioru 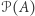jest większa od mocy zbioru 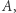co oznaczamy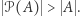

Znając to twierdzenie, bez trudu możemy tworzyć coraz większe nieskończoności. Rzeczywiście, niech 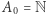to zbiór liczb naturalnych. Wtedy niech 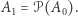Oczywiście, 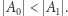Niech zatem 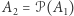i w takim razie 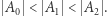I tak dalej, niech 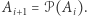Otrzymujemy w ten sposób

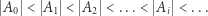nieskończony ciąg coraz większych nieskończoności!

Ale i ten nieskończony ciąg nieskończoności to jeszcze nie koniec. Niech bowiem

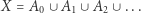będzie sumą wszystkich tych nieskończenie wielu zbiorów. Zauważmy, że 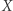jest jeszcze większy niż którykolwiek z nich. Rzeczywiście, dla dowolnego 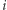mamy 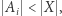bowiem zbiór 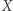zawiera zbiór 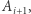a przecież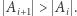

I to także oczywiście nie koniec, bo przecież możemy wziąć zbiór wszystkich podzbiorów tak zdefiniowanego zbioru 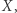aby otrzymać zbiór o jeszcze większej liczności. I tak dalej. W pewnym sensie w nieskończoność i za nieskończonością w nieskończoność.

Ale i na tym nie kończy się nasza przygoda. Przyjrzyjmy się temu procesowi tworzenia coraz większych "nieskończoności" bardziej metodycznie. Metodę tworzenia z liczności 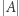większej liczności 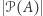będziemy tu nazywać metodą podzbiorów. Metodą sumy będziemy nazywać stworzenie z nieskończonej rodziny zbiorów, w której dla każdego zbioru 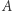z tej rodziny jest w tej rodzinie zbiór 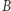taki, że 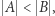zbioru jeszcze większego od dowolnego jej elementu, mianowicie jej sumy.

Zauważmy jednak, że metodą podzbiorów niekoniecznie z danej liczności otrzymamy najmniejszą liczność większą od niej. Być może istnieją liczby kardynalne pomiędzy 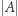oraz 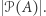Zresztą właśnie hipoteza continuum odnosi się do tego typu rozważań.

Okazuje się, na szczęście (choć aby podać dowód tego faktu, potrzebne są definicje, które wykraczają poza tę serię artykułów), że dla każdej rodziny "nieskończoności" istnieje w niej "nieskończoność" najmniejsza. W szczególności, wynika z tego, że dla danego zbioru 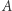można znaleźć pewien zbiór 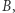o liczności najmniejszej z tych, które są większe od liczności zbioru 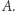To przejście będziemy nazywać metodą następnikową.

Z reguły kolejne możliwe nieskończone liczby kardynalne oznacza się za pomocą pierwszej litery z języka hebrajskiego 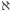(alef) z odpowiednim indeksem. Tak więc 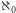to liczność zbioru liczb naturalnych, a 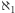to najmniejsza liczba kardynalna większa od 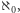zaś 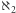to najmniejsza liczba kardynalna większa od 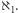Hipotezę continuum możemy więc sformułować jako stwierdzenie, że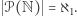

Warto w tym momencie odnotować wprost dwa mniej lub bardziej zaskakujące wnioski. Po pierwsze, nie istnieje największa "nieskończoność". Rzeczywiście, dla każdego zbioru 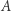istnieje zbiór o większej mocy, mianowicie zbiór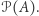

Drugi wniosek jest następujący: nie istnieje zbiór wszystkich "nieskończoności". Znów, załóżmy przeciwnie, że taki zbiór istnieje. Ale zgodnie z poprzednim wnioskiem, skoro nie ma największej liczby kardynalnej, to dla każdej liczby kardynalnej w tym zbiorze jest w nim też większa liczba kardynalna. Ale w takim razie możemy metodą sumowania (biorąc sumę wszystkich elementów tego zbioru) wyprodukować jeszcze większą liczbę kardynalną, która jest większa od każdej z tego zbioru, więc nie jest elementem tego zbioru. Ale zbiór miał zawierać wszystkie liczby kardynalne, co stanowi sprzeczność.

Niemniej znaleźliśmy trzy metody konstruowania coraz większych liczb kardynalnych: metodę następnikową, metodę podzbiorów i metodę sumowania. Nasuwa się od razu nurtujące pytanie. Czy poczynając od liczności zbioru liczb naturalnych, można "dojść" do dowolnej "nieskończoności" (liczby kardynalnej), stosując te trzy metody?

Potrzebne będą nam jeszcze dwie definicje. Powiemy, że pewna liczba kardynalna jest graniczna, jeśli wśród mniejszych od niej nie ma największej. Zauważmy, że 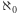jest graniczną liczbą kardynalną, bowiem każdy zbiór o liczności mniejszej niż jego moc to zbiór skończony. A zatem liczności mniejsze od 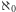to po prostu skończone liczby i nie ma wśród nich największej.

Druga definicja to regularność "nieskończoności". Powiemy, że pewna liczba kardynalna jest regularna, jeśli nie da się jej otrzymać metodą sumy ze zbioru liczności mniejszych od niej, który sam ma od niej mniejszą liczność. Ponownie zauważmy, że 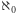jest liczbą regularną, bowiem skończona suma skończonych zbiorów jest tylko skończona. Niemniej nie każda "nieskończoność" jest regularna. Na przykład zastosujmy metodę sumy do zbioru liczb kardynalnych 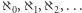Skoro elementy tego zbioru w oczywisty sposób są ponumerowane liczbami naturalnymi, to jest ich tyle samo co liczb naturalnych, czyli 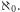Jednak liczba, którą dostaniemy, jest większa od każdej z nich, i w szczególności od 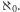Nie jest więc regularna.

Inaczej mówiąc, liczb kardynalnych granicznych nie można skonstruować metodą następnikową z mniejszych liczności. Za to liczb kardynalnych regularnych nie da się skonstruować metodą sumowania, używając tylko zbiorów o mniejszej mocy. Matematycy nazywają liczbę kardynalną większą od liczności zbioru liczb naturalnych słabo nieosiągalną, jeśli łączy w sobie te dwie cechy, czyli jeśli jest regularna i graniczna. Takiej liczby nie da się więc skonstruować z mniejszych "nieskończoności", stosując tylko metody następnikową i sumy!

No dobrze, w takim razie zastanówmy się nad "nieskończonościami", których nie da się skonstruować z mniejszych liczb kardynalnych, używając dowolnych z tych trzech metod. Takie hipotetyczne liczby kardynalne (większe od liczności zbioru liczb naturalnych), których nie można osiągnąć z mniejszych liczb, używając metod następnikowej, podzbiorów i sumy, nazywamy silnie nieosiągalnymi.

Czy jednak takie liczby istnieją? Odpowiedź na to pytanie jest podobna, ale może jeszcze bardziej subtelna niż w przypadku hipotezy continuum. Zakładając nawet, że taka liczba istnieje, możemy rozpatrzeć najmniejszą z nich - i zauważmy, że z powodzeniem możemy uprawiać teorię zbiorów i matematykę tylko w ramach zbiorów mniej licznych niż ona. Nigdy wtedy jej nie napotkamy! To, czy ona istnieje, nie będzie miało dla nas wtedy żadnego znaczenia. Doprecyzowanie tego rozumowania prowadzi do dowodu, że z aksjomatów nie da się wykazać, że taka liczba istnieje.

W drugą stronę jest jeszcze trudniej. Da się bowiem udowodnić, że w ramach aksjomatów nie da się udowodnić, że nie da się udowodnić, że taka "nieskończoność" nie istnieje! Gdyby bowiem było to możliwe, dawałoby to dowód niesprzeczności aksjomatów, co przeczyłoby twierdzeniu Gödla o niezupełności (patrz odcinek "Rozmyślania o myślakach"). Istnienie takich "nieskończoności" jest więc jeszcze bardziej ulotne niż istnienie nieskończoności pomiędzy licznością liczb naturalnych a licznością liczb rzeczywistych.

W takim razie wszechświat zbiorów wygląda następująco: najmniejszym zbiorem jest zbiór pusty, potem są coraz większe zbiory skończone, aż w końcu najmniejsza nieskończona liczba kardynalna 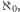czyli liczność zbioru liczb naturalnych. Potem spotkamy zbiory, których liczności to coraz większe "nieskończoności", które możemy skonstruować, poczynając od 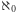i korzystając z metod następnikowej, podzbiorów i sumy. I dalej jest horyzont, za którym być może nic nie ma, a być może jest pierwsza silnie nieosiągalna liczba kardynalna. Z tej "nieskończoności" znów moglibyśmy konstruować coraz większe liczby kardynalne, ale mniejsze niż kolejny hipotetyczny horyzont, którego przekroczyć nie możemy, a który stanowi kolejna silnie nieosiągalna liczba kardynalna. I tak dalej. To jest podróż w nieskończoność i za nieskończoność.

Przygodę tę wypada zakończyć, cytując jednego z bohaterów, od których zaczęliśmy nasze rozważania, czyli Davida Hilberta. "Nieskończoność! Żadne inne pytanie nie poruszyło tak głęboko duszy człowieka".